Adsorption:
Desorption:
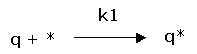
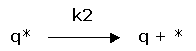
(1) rate of adsorption: ![]()
(2) rate of desorption: ![]()
LANGMUIR-ADSORPTION
Introduction
Whenever a gas is in contact with a solid there will be an equilibrium established between the molecules in the gasphase and the corresponding adsorbed species (molecules or atoms) which are bound to the surface of the solid.
The Langmuir isotherm was developed by Irving Langmuir in 1916 to describe the dependence of the surface coverage of an adsorbed gas on the pressure of the gas above the surface at a fixed temperature. There are many other types of isotherm (Temkin, Freundlich ...) which differ in one or more of the assumptions made in deriving the expression for the surface coverage; in particular, or how they treat the surface coverage dependence of the enthalpy of adsorption. Whilst the Langmuir isotherme is one of the simples, it still provides a useful insight into the pressure dependence of the extent of surface adsorption.
The Langmuir isotherm - derivation from equilibrium considerations
The basic idea behind the Langmuir model is the coverage of the surface by a monomolecularic layer. The model approach also assumes that only one gas is being adsorbed. Thus, at constant temperature a part of the surface will be covered with the adsorbed molecule another part not.
Between the free gas and the adsorbed gas a dynamic equilibrium will exist. Per time unit there will be as much molecules adsorbing as there will be desorbing. The rate of adsorption will be proportional with the equilibrium pressure of the gas and the free surface.
In mathematical terms we derive the following model.
| q = molecule |
* = adsorption site |
q* = adsorbed molecule |
|
Adsorption: |
Desorption: |
|
|
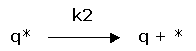 |
|
(1) rate of adsorption: |
(2) rate of desorption: |
(1) + (2)
|
With: |
Total number of adsorption sites: ![]()
|
Load factor or coverage or sorption capacity (3):
|
Combining (3) and (4)
|
|
Applying the ideal gas law and assuming a Gas-Solid system (4):
(C is concentration) |
|
|
|
|
|
|
|
|
Criticism
The main problems with the model can be summarized as follows:
The influence of the temperature on the adsorption equilibrium.
If we assume that the energy and the entropy of the lattice do not change significantly during adsorption than we can state that when a molecule is adsorbed the entropy will decrease, deltaS will be negative and therefore deltaH will be negative.
|
Applying some thermodynamics
|
Arrhenius: |
|
|
|
|
|
|
|
|
|
|
|
||
At a given pressure the extent of adsorption is determined by the value of K: this in turn is dependent upon both the theperature (T) and the enthalpy (heat) of adsorption. The magnitude of adsorption ethalpy reflects the strengthn of binding of the adsorbate to the substrate.
K is increased by:
At higher temperature K reduces which means the surface becomes depopulated.
Chemisorption and Physisorption
With physical adsorption (physisorption) there is only an increase in surface concentration during adsorption. Only van der Waals forces play a role. The heat of adsorption is about 1-10 kcal/mole adsorbed gas.
With chemical adsorption (chemisorption) the heat of adsorption is anout 20-200 kcal/mole adsorbed gas. A chemical bond is formed between the molecule and the surface.
Not only the heat of adsorption but also the the activation energy of the adsorption process is higher with chemisorption than with physisorption. As a consequence physisorption is prelavent at lower temperatures and chemisorption at higher temperatures.
11/03/2002