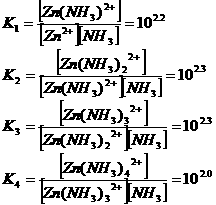
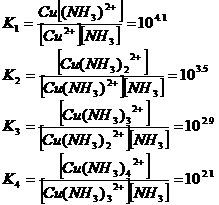
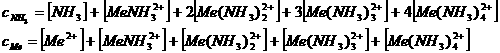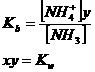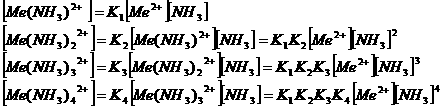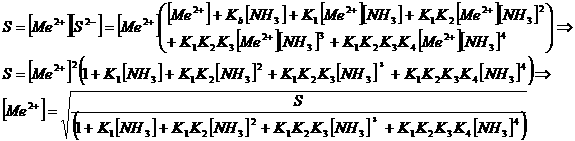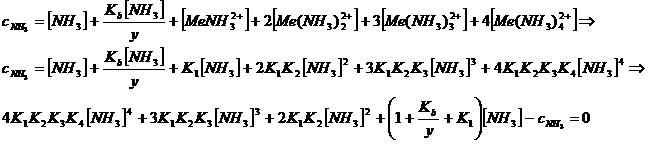Metal sulphides and
ammonia
Reaction
scheme:
(Me =
Metal, Cu or Zn)
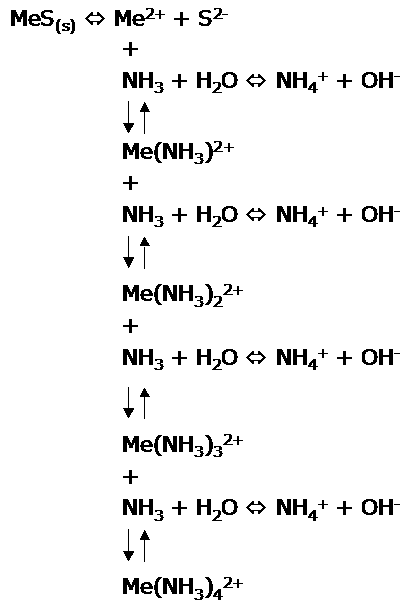
Precipitation:
The
equilibrium reaction for an insoluble salt MZ is:
(MZ)s
ó M+ + Z-
At
equilibrium:
![]()
For a solid
a=1 therefore:
![]()
The product
of the activities of ions in a saturated solution is constant at a given
temperatrure. This constant is called L (Löslichkeitsprodukt) or S (solubility
product). For an ideal solution we can replace activities with concentrations:
S = [M+][Z-]
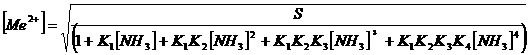
Unfortunately,
solving such a polynomial equation analytically is rather complicated. However,
this problem can be circumvented by employing goalseek in excel.
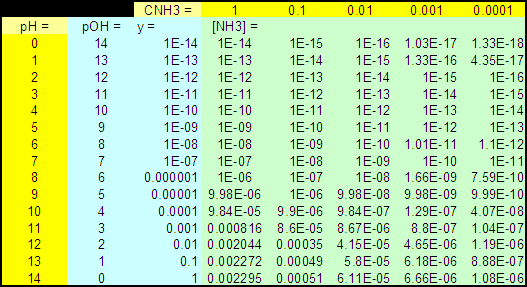
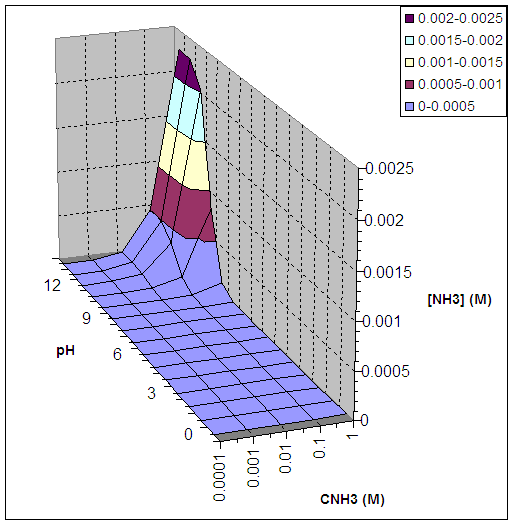
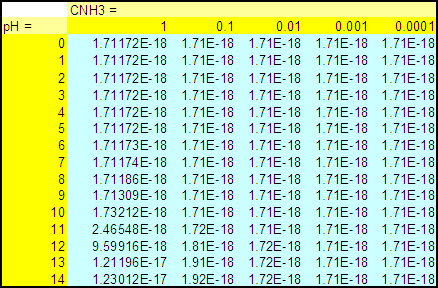
Table 1 : [NH3] as a function of CNH3
and pH for ZnS
(all concentrations in M)
Figure 1 : [NH3] as a function of CNH3
and pH for ZnS
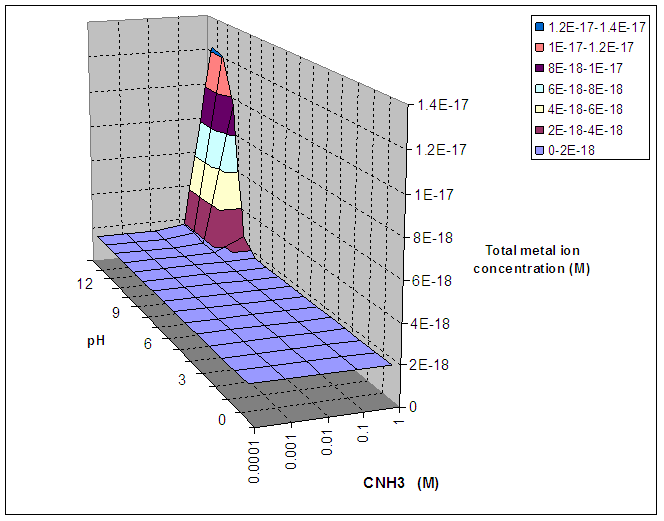
Table 2 : Total Metal
ion concentration as a function of CNH3 and pH for ZnS
(all concentrations in M)
Figure 2 : Total Metal ion concentration as a function
of CNH3 and pH for ZnS