

| Reactorkunde en kinetiek |  |
 |
|
In de reactorkunde hebben we
met de behoudswetten te maken, meer specifiek de wet van behoud van massa. Voor de stofbalans geldt dan in
woorden: (de toename per tijdseenheid
van de massa van een open systeem) = (massadebiet instroom) Ė (massadebiet
uitstroom) In formule:
Op grond van de deze wet van
behoud van massa kan men voor individuele componenten een component balans
opstellen. In woorden: Kortweg: Accumulatie = Input
Ė Output + Productie
Een massa balans kunnen we in
een mol balans omzetten door te delen door te delen door de molmassa van A.
FA is de mol flux We hebben in het experiment te
maken met een zgn batch reactor, een afgesloten systeem met constant volume,
hetgeen betekent dat er geen invoer of uitvoer plaatsvindt:
Om de reactiesnelheidsterm RA
te beschrijven maken we gebruik van de reactiekinetiek. Ra=-kCaaCbb
(mol/(m3.s)) Als a = b = 1:
1ste orde in A en 1ste orde in B, overall een 2de
orde reactie.
Aangezien V constant is:
Hetgeen voor een 1ste
orde reactie in een batchreactor betekent:
Analoog kunnen we afleiden dat
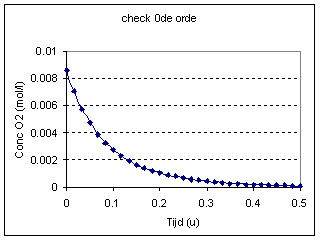
voor een irreversibele 0de orde reactie geldt:
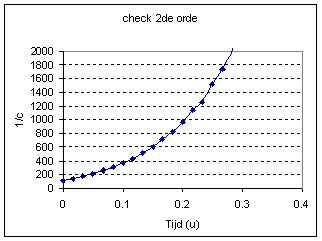
En dat voor een irreversibele 2de
orde reactie geldt:
Door nu steeds deze relaties
grafisch uit te zetten en kijken of deze een rechte lijn opleveren kunnen we
bepalen met welke reactieorde we te maken hebben. Men spreekt dan van de
integrale methode. De reactiesnelheidsconstante k
is geen echte constante maar is wel onafhankelijk van de concentratie van de
reagerende componenten. Men refereert ook wel naar deze constante als de zgn.
specifiek reactie snelheid (s constante). Deze
constante is altijd sterk afhankelijk van de temperatuur. In gas fase reacties
is deze ook nog afhankelijk van de
katalysator en eventueel van de totaaldruk. Volgens Arrhenius wordt de
temperatuurafhankelijkheid van de reactie weergeven door de zgn Arrhenius
vergelijking:
Waarin: Om de Arrhenius vergelijking te kunnen gebruiken om de reactieconstante te bepalen is het noodzakelijk om het experiment bij verschillende temperaturen uit te voeren. In dit geval hebben we het experiment maar bij een temperatuur uitgevoerd. In een situatie waar de reactie
irreversibel is en de reactiesnelheid afhankelijk is van de concentratie van een
component kunnen we de zgn differentiŽle methode gebruiken waarbij we de
reactie bestuderen als een van de componenten in overmaat aanwezig is. Indien: Aŗ P Dan: Ra=-kCaa Hetgeen we analoog aan
hierboven kunnen omwerken naar:
Door deze vergelijking grafisch
uit te zetten kan men dus de reactiesnelheidsconstante en de orde van de reactie
bepalen. Om dit op een redelijk betrouwbare manier te kunnen doen kan men echter
alleen de initiŽle data gebruiken waarin A nog in overmaat aanwezig is. |
Voorbeeld In gas fase reacties geeft men de compositie term in de snelheidsvergelijking vaak weer in partieeldruk van de reagerende componenten. Voor de analyse kan men deze echter beter in concentraties omzetten. Hiervoor gebruiken we de ideale gaswet (Z~1 voor lucht): PA = CA.R.T P in atm (1 atm = 101.325 kPa), C in mol/l, R = 0.082 l.atm/mol.K, T in K. Passen we dan eerst de integrale methode toe op een experiment dan krijgen we: |
|
 |
 |
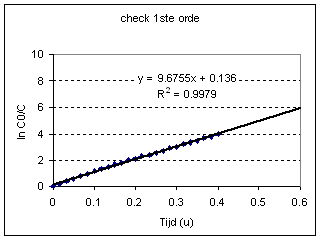 |
De analyse geeft aan de we met
eerste orde kinetiek te maken hebben.
k = e-9.6755 = 6.3.10-5 h-1 = 1.7.10-8 s-1. |
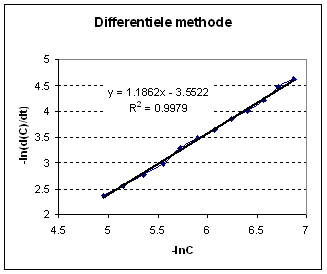 |
Volgens de differentiŽle methode:
De resultaten van de differentiŽle methode wijken sterk of van die verkregen met de integrale methode. Het probleem met de differentiŽle methode is echter dat die alleen maar toepasbaar is wanneer de reactiecondities zodanig zijn dat de snelheid een functie is van de concentratie van slechts een reactant (Hier: O2). |
Literatuur:
Relevante websites:
27-05-2006