Slinger beweging bepalen met de Vernier Motion Detector

Datum: Februari 2018

Inleiding:

Ik heb de Motion Detector samen met mijn CMA Coachlab gekocht maar er eigenlijk te weinig mee gedaan. Dit is een van  mijn pogingen om dat een beetje recht te trekken. 

Principe:

M.b.v. een slinger, een motion detector en Vernier Labquest voeren we de slingerproef uit waaruit we dan de waarde van g bepalen.

Materiaal:

 
  • Vernier Motion Detector
  • Vernier Labquest 2 (of CMA CoachLab)
  • Statief
  • Bal (ca. 13 cm diameter)
  • Paperclip
  • Tang
  • Balans
  • Koorden met verschillende lengtes
  • Liniaal / meetlint
  • Hot-Glue pistool met Hot-Glue
  • PC met Excel (dataanalyse) en Logger Lite of CoachLab.

 

Opstelling & uitvoering:

  • Buig een paperclip om tot een haak en lijm deze vast in de bal zodanig dat deze gemakkelijk opgehangen kan worden.
  • Bepaal de massa van de bal door deze te wegen.
  • Bouw het statief op met een koord en hang de bal op aan het koord.
  • Bepaal de de lengte van het koord.
  • Verbindt de motion detector met de Labquest.
  • Plaats de motion detector op ongeveer dezelfde hoogte als de bal en op een afstand van ongeveer 60 cm.
  • Start de LabQuest op en ga naar het scherm waar men duur en sampling tijd kan instellen.
  • In dit geval een meting van 10 seconden met 20 metingen per seconde.
  • Noteer in het Note veld de lengte van het koord en de massa van de bal.
  • Trek de bal ca. 15 cm van zijn evenwichtspositie en laat los.
  • Start de meting.
  • Sla de meetresultaten op.
  • Herhaal het experiment en herhaal het ook met een langer koord.
  • Exporteer de meting en naar een USB stick.
  • Steek deze in een PC en kopieer de metingen naar de PC.
  • Open de metingen met Logger Lite.
  • Exporteer evt. naar Excel voor verdere verwerking.

Op de bovenste foto ziet men de positionering van de motion detector bij het lange koord.

Lange slinger Korte slinger

Resultaten:
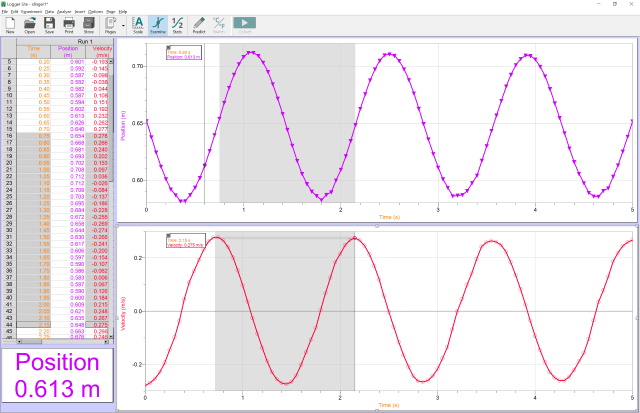
In onderstaand screenshots kan men de resultaten van experimenten zien geďmporteerd in Logger Lite. Zoals men kan zien worden afstand en snelheid gerapporteerd. Op de tijdsas kan men m.b.v. de tabel de trillingstijd bepalen.
Experiment 1:

Massa bal: 140 g ; Koordlengte 1: 42 cm.; T = 2.15 -0.75 = 1.4 s
Experiment 2
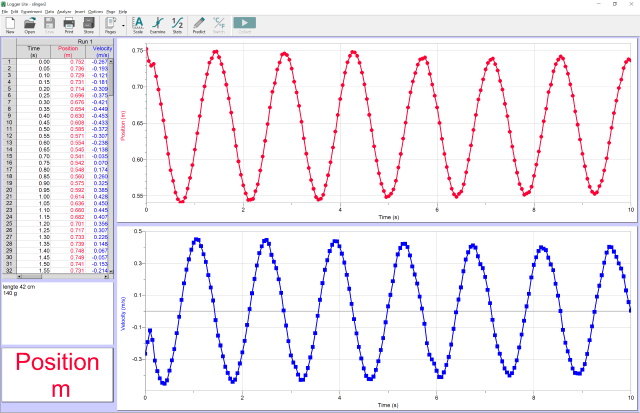Massa bal: 140 g ; Koordlengte 1: 42 cm.; T = 3.85 -2.50 = 1.35 s
Experiment 3
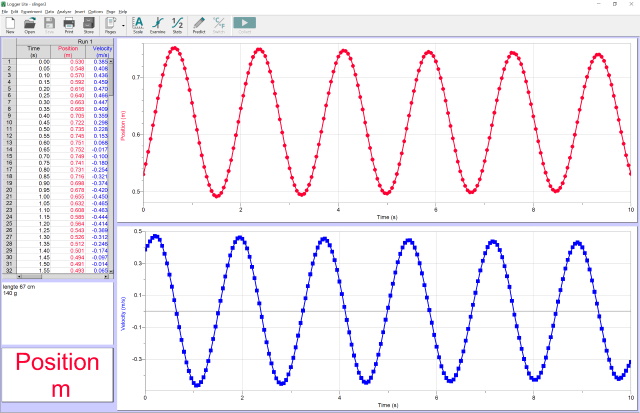Massa bal: 140 g ; Koordlengte 1: 67 cm.; T = 5.4 -307 = 1.7 s
Experiment 4
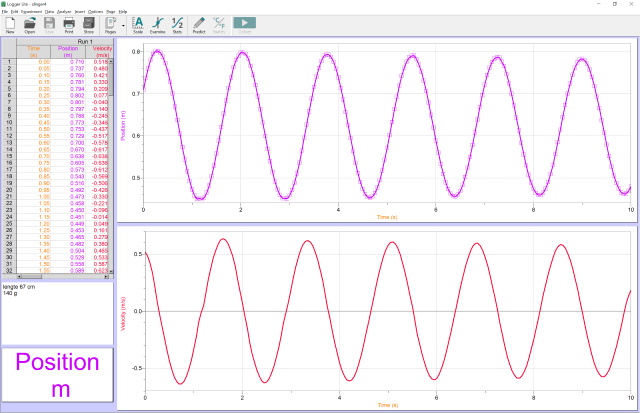Massa bal: 140 g ; Koordlengte 1: 67 cm.; T = 5.05 -3.35 = 1.7 s
Experiment 5
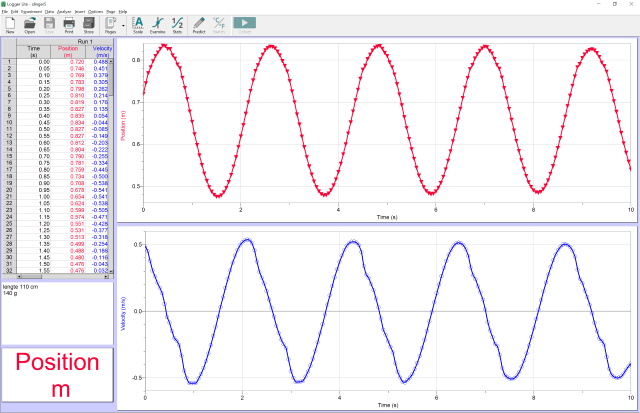Massa bal: 140 g ; Koordlengte 1: 110 cm.; T = 6.4 -4.3 = 2.1 s
Experiment 6
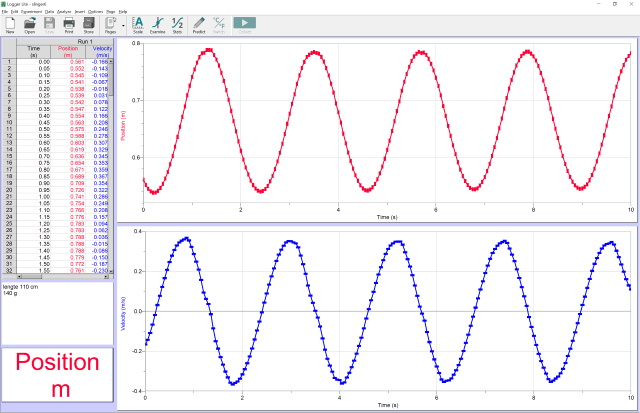Massa bal: 140 g ; Koordlengte 1: 110 cm.; T = 7.4 -5.2 = 2.2 s
Men kan de data ook exporteren als een text file en deze importeren in Excel waarna men er wat berekeningen op kan uitvoeren. De versnelling kan op deze manier ook zichtbaar genaakt worden (rode lijn).
Excel import
 
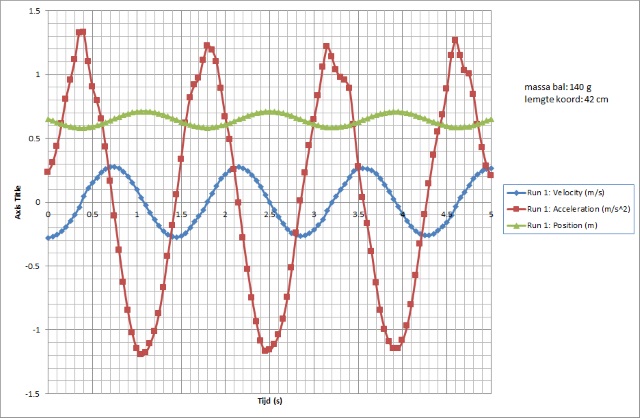De verzamelde meetgegevens zijn samengevat in onderstaande tabel.

Op basis waarvan onderstaande grafiek gemaakt is.
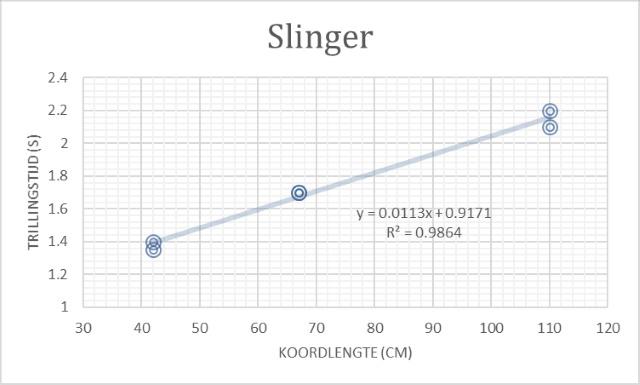Deze laat zien dat bij een constante massa de trillingstijd bepaald wordt door de koordlengte. De trillingstijd neemt toe als de lengte toeneemt.
 

Discussie:

Zolang de uitwijking niet te groot is benaderde de slingerbeweging een eenvoudige harmonische oscillatie en produceert een sinusoidaal patroon. In dit experiment gebruiken we de  Motion Detector om de positie van de slinger te bepalen als functie van de tijd.

 
Al met al is dit een vereenvoudigde slingerproef. Een van de variabelen die ik niet veranderd heb is de massa van de bal. Dat was min of meer afgedwongen omdat ik maar 1 bal van deze grootte in mijn bezit had. Een andere variable is de hoek waaronder me  de slingerbeweging begint.
 

Conclusies:

  • Voor een slinger met constante massa geldt dat de trillingstijd bepaald wordt door de koordlengte. De trillingstijd neemt toe als de lengte toeneemt.

Literatuur:

 
  • T.H. Savory; Natuurkunde Thuis; Thieme; 2de druk; p. 25-30.
  • Keith Caly; 'The Pendulum, Gravity, and that Number “9.8”' ; The Physics Teacher; 42  January 2004; p. 14,15.
  • Dr. J. Schweers en Drs. P. van Vianen; Natuurkunde op copusculaire grondslag - Deel drie voor de bovenbouw van het vhmo; Malmberg; 12de druk; 1964; p.1986, 1987. 
  • Raymond A. Serway and Jerry S. Faughn; College Physics; Thomson; 6th Ed; 2003; ISBN 0030351146; p. 402-406.
  • Niek de Kort; Klassieke Mechanica; Teleac; 1989; ISBN 9065332081; p.190-192.
  • Richard T. Weitner and Robert L. Sells; Elementary Classical Physics Volume 1; Allyn And Bacon; 2nd Ed.; 1973 (1965); ISBN 020503587; p. 270,271

Relevante websites:

Minder relevante websites:

Opmerkingen:

  • Een Labquest 2 is natuurlijk niet essentieel. Elke andere datalogger met de mogelijkheid een ultrasone afstandsmeter aan te hangen, zoals de CMA CoachLab, voldoet ook. Men kan dit experiment ook uitvoeren met Arduino of Raspberry Pi en een ultrasoon module.
  • Deze motion detector is een wat ouder model hetgeen betekent dat ik een afstand van ca. 60 cm moet aanhouden en het object niet te klein mag zijn.
  • Logger Lite kan men gratis downloaden van de Vernier website. Van CoachLab kan men ook een Lite versie downloaden.

Achtergrondinformatie:

In onderstaande figuur is op een geďdealiseerde manier een eenvoudige slingerbeweging weergegeven: men puntmassa m hangt aan een massaloos koord met lengte l.

We geven de slinger een uitwijkingshoek a tov van de verticale ruststand hetgeen betekent dat de massa een booglengte aL van de evenwichtspositie afraakt. De zwaartekracht zorgt er nu voor dat deze massa weer terugkeert naar de evenwichtspositie.  De kracht die uitgeoefend wordt kunnen we ontleden in twee componenten waarvan er een loodrecht op het koord staat, de grootte van die kracht is -mg.sina. De versnelling van de afgelegde weg is gelijk aan de 2deafgeleide van de verplaatste booglengte. 

Langs de boog gezien geldt de 2de wet van Newton: ma=F, dus:

 
Deze vergelijking is niet de vergelijking voor een eenvoudige harmonische beweging. De 2deafgeleiden van de verplaatsing (de hoek a) is niet evenredig met –a maar met –sina.

De hierboven afgeleide dv kent geen eenvoudige oplossing maar door gebruik te maken dat voor kleine hoeken van a geldt dat deze gelijk is aan de sinus kunnen we hem hanteerbaarder maken.

Indien a dusdanig klein is dat sina ~a geldt:

Dit is de algemene dv voor een harmonische oscillator met als  oplossing:

  

Waarbij a0 de uitwijking is die bij de start geldt. 
Voor de hoekfrequentie geldt:

Waardoor voor de trillingstijd geldt dat:  

De slingertijd wordt dus bepaald door de lengte van het koord aangezien g op aarde nagenoeg constant is.
De slingertijd is de tijdsduur die verloopt tussen twee momenten waarop een punt (bijvoorbeeld de massa) van een slinger zich weer op hetzelfde uiteinde bevindt. 

De slingertijd wordt ook wel periode genoemd.

Uit de formule van de slingertijd kunnen we afleiden dat de periode van een slinger alleen maar afhankelijk is van de lengte van de slinger en de gravitatieconstante. Ook speelt de amplitudo niet een bijzonder grote rol zolang deze relatief klein is (sinusbenadering moet blijven gelden). Deze afhankelijkheid maakt het mogelijk de slinger als klok te gebruiken. 

Galileo was de eerste die opmerkte dat de periode van een slinger onafhankelijk is van zijn amplitudo. 

Geologen maken gebruik van een slinger als ze op zoek zijn naar olie en mineralen. Afzetting beneden het oppervlak van de aarde kunnen afwijkingen in de gravitatieconstante veroorzaken. Door gebruik te maken van een speciaal ontworpen slinger van bekende lengte wordt de periode gemeten, die dan weer gebruikt wordt om g te berekenen

24/03/2020