De Wet van Ohm
met CoachLab

Datum: April 2021

Inleiding:

Een experiment dat ik al eerder heb uitgevoerd maar dat ik mop een iets andere manier kon uitvoeren.

Principe:

M.b.v. een rheostaat, een voedingsbron, een voltmeter en een ampère meter laten we zien dat de wet van Ohm nog steeds klopt.

Materiaal:

 
  • Rheostaat
  • CMA Coachlab
  • Batterij 9V
  • Vernier Stroomsterkte Sensor
  • Vernier Spannings Sensor
  • Kabels
  • PC met Excel (data-analyse) en Logger Lite
  • Multimeter
  • Koolweerstanden
    - 4 Ohm
    - 15 Ohm
    - 23 Ohm
    - 34 Ohm

Rheostaat

CMA Coachlab
Stroomsterkte sensor

Spannings sensor

Opstelling & uitvoering:
  • Gebuik de multimeter om de weerstandwaarden van de koolweerstanden te meten.
  • Bouw de schakeling op zoals weergegeven in nevenstaand schema en in onderstaande foto.
  • Let erop dat de voedingsbron uitstaat.
  • Verbindt de Stroom Sensor met Kanaal 1 en de Spanningssensor met Kanaal 2 van de CMA Coachlab.
  • Start Coachlab op de PC op.
  • Deze laat de meetwaardes van de sensoren zien.
  • Bouw het Coachlab scherm op zoals in onderstaande screenshot te zien is.
  • Een grafiek met op de x-as de potentiaal (V) en op de ij-as de stroomsterkte (A)
  • Start een meting
  • Beweeg de rheostaat op en neer
  • Stop de meting
  • Voer een analyse uit binnen Coachlab. Bepaal een best fit lineaire relatie
  • Exporteer eventueel de data als CSV file voor analyse in Excel.
Resultaten:

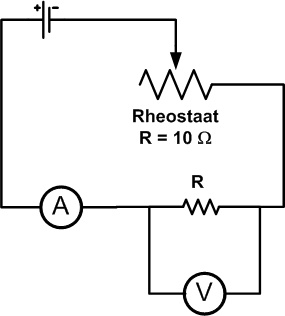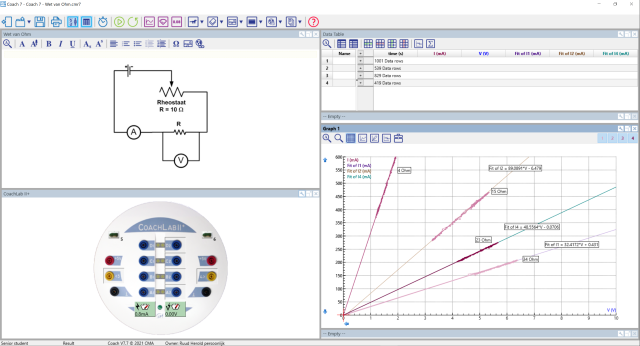De grafiek uitvergroot

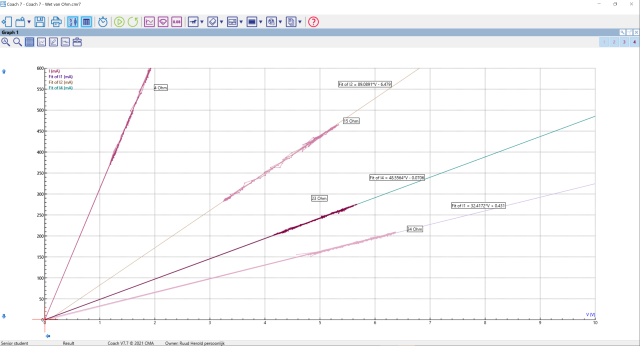Discussie:

In de uitgevoerde experimenten kunnen we een lineaire relatie waarnemen tussen de spanning en de stroomsterkte die over een weerstand gemeten is. Waar we echter nu al even aan moeten denken is dat we meten over de koolweerstand, die constant is en we de variatie creëren door de weerstand van de rheostaat te veranderen. We varieren dus de weerstand van de rheostaat (1 - 2 Ohm) en meten het voltage over de koolweerstand.
Wat we nu in de grafiek zien kunnen we uitleggen m.b.v. nevenstaand schema. De spanning over het hele circuit is constant (batterij 9 V). Deze spanning verdeeld zich over de rheostaat en de weerstand. In formule:
U = U1 + U2

Als we de rheostaat op en neer bewegen veranderd de weerstand van de rheostaat (Rv) . Aangezien we hier met een serieschakeling te maken hebben geldt ook:
R = R1 + Rv

Veranderen we nu Rv (de rheostaat) dan veranderd R dus ook en in de grafiek kunnen we zien dat dan zowel U als I veranderen.

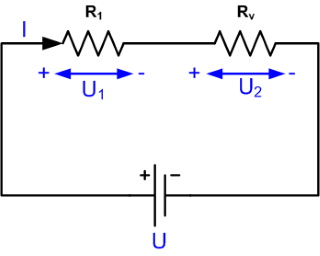Aangezien U constant is veranderd alleen maar de verdeling van U over R1 (U1) en Rv (U2). Als Rv afneemt zals de spanningsval (U2) over Rv afnemen en de spanningsval (U1) over R1 toenemen. In de grafiek kunnen we zien dat als U1 groter wordt de stroomsterkte I ook groter wordt en vice versa. De geïnterpoleerde lijn gaat nagenoeg door 0 en dat impliceert dat er een lineaire relatie is tussen U en I als R veranderd.

De observatie dat de lijnen niet exact door 0 gaan kunnen we toeschrijven aan de invloed van meetfouten.

Iets formeler geformuleerd:
Men kan dan concluderen dat de spanning U (in V) over een elektrische component varieert samen met de stroomsterkte I (in A) volgens een vaste relatie: U = I * R.
Hierin is R (in Ohm) de weerstand van deze elektrische component (rheostaat + koolweerstand).

Conclusie:

  • De spanning U "(in V) over een elektrische component varieert samen met de stroomsterkte I (in A) volgens een vaste relatie: U = I * R Hierin is R (in Ohm) de weerstand van deze elektrische component.

Literatuur:

  • R.J. Flink; "Elektriciteitsleer"; Nijgh & Van Ditmar; 1ste druk; 1992; ISBN 902360673; p. 6-13. 
  • Raymond A. Serway and Jerry S. Faughn; "College Physics"; Thomson; 6th Ed; 2003; ISBN 0030351146; p. 536, 537.
  • Richard T. Weitner and Robert L. Sells; Elementary Classical Physics Volume 2; Allyn And Bacon; 2nd Ed.; 1973 (1965); ISBN 020503598; p. 541-548.
Relevante websites: Minder relevante websites:

Opmerkingen:

  • De Coachlabfile die ik gebruikt heb: Wet van Ohm.cmr7
  • Ohm voerde deze experimenten uit met een draad. De Rheostaat is in feite ook een draad, alleen zit deze opgerold.
  • Van de Wet van Ohm kan men dan weer gebruik maken door m.b.v. een U, I meting de weerstandswaarde van een onbekende weerstand te bepalen.

Achtergrondinformatie:

De fundamentele relatie tussen stroom, spanning en weerstand is ontdekt door Georg Simon Ohm. Om zijn bijdrage te eren is de eenheid van elektrische weerstand naar hem genoemd.

De Duitse natuurkundige George Simon Ohm (1789-1854) werd geboren in Erlngen. Ohm toonde in 1826 aan, dat de stroomsterkte in een draad rechtevenredig is met de aangelegde spanning en omgekeerd evenredig is met de weerstand van een draad.  George Ohm verrichtte ook baanbrekend werk op het gebied van de akoestiek. Vanaf 1833 werkte George Ohm in Neurenberg en in 1850 werd hij tot professor benoemd in München. In 1854 overleed Ohm te München.
 

De Ohm (symbool: Ω, de Griekse hoofdletter omega) is de afgeleide SI-eenheid voor elektrische weerstand. De ohm is de elektrische weerstand tussen twee punten van een homogene geleider als bij een constant potentiaalverschil van 1 volt tussen die punten een constante stroom van 1 ampère ontstaat. Uitgedrukt in SI-eenheden: 1 Ω = 1 kgm2A−2s−3.