Geluidssnelheid in een metalen pijp

Datum: November 2009

Inleiding:

Een van de experimenten die je leest en waarvan je denkt dat moet ik zelf ook eens proberen.

Principe:

M.b.v. microfoons, een geluidskaart, sotware en een metalen pijp de geluidssnelheid bepalen.

Materiaal:

  • Microfoons met eigen voeding
  • Metalen pijp van 2 m
  • PC met geluidskaart
  • MacScope Software
  • Tape
  • Y-combineerstekker of kabel
  • Hamer
     

 

De MacScope software kan men gratis downloaden van: Physics2000 MacScope

Voor dit experiment is het van belang dat men een microfoon gebruikt met zijn eigen stroomvoorziening. Nevenstaande microfoon heb ik bij Mediamarkt gekocht voor € 19. Deze heeft een aan/uit knop en gebruikt een knoopcel als voeding.

 

Experimententele opstelling:

  • Tape de microfoons vast op de uiteinden van de buis.

  • Steek de stekkers in het Y-koppelstuk en deze vervolgens in de microfooningang van de computer.

  • Zet de microfoons aan.

  • Start op de PC het MacScope programma en stel dit in op trigger mode.

  • Sla met de hamer op een uiteinde van de buis.

  • Analyseer het verkregen signaal.


 

Uitvoering en resultaten:

Van belang is om zich te realiseren dat als men maar een microfoon men te maken krijgt men een signaal dat aan het andere uiteinde gereflecteerd wordt. De effectieve weglengte is dan 4 m. Het resultaat van een zulk experiment is weergegeven in onderstaande figuur.
Met behulp van MacScope kan men de periode van een aantal trillingen bepalen, zoals weergegeven in onderstaande figuur.

5.58 ms voor 8 trillingen komt overeen met 0.6975 ms/trilling.
Dit geeft een geluidssnelheid van 4/0.0006975 = 5735 m/s.
Ik heb dit experiment vervolgens nog twee maal herhaald.

7.79 ms voor 11 trillingen komt overeen met een geluidssnelheid van 5648 m/s.

7.84 ms voor 11 trillingen komt overeen met een geluidssnelheid van 5612 m/s.
Gemiddeld vinden we dan een geluidssnelheid van 5665 m/s.
In de literatuur vinden we voor staal waardes in de range 5000 - 6000 m/s hetgeen betekent dat we een reële waarde gevonden hebben.
 
Volgens het artikel van Huggins, dat we volgen, moet het mogelijk zijn m.b.v. trigger instellingen met beide microfoons tegelijk te meten aangezien we een stereo signaal als input hebben. De effectieve weglengte is dan 2 m.
 
Indien men beide microfoons gebruikt kan men het signaal aan beide kanten meten en is de effectieve weglengte 2 m. Een zulk experiment is in onderstaande screenshot weergegeven.

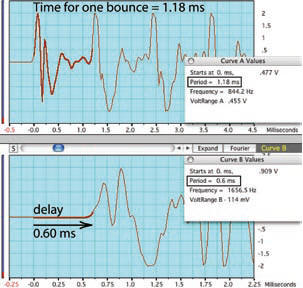
In eerste instantie lijkt het erop dat er tussen beide signalen een klein verschil is, hetgeen we ook verwachten. Het verschil is ca. 3.5 hokjes. 1 hokje komt overeen met 0.25 ms. De totale vertraging is dan .875 ms. Dit komt overeen met een geluidssnelheid van 2/(0.875/1000) = 2286 m/s. Hetgeen een veel te lage waarde is. Kijken we nog eens wat nauwkeuriger naar het signaal dan zien we dat beide tijdsassen niet corresponderen. Synchroniseren we deze dan zien we geen enkel verschil op de tijdas.

Deze observatie komt dus niet overeen met wat in het artikel beweerd wordt. Ik heb dit experiment nog vele malen herhaald maar het is me niet gelukt om dezelfde observatie te doen als in het artikel van Huggins getoond wordt, ook niet als we het experiment uitvoeren op een andere computer. Het in het artikel getoonde resultaat is weergegeven in nevenstaande figuur.

Ik heb ook nog het experiment proberen uit te voeren op de manier zoals door Potter wordt beschreven, door koperdraad om een uiteinde te winden en dat te verbinden met een oscilloscoop en vervolgens met een hamer op het andere uiteinde te slaan. De oscilloscoop pikte echter geen signaal op. Mogelijk dat ik te weinig windingen had (Potter gebruikte 2500 windingen).
Al met al kan ik dit experiment maar als gedeeltelijk geslaagd beschouwen.

Discussie en conclusie:

De geluidssnelheid in een bepaald medium is de snelheid waarmee geluidstrillingen of geluidsgolven zich voortplanten door dat medium. Deze snelheid wordt bepaald door de vastheid en samenstelling van dat medium en door de temperatuur. Voor lucht en bij kamertemperatuur is de geluidssnelheid ca. 340 meter per seconde, in vloeistoffen en vaste stoffen is de geluidssnelheid meestal hoger. In water bijvoorbeeld plant geluid zich voort met een snelheid van ca. 1500 m/s en in pstaal ca. 5800 m/s. Bij de hardste metalen kan de geluidssnelheid oplopen tot 43.000 km/u. De geluidssnelheid is afhankelijk van de natuurlijke elasticiteit van de moleculen waaruit het medium bestaat.
Longitudinale golven die kunnen optreden in een staaf hebben een voorplantingssnelheid van:
c_{\mathrm{solids}} = \sqrt{\frac{E}{\rho}}

waarin

E = Young's modulus ook wel elasticiteitsmodulus genoemd.
ρ (rho) = dichtheid

Voor staal, gebruik makende van een typische waarde voor staal krijgt men dan:

$\displaystyle c = \sqrt{ E \over \rho} = \sqrt{160 \times 10^{9} N/m^{2} \over 7860 Kg /m^3} = 4512 m/s$

Hte is echter van belang zich te realiseren dat er twee verschillende snelheden zijn waarmee geluiid zich door staal verplaatste. De longitudinale trillingen (druk golven, het medium vibreert in de richting van de acoestische golf) verplaatsen zich met een snelheid van ca. 6000 m/s terwijl de transversale golven (shear golven, het medium vibreert onder een rechte hoek t.o.v. de bewegingsrichting) zich verplaatsen met een snelheid van ca.3000 m/s.

Samengevat:
Materiaal Referentie Waarde [m/s] 
Staal
 
longitudinale golf 
5790
 
Staal
 
transversale shear
 
3100
 
Staal
 
longitudinale golf (extensionale golf)
 
5000

Conclusie:

De gemeten geluidsnelheid in een rvs pijp is: 5665 m/s

 

Literatuur:

  • Elisha Huggins;'Speed of Sound in Metal Pipes: An Inexpensive Lab'; The Physics Teacher; 46 January 2008; p. 13,14.
  • Earl D. Blodgett;'Comments on Speed of Sound in Metal Pipes: An Inexpensive Lab'; The Physics Teacher; 47 January 2009; p. 31,32.
  • David Potter;'The Speed of Sound in an Iron Rod'; The Physics Teacher; 40 January 2002; p.56,57.
  • Karl C. Mamola; 'Measurement of Sound Velocities in Metal Wires'; American Journal of Physics; 42 December 1974; p. 1117,1118
  • Tony Key, Robert Smidrovskis, Milton From; 'Measuring the Speed of Sound in a Solid' The Physics Teacher; 38 February 2000; p.76,77.
  • Gerald P. Hart; 'Measurement of the Speed of Sound in Metal Rods Using the Microcomputer' The Physics Teacher; February 1988; p.89.
  • Michael T. Frank, Edward Kluk;  'Velocity of Sound in Solids' The Physics Teacher; April 1991; p.246-251.
  • C. Fazio, I. Guastella, R.M. Sperandeo-Mineo, G. Tarantion; 'Measuring longitudinal wave speed in solids: two methods and a half'; European Journal of Physics; 27 2006; p. 687-701. 

Relevante websites:

Opmerkingen:

  • De pijp kan men in een bouwmarkt voor een paar euro kopen.
  • Daarnaast is er ook software beschikbaar die ervoor zorgt dat je de geluidskaart in je PC als een oscilloscoop kunt gebruiken (zie: MacScope II).
  • PC microfoons of soortgelijke microfoons zonder eigen voeding werken niet. Het enige alternatief dat men dan heeft is een versterkerschakeling met voeding bouwt.

  • Het type microfoon dat ik gebruikt heb is ook verkrijgbaar bij Conrad voor € 20, de condensator revermicrofoon (bestelno. 302591-89). Er is ook een duurdere versie verkrijgbaar (opsteekmicrofoon).

Achtergrondinformatie:

Geluidssnelheid in vaste stoffen

stof snelheid
(m/s)
Aluminium 5080
Been (massief) 3000
Been(poreus) 2600
Beton 4300
Brons 4700
Diamand 12000
Glas 4000-4500
Goud 4700
Hout 3850
Ivoor 3000
Koper 3560
Lood 1322
Lucite 2680
Marmer 3800
Pyrex glas 5640
Rubber 1600
Staal 5100
Steen 6000
Ijs 3280
IJzer 5125
 

13/01/2017