

| Thermometrische en potentiometrische titratie van azijnzuur met natronloog (Coachlab) |  |
 |
Datum : febbruari 2006
Principe:
Het gehalte van azijnzuur (HAc) bepalen d.m.v.
een zuur-base reactie met natronloog.
Het equivalentiepunt bepalen we zowel thermometrisch als potentiometrisch:
De zuur-base reactie: NaOH + HAc --> H2O + Na+ + Ac-
Benodigd:
|
|
Werkwijze:
|
|
|
|
Opstelling |
|
|
|
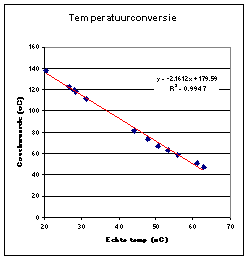
Screenshot Er is een specifiek probleem met de gebruikte software. Men kan n.l. alleen een voorgeprogrammeerde temperatuursensor gebruiken en dat is een andere dan ikzelf tot mijn beschikking had. Dit betekent dat men een ijklijn moet maken om de gemeten temperatuur te converteren naar de werkelijke temperatuur. Hiervoor is een tweede (losse) temperatuursensor nodig. Warm een bekerglaasje met water op en laat het afkoelen. Meet regelmatig de temperatuur met de losse sensor en lees de Coachlab waarde op datzelfde moment uit. Zet deze getallen tegen elkaar uit en gebruik de trendlijn voor de conversie. |
Meetresultaten:
|
Gemeten titratie curves: |
Temperatuur probe ijklijn: |
|
|
 |
De resultaten en berekeningen zijn te vinden in de te downloaden file: HAcNaOH.xls
|
Potentiometrisch |
|
| Berekenen we het
equivalentiepunt mbv de potentiometrische titratie door de differentiaal
methode te gebruiken dan is het equivalentiepunt: 11.74 + (0.4/0.5)*0.01 = 11.748 ml. We hadden ingewogen aan loog: 10.06 g
NaOH Bij een e.p. van 11.748 ml is er 11.748 * 2.514 = 29.53 mmol OH toegevoegd. |
|
| Deze zitten dan
in 27.5 g azijnzuur oplossing, In 100 g azijnzuur oplossing zitten dan 100/27.5 * 29.53 = 107.4 mmol. Het azijnzuurgehalte is dan 107.4*60/1000 = 6.44 wt%
|
|
|
Thermometrisch |
|
|
|
|
| Om het e.p. te
berekenen van de thermometrische titratie kunnen we het beste van excel
gebruik maken. In excel splitsen we de data voor en na het e.p. en trekken
er een trendlijn door heen. Excel geeft ons de vergelijking van de
trendlijn. Om het e.p. te berekenen bepalen we het snijpunt van de lijnen
hetgeen betekent dat we de volgende vergelijking oplossen: 0.4436x
+21.521 = -0.0879x = 27.782 We vinden dan voor het e.p.: x=11.780 ml Het bijbehorende azijnzuurgehalte is: 11.780*2.514*100/27.5*60/1000 = 6.46 wt% |
|
Discussie:
|
We vinden dus met beide methodes nagenoeg hetzelfde resultaat. De grootste onnauwkeurigheid in deze bepaling zit volgens mij in de titer van de loog. De loog is niet gesteld, dus de concentratie kan afwijken van hetgeen we op basis van de weegcijfers verwachten. De potentiometrisch gevonden curve kunnen we relatief gemakkelijk afleiden. Gegevens: |
| Ac = acetaat HAc = azijnzuur |
pKa = 4.7 c = concentratie HAc (M) |
x = [H3O+] y = [OH-] |
|
Reaktievergelijkingen: De reactie van azijnzuur (HAc, formule: CH3COOH) met natronloog kunnen we als volgt uitschrijven: |
||
| 1. | Evenwichtsdissociatie van azijnzuur: | HAc + H2O <=> Ac- + H3O+ |
| 2. | Dissociatie van NaOH: | NaOH -> Na+ + OH- |
| 3. | Neutralisatiereaktie: | H3O+ + OH- <=> 2H2O |
| Bruto reaktievergelijking: HAc + NaOH <=> Ac- + Na+ + H2O | ||
| Vergelijkingen: |
| (1) | c = [HAc] + [Ac-] => [HAc] = c - [Ac-] |
| (2) | |
| (3) |
elektroneutraliteitsvergelijking: [Ac-] + y = x + [Na+] |
| De elektroneutraliteitsvergelijking is het uitgangspunt van de berekeningen. |
| (1) + (2) | (4) | |
| (4) in (3) | (5) |
|
Onder de omzettingsgraad l verstaan we de toegevoegde hoeveelheid reagens in mol gedeeld door de te bepalen hoeveelheid stof in mol. Voor de titratie van een eenwaardig zuur met een eenwaardige base ligt het equivalentiepunt dus bij l =1. Bij de nu volgende theoretische afleiding van de titratiecurve wordt de aanname gemaakt dat het volume tijdens de titratie niet verandert. Dus: |
| (6) | ||
| (6) in (5) | (7) |
|
M.b.v. excel is eenvoudig een tabel samen te stellen die de
l
bij verschillende pH's uitrekent. Uiteraard kan deze tabel weer gebruikt
worden om de titratiecurve te tekenen. Nog makkelijker is het om bij een gegeven
pH de
l
te berekenen en deze
l
vervolgens
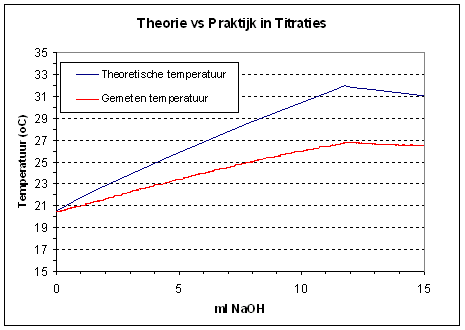
om te rekenen naar ml NaOH. Vergelijken we nu theorie met praktijk dan krijgen we onderstaande grafiek. |
|
|
|
Het verschil tussen theorie en praktijk in de
potentiometrische titratie te verklaren is iets
complexer. In het hoge pH gebied laat de invloed van CO2 zich
merken. In het lage pH gebied is dat iets complexer. Een van de zaken
waar we niet voor corrigeren is het verdunningseffect dat optreedt als we
reagens toevoegen. Dit effect is echter niet groot, waarschijnlijk speelt de
onnauwkeurigheid die we in de titer van het NaOH hebben een grotere rol.
|
|
Ook over de thermometrische titratiecurve kunnen we een en ander vertellen.
Een neutralisatie reactie is endotherm, de temperatuur van de oplossing neemt toe totdat het equivalentiepunt bereikt is. Als we na het equivalentiepunt titrant blijven toevoegen dan vindt er geen neutralisatiereactie meer plaats en produceren we geen warmte meer. We voegen echter wel een "koude" titrant aan een "warme" oplossing toe waardoor deze in temperatuur zal gaan dalen. Door vervolgens een grafiek uit te zetten van de temperatuur tegen het volume toegevoegde titrant kunnen we het equivalentiepunt bepalen door het snijpunt van de verwarmingscurve en de afkoelingslijn te berekenen. |
| Ook theoretisch
kunnen we dit verder onderbouwen:
De temperatuurstijging voor het equivalentiepunt kunnen we berekenen m.b.v. de formule:
De temperatuur van de oplossing na het equivalentiepunt kunnen we berekenen m.b.v. de formule:
waarin: M.b.v. de reeds afgeleide titratievergelijking en bovenstaande formules kunnen we een theoretische thermometrische titratiecurve berekenen. |
|
| Vergelijken we nu
de berekende curve met de gemeten curve dan valt ons onmidellijk op dat de
gemeten curve onder de berekende curve valt. Op zich is dat makkelijk te
verklaren. In onze theoretische benadering hebben we geen rekening gehouden
met warmteverlies naar de omgeving hetgeen in werkelijkheid wel plaats
vindt. We hebben zelfs niet bijzonder ons best gedaan om dit warmteverlies
te beperken door de titratie in een ge´soleerd vaatje uit te voeren. De
warmte die we in het systeem stoppen door constant te roeren kan dit
warmteverlies niet tegengaan.
Volgens Mahoney et al is er nog een tweede manier om de thermometrische curve te berekenen, die ik echter niet uitgeprobeerd heb. Zij beschrijven een methode waarbij de concentratie van alle ionen wordt uitgerekend waarbij rekening gehouden wordt met de verdunning en het effect van de veranderende ionensterkte van de oplossing op de activiteitscoŰfficiŰnten. Uitgaande van een initieel monster (bv 100 ml 1 M zuur) wordt de totale enthalpie verandering berekend als een 1 M NaOH oplossing wordt toegevoegd door de standaard vormingsenthalpien van de verschillende ionen op te nemen in een gewogen vergelijking: q = S DHof [ni(mengsel) - ni(beginoplossing)] De resultaten worden vervolgens geconverteerd naar een constant variabel format door te schalen naar een constant volume van 100 ml. Ze rapporteren dat op deze manier de maximale temperatuurverandering (DTmax) zeer nauwkeurig berekend kan worden. |
Conclusie:
|
Opmerkingen:
|
Literatuur:
Relevante websites: |
Achtergrondinformatie:
| Thermometrische titratie Een thermometrische analyse is in principe een flexibele, eenvoudig uit te voeren analysemethode gebaseerd op een eenvoudig principe, het gebruik maken van de reactieenthalpie, DH, voor de reactie van een titrant met de te bepalen component. Meestal is deze reactie exotherm waardoor de oplossing lichtjes verwarmd wordt als de titrant toegevoegd wordt. Bijna elke reactie kan gebruikt worden voor een thermometrische titratie zolang als de reactie volledig verloopt (evenwicht volledig naar rechts), een "grote" reactieenthalpie heeft en voldoende specifiek is voor de component die bepaald moet worden. In de meeste gevallen resulteert de enthalpieverandering in een temperatuurverandering gedurende de titratie van ca. +/- 3 oC. In goed ge´soleerde reactievaten kan men ook veel kleinere temperatuurveranderingen meten. De reactant of titrant voeren we continue of stapsgewijs toe, hetgeen van belang voor de reproduceerbaarheid. Het titratievat is bij voorkeur dusdanig opgebouwd dat warmteopname van of afgifte naar de omgeving geminimaliseerd is. Daarnaast moet de titratie zo snel mogelijk uitgevoerd worden (< 5 min). Het eindpunt in een thermometrische titratie wordt verkregen uit een plot van de temperatuur van de titreren oplossing als een functie van het volume van het toegevoegde reagens. Voor een succesvolle titratie is het essentieel dat er een verandering is in de vrije energie DGo in het gebied waar het equivalentiepunt zich bevindt. Deze conditie is gebaseerd op de evenwichtconstante van de betrokken reacties. -DGo=RTlnK Een thermometrische titratie is echter afhankelijk van de reactiewarmte volgens de relatie: DH = DG + T.DS Een thermometrische titratie is haalbaar als er een significante verandering in de entropie term (DS) plaatsvindt (vooropgesteld dat de veranderingen in vrije energie dit mogelijk maken) waardoor een voldoende grote "totaal" verandering in de enthalpie (DH) plaatsvindt. Een potentiometrische van een zwak zuur (bv boorzuur) met NaOH levert een zeer zwak eindpunt op terwijl een thermometrische titratie van boorzuur met NaOH een duidelijk eindpunt oplevert. De verandering in temperatuur (DT) van een zuur-base reactie is afhankelijk van de molaire neutralisatiewarmte (DHm) en wordt weergegeven door de relatie: DT = N.DHm/Cs waar N het aantal mol water representeert dat door de neutralisatiereactie gevormd wordt en Cs de warmtecapaciteit weergeeft. Aangezien DHm en Cs constant zijn gedurende de titratie is DT proportioneel tot N. De neutralisatiewarmte bij de tiratie van een sterk zuur met een sterke base wordt geheel bepaald door de vorming van water terwijl bij de titratie van een zwak zuur het dissociatie-evenwicht van dat zuur ook een rol speelt (de entropieterm gaat dan een grotere rol spelen).
|
08-01-2017