Bepalen van de gravitatieconstante 
mbv een slinger en een webcam

Datum: april 2006

Principe:

M.b.v. een slinger en een webcam en bijbehorende software voeren we de slingerproef uit waaruit we dan de waarde van g bepalen.

Materiaal:

  • Statief
  • Webcam
  • Draad 
  • Gewichten
  • Webcam software (in dit geval degene geleverd bij de Logitech WebCam die ik gebruikt heb).
  • Liniaal
  • Filmbewerkingssoftware (bv animation shop van paint shop pro)

Uitvoering:
  • Bouw de opstelling met slinger zoals op bovenstaande foto is aangegeven. 
  • Plaats de liniaal dusdanig dat de bal voor de liniaal zwaait.
  • Stel de webcam software in op 15 fps
  • Geef de bal een zetje zodat hij mooi parallel van de liniaal zwaait en neem een filmpje op.
  • Laad het filmpje in Animation Shop.
  • Tel het aantal frames van het begin van een zwaai totdat deze weer terug is.
  • Bereken hiermee de slingertijd en vervolgens de gravitatieconstante.

YouTube link: Slingerproef

Meetresultaten en uitwerking:
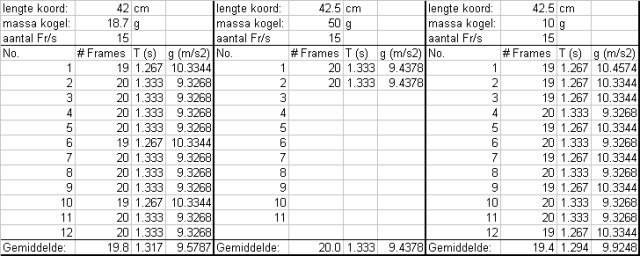
De resultaten zijn opgeslagen in de file slinger.xls.

Gemiddelde voor g: 9.65 m/s2

Discussie: 

We berekenen g met de formule die we hier beneden in achtergrondinformatie afgeleid hebben:

Volgens de tabellen is de waarde voor g die we moeten vinden: 9.81 m/s2.We vinden (niet helemaal eerlijk gemiddeld) een waarde van 9.65 m/s2.

Bekijken we de "gevoeligheden" in de gebruikte formule dan blijken er maar 2 echte variabelen in te zitten nl de trillingstijd en de koordlengte. Spelen we even met beide dan zien we de de grootste gevoeligheid in de trillingstijd zit. De resultaten laten ook zien dat we dan 19 frames en dan 20 frames meten hetgeen aangeeft dat de echte waarde daar waarschijnlijk tussenin zit. Indien we g berekenen uitgaande van 19.5 frames komen we inderdaad op een waarde van 9.81 m/s2 uit. Dit geeft aan dat onze methode om de slingertijd te bepalen niet nauwkeurig genoeg is. Om dit met een webcam nauwkeurig te kunnen doen zouden we het aantal fps moeten verdubbelen naar 30 fps.

In het hier uitgevoerde experiment hebben we de koordlengte niet veranderd, de massa aan het koord echter wel. We zien aan de resultaten dat de slingertijd onafhankelijk is van de massa die aan de slinger hangt. Dat klopt ook we als we als we naar de formule kijken, daarin staat nergens het symbool m. Kijken we naar de formule dan zien we dat de slingertijd wel afhankelijk is van de koordlengte.

 Conclusie:

  • Met de slingerproef kunnen we de waarde van g bepalen vooropgesteld dat we een methodologie hanteren die het mogelijk maakt om de slingertijd nauwkeurig te bepalen.
  • Bij een vaste koordlengte is de slingertijd onafhankelijk van de massa die we aan de slinger hangen.

Opmerkingen:

  • 15 fps is eigenlijk te weinig voor een goede meting. Beter is het om een webcam te gebruiken die 30 fps aankan.

Literatuur:

  • T.H. Savory; Natuurkunde Thuis; Thieme; 2de druk; p. 25-30.
  • Keith Caly; 'The Pendulum, Gravity, and that Number “9.8”' ; The Physics Teacher; Vol. 42, January 2004; p. 14,15.
  • Dr. J. Schweers en Drs. P. van Vianen; Natuurkunde op copusculaire grondslag - Deel drie voor de bovenbouw van het vhmo; Malmberg; 12de druk; 1964; p.1986, 1987. 
  • Raymond A. Serway and Jerry S. Faughn; College Physics; Thomson; 6th Ed; 2003; ISBN 0030351146; p. 402-406.
  • Niek de Kort; Klassieke Mechanica; Teleac; 1989; ISBN 9065332081; p.190-192.
  • Richard T. Weitner and Robert L. Sells; Elementary Classical Physics Volume 1; Allyn And Bacon; 2nd Ed.; 1973 (1965); ISBN 020503587; p. 270,271. 

Relevante websites:

Minder relevante websites

Achtergrondinformatie:

Als een punt periodiek dezelfde baan in de ruimte doorloopt zeggen we dat het punt een trilling (of oscillatie) uitvoert.
Een speciale trilling is voor ons van groot belang “de harmonische trilling”.
De eigenschappen zijn dat het een beweging is langs een rechte lijn die wordt beschreven door:

                              

  • Het tijdsinterval waarin een volledige beweging plaats heeft noemt men de periode of trillingstijd T (in s).

  • De frequentie f (of n) is het aantal trillingen per tijdseenheid waarbij f = 1/T (in Hz of 1/s).
  • Met de cirkelfrequentie w bedoelen we de hoeksnelheid van een punt:
                                                                          w=2.    p.f = 2.p/T  (= hoek/tijd).
  • Onder de uitwijking u verstaan we de afstand die het harmonisch bewegend punt heeft afgelegd sinds de laatste doorgang door de evenwichtsstand.
  • De amplitudo A is de maximale uitwijking.

De harmonische beweging kan afgeleidt worden uit een eenparige cirkelbeweging.

Stel, dat punt p eenparig de cirkel doorloopt. De projectie van P op de verticale middellijn is Q.

 als 2p = T (s) en  j = t (s) dan

De fase van een trillend punt is het quotiënt van de tijd, verlopen sinds een bepaalde doorgang door de evenwichtstoestand en de trillingstijd: j = t/T

De snelheid van een harmonische trillingen kunnen we afleiden uit de differentiaalvergelijking:

De versnelling van een harmonisch trillend punt kunnen we ook weer mbv een differentiaalvergelijking afleiden:

Omdat de versnelling steeds het gevolg is van een kracht die op een massa werkt en die massa daardoor een versnelling heeft geldt:  

c noemen we de veerconstante.

Hieruit volgt dat:

Dit is de trillingstijd van een veersysteem.

Een ander voorbeeld is de mathematische slinger.

Als we een massa vanuit de evenwichtsstand naar punt p brengen en hem daar loslaten, dan wordt de massa door een component van de zwaartekracht G naar de evenwichtsstand terug gedreven.

Nu geldt:



Voor kleine hoeken geldt sina/a=1 
dus:
 

Voor de slingertijd geldt:

De slingertijd is de tijdsduur die verloopt tussen twee momenten waarop een punt (bijvoorbeeld de massa) van een slinger zich weer op hetzelfde uiteinde bevindt. 

De slingertijd wordt ook wel periode genoemd.

Uit de formule van de slingertijd kunnen we afleiden dat de periode van een slinger alleen maar afhankelijk is van de lengte van de slinger en de gravitatieconstante. Ook speelt de amplitudo niet een bijzonder grote rol zolang deze relatief klein is (sinusbenadering moet blijven gelden). Deze afhankelijkheid maakt het mogelijk de slinger als klok te gebruiken. 

Galileo was de eerste die opmerkte dat de periode van een slinger onafhankelijk is van zijn amplitudo. 

Geologen maken gebruik van een slinger als ze op zoek zijn naar olie en mineralen. Afzetting beneden het oppervlak van de aarde kunnen afwijkingen in de gravitatieconstante veroorzaken. Door gebruik te maken van een speciaal ontworpen slinger van bekende lengte wordt de periode gemeten, die dan weer gebruikt wordt om g te berekenen. 

17-01-2017