Zelfgebouwde spectroscoop

Datum:

juni 2004

Principe:

Met een spectroscoop kunnen we het spectrum van een lichtbron bestuderen.

 Materiaal:

  • Kartonnen doos
  • CD
  • Zwarte pen
  • Snijmes
  • Zwart papier
  • Scheermesjes

Uitvoering:

De spectroscoop is opgebouwd uit 3 delen. Een spleet gemaakt met scheermesjes, een rooster gemaakt van een CD en een kijkbuis gemaakt van een WC rolletje.

Om er zeker van te zijn dat alle onderdelen goed opgelijnd zijn maken we gebruik van de CD als meetinstrument en markeren de plaats waar de spleet en de kijkbuis geplaatst moeten worden.
Zet de CD disk boven op de doos, ca. 1-1.5 cm van de linkerkant en dicht bij de bodem, zoals weergegeven op bovenstaande foto. Gebruik een pen  om een cirkel te tekenen van de binnenkant van de CD. Dit geeft de plaats aan waar we het WC-rolletje gaan monteren.

Plaats nu het WC rolletje op de doos, waarbij de cirkel die we zojuist getekend hebben gecentreerd is. Teken een tweede cirkel langs de buitenkant van de WC rol.

Verschuif het rolletje een beetje (ca. 1-1.5 cm). Teken een tweede cirkel op dezelfde manier. Deze cirkels geven aan waar er gesneden moet worden. 

Snij nu een ovaal uit de doos met een scherp mes. Deze ovaal maakt het mogelijk om de kijkbuis onder een hoek te in de doos te laten gaan.

De tweede stap is het maken van een spleet. Draai de doos een kwartslag om, zodat de zojuist uitgesneden ovaal rechts komt. Teken mbv de CD weer een kleine cirkel dicht bij de linkerkant van de doos.

De spleet zit nu aan de linkerkant van de doos. Snij een kleine rechthoek uit de door ter hoogte van de cirkelmarkering. Deze moet ca. 1-1.5 cm breed en ca. 5 cm hoog zijn. 
Haal voorzichtig (!!!) twee scheermesjes tevoorschijn en plaats ze boven de rechthoek. Plak ze dan vast met tape maar let erop dat de mesjes elkaar net niet raken. Zorg ervoor dat de mesjes evenwijdig lopen.

Plaats de doos met de rechterkant omhoog, met de spleet naar je toe. Tape nu de CD met dubbelzijdig plakband vast aan de achterste kant van de doos. De regenboog kant moet naar je toe wijzen. De linkerkant van de CD moet evenver van de linkerkant van de doos geplaatst worden als de spleet is.  
Tape nu alle plaatsen dicht met tape waar licht in de doos kan vallen. Gebruik hiervoor aluminium tape of aluminium folie.

Gebruik de tape om de kijkbuis vast te zetten. Let erop dat je een goede afdichting maakt die lichtdicht is. Probeer de hoek goed vast te zetten door eerst door de buis te kijken. Houdt de spleet richting een lichtbron en kijk door de buis. Verander de hoek dusdanig totdat je een spectrum kunt waarnemen.

Meetresultaten en uitwerking:

Houdt de spleet richting een lichtbron.

Een heldere lichtbron zal een eenvoudig spectrum laten zien zonder scherpe lijnen. De reden is dat het licht van een hete vaste stof komt (het wolfraam filament in de gloeilamp)

Hete gassen produceren licht dat maar uit een paar kleuren is opgebouwd. Een spectroscoop zal deze kleuren uit elkaar halen waardoor ze apart zichtbaar worden.

Discussie: 
De putjes op een  CD hebben een variabele lengte van 0.9-3.3 µm lang, 0.6 µm breed en 0.12 µm diep. De lengte van de putjes wordt als een code uitgelezen bij het draaien van de CD, daarom moet de lengte tot op 0.05 µm nauwkeurig bepaald zijn. De naast elkaar gelegen tracks functioneren als lijnen in het diffractierooster, waarbij de tracks (en dus de roosterlijnen) ca. 1.6 µm van elkaar liggen. Verschillende golflengtes (kleuren) licht worden onder een andere hoek weerspiegeld aangezien de diffractiehoek afhankelijk is van de golflengte.
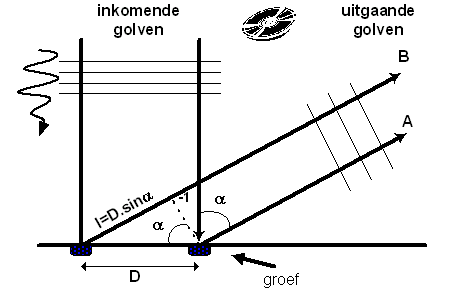Bekijken we een klein deel van de CD waar licht loodrecht opvalt. Als alle groeven tegelijkertijd belicht worden door het invallende lucht zal elke groef een lichtgolf uitzenden in alle richtingen. De uitgaande golf is het resultaat van een superpositie van al deze individuele golven. Het licht van de linkergroef in de schets hierboven loopt iets achter op de golf die uit de rechter groef komt aangezien de weglengte langer is met l = D sin(al). 
Als het weglengteverschil gelijk is een aan een halve golflengte (of een oneven veelvoud daarvan) dan valt de piek van golf A samen met het dal van golf B en doven de golven elkaar uit. Als l echter overeenkomt met een volledige  golflengte (of een veelvoud daarvan), zal er een overlap plaatsvinden met de piek van de golf van de daarnaastgelegen groef en vindt er dus versterking plaats in die richting. Aangezien de afstand tussen de groeven overal op de disk hetzelfde is, zullen alle groeven aan het resultaat bijdragen. Dit betekent dat we alleen een sterke reflectie krijgen in de richting sin(al) = l/D (of een veelvoud van l/D). Aangezien deze richting afhankelijk is van de golflengte is het mogelijk een spectroscoop te bouwen met een diffractie rooster. Voor de CD weten we dat D = 1.6 micro-meter, en kunnnen we de deflectiehoek (al) berekenen voor elke kleur van het (1ste orde) spectrum:

 
kleur golflengte (nm) deflectiehoek (o)
rood 650 24
oranje 600 22
geel 575 21
groen 550 20
blauwgroen 500 18.5
blauw 450 16.3
paars 400 14.5

Een nauwkeurige meting van de hoek maakt het dus mogelijk om de golflengte te bepalen. Aan bovenstaande tabel kunnen we zien dat de hoek nagenoeg lineair oploopt met de golflengte. We kunnen dus de golflengte van een kleurlijn afschatten door de afstand tot een bekende kleur te bepalen, zoals de Na D lijn op 590 nm of de Hg lijnen op 579 en 577 nm (geel), 546 (groen), 436 (blauw) en 405 (paars).

De regenbogen die we in het experiment maken zijn 1ste reflecties (1 golflengte weglengte verschil tussen naastgelegen stralen), in het centrum is het 0de orde beeld en de zwakkerre bogen verder weg de 2de orde spectra.

De CD heeft ook enkele beperkingen als hij voor dit doel gebruikt wordt. De CD is nl ontworpen om te werken met het IR-licht in de CD speler en de afstand tussen de groeven is een belangrijke factor voor de scheiding. Daarom werkt de CD niet zo goed bij kortere golflengte in het blauwe en paarse gebied. De zeer sterke lijnen van geïoniseerd calcium (de H en K lijnen) op 393 en 397 nm kunnen niet gezien worden met een CD spectroscoop.

Men kan betere diffractie roosters maken met rechte lijn groeven en een betere optische kwaliteit verkrijgen door glas of metaal als basis te gebruiken. De uitvinder van het rooster Henry A.Rowland  (1880) produceerde al roosters op exact gebogen oppervlakte waardoor het mogelijk werd de spectra te focusseren.

Conclusie:
  • Een CD kan als reflecterend tralierooster gebruikt worden.

Opmerkingen:

  • Oppassen met die scheermesjes, je snijdt je er heel makkelijk mee in de vingers. Ondergetekende kan er over meepraten.
  • Met een CD zonder aluminium laag zou je in principe lichtbreking zonder reflectie kunnen bereiken.
    •

Literatuur:

  • Johannes van Zeeland, Thomas van Dijk; 'Dubbele Spectroscoop'; DJO; 3 1974; p.72-74.
  • R.J. Flink; "Fysische Optica"; Nijgh & Van Ditmar; 1ste druk; 1992; ISBN 9023606728, p.55-59.
  • Ulrich Dammgen and Herbert Keune; 'A Simple Device for Obtaining Visible Spectra'; Journal of Chemical Education; 2 62 1985; p. 155,156.

Relevante websites:

Achtergrondinformatie:

Spectra 

Zeer veel spleten naast elkaar vormen een tralie of rooster. Als je monochromatisch licht op een tralie laat vallen dan ontstaat een stelsel van lijnen, het zgn interferentiepatroon. Een tralie kan worden gemaakt door zwarte lijnen op een witte achtergrond fotografisch sterk te verkleinen. Hoe dichter de spleten bij elkaar zitten, hoe wijder het patroon zal worden en hoe nauwkeuriger de golflengtes bepaald kunnen worden. Een CD is een reflectietralie. De kleuren worden veroorzaakt door sporen die op 1.6 micrometer van elkaar zitten.  

enkele spectra 

wit licht

stikstof

waterstof

natrium
Roostertheorie

Een buigingsrooster bestaat uit een vlakke glazen plaat met hierop een dunne laag aluminium gedampt. Hierin zijn een groot aantal evenwijdige krassen op onderling gelijke afstand aangebracht. Hierdoor wordt een buigingsbeeld verkregen.

De roosterconstante d is de afstand tussen twee opeenvolgende krassen. In het buigingsbeeld zien we bij monochromatisch licht een aantal heldere gekleurde lijnen waartussen het donker is. Bij wit licht nemen we aan weerszijden van de heldere witte lijn, het centrale maximum, een aantal volledige spectra waar. Om dit buigingsbeeld te verklaren gebruiken we de opstelling zoals die oorspronkelijk door Fraunhofer gebruikt werd waarbij de belichting van het rooster plaatsvindt door een evenwijdige monochromatische lichtbundel en een lens (L) achter het rooster (T) geplaatst is. Deze lens zorgt voor de afbeelding van het interferentiebeeld in het brandvlak van de lens zoals hierbeneden is weergegeven. 

We kunnen de theorie van Huygens gebruiken om het verband af te leiden dat bestaat tussen de ligging van de ontstane heldere lijnen en de gebruikte golflengte (l). Aangezien er een evenwijdige lichtbundel loodrecht op het rooster valt zijn alle punten (1...6) onderling in dezelfde fase en zijn nieuwe trillingscentra die in alle richtingen golven uitzenden. De golven die rechtdoor gaan komen in fase in het hoofdbrandpunt P samenkomen. In dit punt zal vanwege de optredende versterking maximale lichtintensiteit heersen (centrale maximum). Golven die onder een hoek a worden uitgezonden lopen tot de lijn CD allemaal verschillende optische wegen (de weglengte is verschillend) zodat ze op deze lijn allen een verschillende fase hebben. Vanaf CD tot P' wordt wel dezelfde weg afgelegd, hetgeen betekent dat het onderlinge faseverschil gehandhaafd blijft.

In P' zal weer maximale intensiteit optreden als het weglengteverschil tussen twee opeenvolgende spleten tot aan de lijn CD een verschil heeft van 1 golflengte (de punten op de lijn hebben dan dezelfde fase). Uit bovenstaande figuur kun je dan afleiden:

 De volgende maxima, gerekend vanaf het centrale maximum moet voldoen aan:

Als n=0 spreken we van het 0de orde maximum, als n=1 van een 1ste orde maximum, etc. De lichtintensiteit neemt af naarmate n toeneemt.

 

12-01-2017