Kubus van weerstanden

Datum: Januari 2016

Principe: Vervangingsweerstand meten en berekenen.

Materiaal:

 
  • 12 weerstanden (hier 470 Ohm)
  • Soldeerbout en soldeertin
  • Multimeter met weerstandsmeting
     

Uitvoering:

  • Soldeer de kubus in elkaar volgens nevenstaand schema.

  • Verbind de multimeter met twee hoekpunten zoals weergegeven in onderstaande schetsen en voer een weerstandsmeting uit,

  • Bereken de vervangingsweerstandswaarde voor de verschillende configuraties en controleer of deze overeenkomt met de gemeten waarde.

Uitvoering en resultaten:

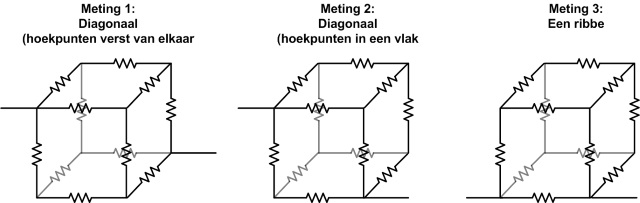
De gesoldeerde kubus met op elke ribbe een weerstand van 470 Ohm.
Meting 1
Meetwaarde: 391 Ohm
Meting 2
Meetwaarde: 352 Ohm
Meting 3
Meetwaarde: 275 Ohm
 
Berekeningen
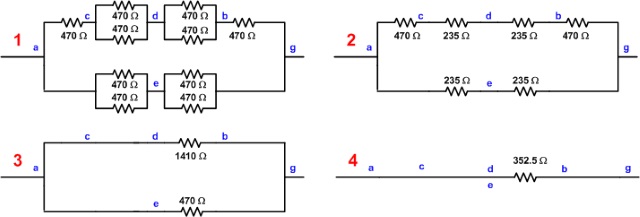
  Meting 1
Aangezien de kubus symmetrisch is betekent dit dat de stroom (I) evenredig gesplitst wordt met I/3 over elke tak. Bij de daaropvolgende splitsing (bv c) wordt de stroom verder verdeeld met I/6  gaande door pad ce en cd. De sroom die door de weerstand in db gaat is de som van de stromen fd en cd: I/6+I/6 = I/3.

Het potentiaalverschil tussen A en B kan dan geschreven worden als:

Vab = Vac + Vcd + Vdb = I/3.R+I/6.R+I/3.R = 5/6.I.R

Hetgeen een  vervangingsweerstand geeft van:

Rv = 5/6.R = 5/6.470 = 392 Ohm.
 

Men kan het geheel ook uittekenen zoals in onderstaand schema gebeurd is en vervolgens met de vervangingsweerstandsformules de overall vervangingsweerstand berekenen.

  Meting 2
De oplossing van dit schema wordt bepaald door het gegeven dat de hoekpunten d en e in de kubus identiek zijn m.b.t. de stroomverdeling voor verschillende paden. Men kan dan onderstaande schema's opstellen om op een oplossing uit te komen.

Voor de vervangingsweerstand geldt:

Rv = 3/4.R = 3/.470 = 352.5 Ohm.
 

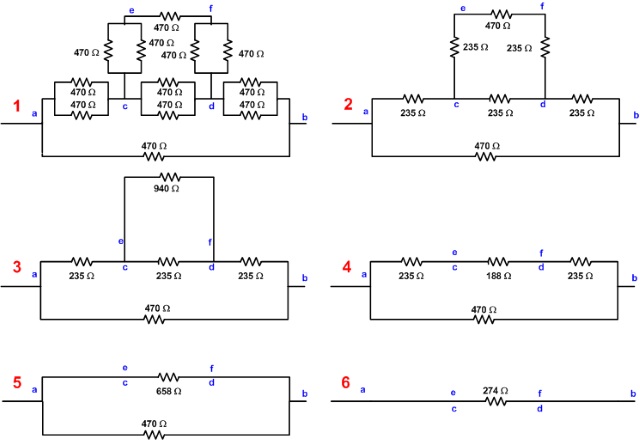
  Meting 3

Ook hier geldt dat de oplossing van dit schema wordt bepaald door het gegeven dat  hoekpunten c en d in de kubus identiek zijn m.b.t. de stroomverdeling voor verschillende paden. Men kan dan onderstaande schema's opstellen om op een oplossing uit te komen.

Voor de vervangingsweerstand geldt:

Rv = 7/12.R = 7/12.470 = 274 Ohm. 

Discussie en conclusie:

In onderstaande tabel zijn de gemeten en de berekende waardes samengevat

We zien een zeer goede overeenkomst tussen de gemeten en de berekende waardes. Het verschil van 1 Ohm (< 1% relatief) valt binnen de foutenmarge die voor dit type koolweerstanden wordt opgegeven (1%).

Literatuur:

  • Dirksen; "Leerboek Elektronica - Deel 1"; De Muiderkring; 9de druk; 1979; ISBN 906082101'; p. 42-58.
  • R.J. Flink; "Elektriciteitsleer"; Nijgh & Van Dirmar; 1992; ISBN 9023606736; p. 13-15.

Relevante websites:

Opmerkingen:

  • In dit geval hen ik een weerstand van 470 Ohm gebruikt. Men kan dit experiment natuurlijk met elke weerstandswaarde uitvoeren die men tot zijn beschikking heeft.

Achtergrondinformatie:

Door meerdere weerstanden te vervangen door één weerstand wordt een schakelingen vaak een stuk eenvoudiger en kunnen stroom en spanning makkelijker uitgerekend worden. Zo'n weerstand wordt een vervangingsweerstand genoemd (Rv). Het verschil tussen een serie- en parallelschakeling is dat bij de serieschakeling door alle weerstanden dezelfde stroom gaat en bij een parallelschakeling door elke weerstand een deel van de stroom gaat,

De regels voor het berekenen van een vervangingsweerstand voor serie- en parallelschakelingen zijn dan:

Serieschakeling: Rv = R1 + R2+… (Ω)

Parallelschakeling: 1/Rv = 1/R1+1/R2+…  (1/Ω)

 

08/01/2016