Arduino gebruiken om een harmonische beweging te bestuderen


|
Arduino gebruiken om een harmonische beweging te bestuderen |

|

|
Datum: Mei 2017
Inleiding:
| De Arduino is een prachtig platform om wetenschappelijke experimenten mee uit te voeren. |
Principe:
| Ultrasone afstandssensor gebruiken om een veer te karakteriseren. |
Materiaal:
|
|
|
|
Uitvoering:
 |
|
| Methode 1: Arduino | Methode 2: Klassiek |
|
|
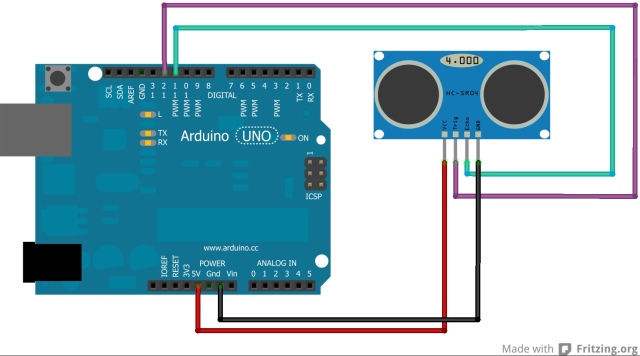 |
|
| Sketch code | |
|
/* * Define the pins you want to use as trigger and echo. */ #define ECHOPIN 11 // Pin to receive echo pulse #define TRIGPIN 12 // Pin to send trigger pulse /* * setup function * Initialize the serial line (D0 & D1) at 115200. * Then set the pin defined to receive echo in INPUT * and the pin to trigger to OUTPUT. */ void setup() { Serial.begin(115200); pinMode(ECHOPIN, INPUT); pinMode(TRIGPIN, OUTPUT); } /* * loop function. * */ void loop() { // Start Ranging digitalWrite(TRIGPIN, LOW); delayMicroseconds(2); digitalWrite(TRIGPIN, HIGH); delayMicroseconds(10); digitalWrite(TRIGPIN, LOW); // Compute distance float distance = pulseIn(ECHOPIN, HIGH); distance= distance/58; Serial.println(distance); delay(200); } |
|
Er steken 4 pinnen uit de module : VCC ,
Trig, Echo, GND . Dat maakt het een gemakkelijk interface voor de
microcontroller. Het programma voert de volgende bewerkingen uit:
|
|
Resultaten:
| Veerconstante bepalen met de klassieke methode | |||||||||||||||||||||||||||||||||||||
|
De meetresultaten zijn weergegeven in
nevenstaande tabel en onderstaande grafiek. Deze laat in eerste instantie een mooie correlatie zien tussen uitrekking en gewicht, hetgeen suggereert dat we het experiment goed uitgevoerd hebben. Met deze grafiek kunnen we echter niet de veerconstante uitrekenen. Daarvoor moeten we de meetresultaten converteren. |
||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Op het oog lijken de resultaten in de eerste grafiek goed te voldoen (correlatie & rechte lijn). De E-u grafiek ziet er echter iets minder mooi uit. | ||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| De Arduinomethode | |||||||||||||||||||||||||||||||||||||
|
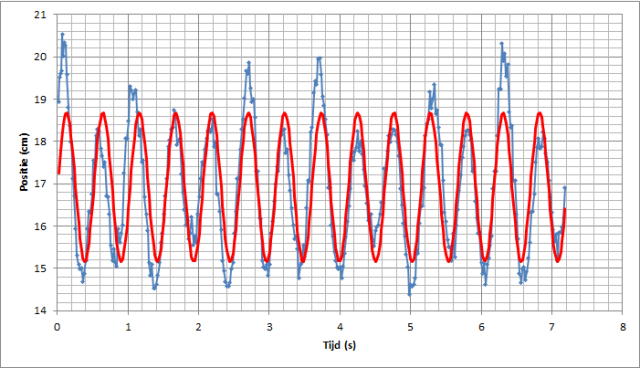
Als men in de leerboeken een dergelijke
methode toepast dan lijkt het resultaat altijd uit mooie sinusgolven te
bestaan. De werkelijkheid is anders zoals men in onderstaande grafiek kan
zien. De blauwe lijn geeft de oorspronkelijke meetresultaten aan. Daar is
moeilijk informatie uit te halen daarom besloot ik een trucje toe te passen.
De sinusgolf van een veer wordt beschreven door de formule u = A.sin(2.pi.f.t)
waarin f staat voor de frequency factor en A de Amplitude. Door nu de verschillende componenten individueel te bepalen m.b.v. een eenvoudige chi^2 toets, zoals geschetst in onderstaande tabel, kan men de belangrijkste kengetallen (A,f) bepalen en zo een sinusgolf simuleren. Het resultaat kan men zien in onderstaande grafiek, de rode lijn matcht redelijk (weliswaar duidelijke uitschieters) met de meetdata. |
|||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
|
Op deze manier berekenen we een veerconstante van 5.3 N/m hetgeen redelijk overeenkomt met de waarde die we gevonden hebben via de klassieke methode. |
|||||||||||||||||||||||||||||||||||||
Discussie:
| Dit experiment is een beetje slordig uitgevoerd omdat het eigenlijk doel was om met de Arduino en Echo locatie te spelen. Voor een meer zuiver wetenschappelijk experiment had ik ook met meerdere veren aan de slag moeten gaan. Ook had ik de data-analyse kunnen opvoeren en bv dempingfactoren gaan bepalen. Desalniettemin laat het experiment duidelijk zien dat beide methoden vergelijkbare resultaten opleveren. |
Conclusie:
|
Opmerkingen:
|
Literatuur:
|
Relevante websites:
Minder relevante websites:
|
Achtergrondinformatie: Arduino Arduino is een opensource-computerplatform (printplaat, computer) bedoeld voor iedereen die geďnteresseerd is in het maken en ontwerpen van objecten die kunnen reageren op hun omgeving, door het aansluiten van allerlei sensoren en actuatoren op de Arduino. Via de sensoren kan digitale en analoge inputsignalen genereren die door de Arduino verwerkt worden en dan weer een actie kunnen initiëren door het afgeven van digitale en analoge outputsignalen. Input kan bijvoorbeeld worden gegenereerd door schakelaars, lichtsensoren, bewegingsmeters, afstandsmeters, temperatuursensoren, of op basis van commando's afkomstig van internet, een radiomodule of een ander apparaat met een seriële interface. Outputsignalen kunnen bijvoorbeeld motoren, lampjes, pompjes en beeldschermen aansturen, maar ook input genereren voor een andere Arduinomodule. Op de Arduino kan men zogenaamde "shields" zetten door dezen op de input-/outputpinnen van de Arduino te plaatsen. Deze shields kunnen bv extra functie toevoegen of verschillende sensoren en modules in één printplaat combineren. Het meest bekende shield is het ProtoShield dat dienst doet als breadboard, om op te experimenteren. |
|
Harmonische trilling |
|
Eén van de basis regels die het universeel geldig zijn is dat elk fysisch systeem, dat energie kan uitwisselen met zijn omgeving, streeft naar een toestand van minimale energie. Een toestand van minimale energie noemt men ook wel de rusttoestand, stabiele evenwichtspositie of minimale energietoestand. Elk systeem dat uit evenwicht gebracht is zal er naar streven om weer een minimale energietoestand te bereiken. Als de kracht die het systeem naar de evenwichtstoestand brengt evenredig is met de uitwijking t.o.v. de evenwichtstoestand voert het systeem een enkelvoudige harmonische beweging uit. Bij zulk een trillend systeem spreekt men ook wel van een enkelvoudige harmonische oscillator. Als men het systeem beperkt tot de de verticale beweging van een massa m aan een veer in het zwaarteveld dan wordt de terugroepende kracht F gegeven door de wet van Hooke: F = -kx waarin x de uitwijking is van de massa ten opzichte van de evenwichtstoestand (x = 0). De constante k noemt men de krachtconstante van de veer of de veerconstante. Het minteken in deze uitdrukking duidt erop dat de nettokracht in de tegenovergestelde richting wijst dan de verplaatsing x. Wanneer een massa aan de veer gehangen wordt, streeft het systeem opnieuw naar evenwicht. Dit evenwicht wordt bereikt als ∑F = 0. Op de massa werkt enerzijds de zwaartekracht, anderzijds de kracht uitgeoefend door de veer (zie onderstaande figuur). Er wordt evenwicht bereikt als: ∑F = mg – kx0 = 0
Fig.: (a) Vrij bewegende veer, verticaal opgehangen. (b) Massa m bevestigd aan de veer in nieuwe evenwichtspositie, die bereikt wordt als ∑F = 0 = mg – kx0. Als de veer uit evenwicht gebracht wordt door een kleine uitwijking u te geven aan de veer, zal er een extra kracht werken op de massa met als bedoeling de veer opnieuw in evenwicht te brengen. Als er nu een resulterende kracht optreedt zal de massa een versnelling ondergaan: ∑F = mg – k(x0 + u) = - ku = ma of
De oplossing van deze differentiaalvergelijking geeft aanleiding tot harmonische trillingen. Vermits de wrijving van de bewegende massa verwaarloosd werd, zal de trilling onveranderd blijven. Men spreekt van een vrije, ongedempte trilling. De massa m beweegt dan op en neer met een bepaalde frequentie die niet afhangt van de amplitude van de trilling. We noemen deze frequentie de natuurlijke trillingsfrequentie van de massa aan de veer. Deze frequentie wordt gegeven door:
|
24/06/2017