De Wet van Snellius

Datum:  December 2018

Inleiding:

Bij AliExpress heb ik ooit voor weinig geld een optica experimenteerdoos gekocht die zich goed leent voor het uitvoeren van dergelijke experimenten.

Materiaal:

  • Opticadoos met perspex halve schijf en lijnlaser
  • Goniometer (gradenboog van 360 °)
  • PC met Excel

Uitvoering:

  • Het experiment wordt uitgevoerd met een enkele straal van de lijnlaser.
  • Plaats de perspex halve schijf op de goniometer zoals aangegeven op onderstaande foto's.
  • Positioneer wat preciezer m.b.v. een lichtstraal die loodrecht op het midden van de schijf valt.
  • Bepaal vervolgens bij verschillende invalshoeken (i) de brekingshoeken (r).
  • Noteer zowel de invallende hoek als als de brekingshoek.
  • Let erop dat de invallende straal exact  op het midden van de vlakke zijde valt.
  • Voer dit experiment uit voor lucht-perspex en voor perspex-lucht.
  • Evalueer de metingen m.b.v. Excel.
    Bepaal de hellingshoek, forceer daarbij de oorsprong door 0.
Grensvlak: lucht - glas Grensvlak: glas - lucht

Schets

Resultaten:

De meetresultaten zijn samengevat in onderstaande tabellen en grafieken.

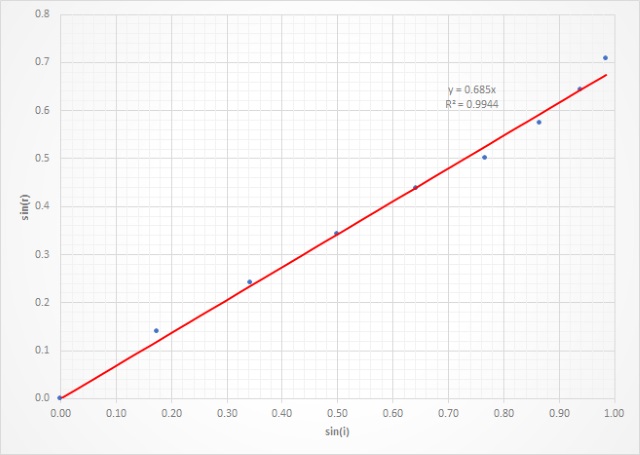
Breking lucht naar perspex

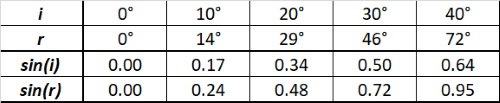
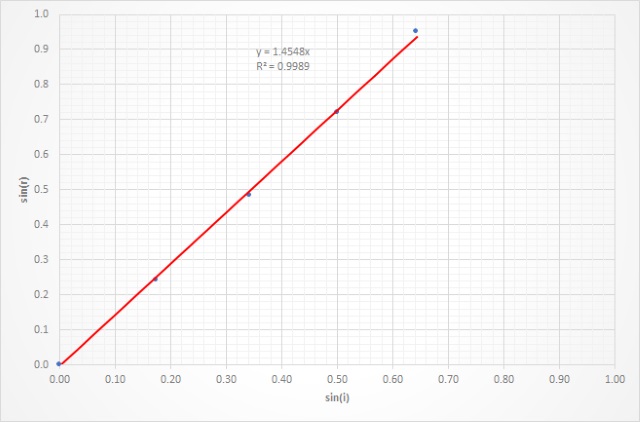
Breking perspex naar lucht

Discussie en conclusie:

Het was de Nederlander Willbrord Snel, van Royen (1851-1626), die voor het eerst ontdekte dat bij overgang van licht van de ene stof naar de ander het quotiënt van de sinussen van de hoek van inval en de hoek van breking  een bepaal getal is. In zijn tijd publiceerde men in het Latijn en hij ondertekende dan ook met zijn Latijnse naam "Snellius", vandaar dat me spreekt van de "Wet van Snellius". De grootte van de verhouding sin(i)/sin(r) wordt de brekingsindex genoemd. De brekingsindex (n) hangt af van de aard van de stoffen aan weerszijden van het scheidingsvlak.

In formule:

M.b.v. de formule kan men zien dat voor n>1 de brekingshoek kleiner is dan de hoek van inval. De breking is naar de normaal (de loodlijn op het grensvlak) gericht. De gebroken straal licht in het vlak van de invallende straal en de normaal op het grensvlak. De stof waar het licht dan intreedt nomen men een optisch dichtere stof. Bij n<1 is de breking van de normaal af en spreekt men van een optisch minder dichte stof.

Uit de meetresultaten bepalen we de volgende hellingshoeken:

  • lucht naar perspex: 0.685
    met n = sin(i)/sin(r) --> n = 1/0.685 = 1.46
  • perspex naar lucht: n = 1.45

Binas geeft ons de volgende brekingsindexen voor perspex:

rood - 687nm: 1.49
geel - 589 nm: 1.49
blauw - 486 nm: 1.50
violet - 434 nm: 1.50
Grenshoek bij 589 nm (geel): 42.2 °

De grenshoek van 42.2° conformeert dat we bij het perspex- lucht systeem geen meting met een hoek boven de 40° konden uitvoeren.

We maken gebruik van een rode laser maar onze meetresultaten wijken af van de door Binas opgegeven waarde van 1.49. Aan deze afwijking kunnen verschillend factoren een bijdrage geleverd hebben:

  • De lichtstraal die door de opening komt is relatief breed hetgeen nadelig is voor de afleesnauwkeurigheid.
  • We weten niet zeker of het materiaal van de schijf wel zuiver perspex is en niet ook een ander materiaal bevat hetgeen een materiaal met een iets afwijkende brekingsindex kan opleveren.
  • We hebben dit experiment maar een keer uitgevoerd. Meerdere malen uitvoeren levert een statistisch gezien betrouwbaarder resultaat op.
    Bij het richten en meten kunnen we kleine fouten maken die we op deze manier kunnen uitmiddelen.

Bij de meting van lucht naar perspex vindt er geen hoekafwijking plaats als de lichtstraal uit de ronde zijde van de schijf komt. De verklaring is dat de brekingsindex van lucht 1.00 is, hetgeen betekent dat de hoek van  inval en de hoek van breking gelijk zijn.

Opmerkingen:

  • In oudere boeken wordt de brekingsindex ook wel "brekingsaanwijzer" genoemd.

Literatuur:

  • Ir.J.T.van Konijnenburg; "Natuurkunde Zien end Doen"; Agon Elsevier (Heron); 1973; ISBN 9010104354; blz. 229-235.
  • J.C. Alders; "Ons acoustisch en Optisch Laboratorium"; Enum- Amsterdam; 1948; p. 108-128.
  • Binas: Noordhoff; 2008; 5de druk; ISBN 978-9001893805; p. 18A

Relevante websites:

Minder relevante websites:

Achtergrondinformatie:
We hebben de wet van Snellius op een vereenvoudigde manier besproken. Een iets meer gedetailleerde omschrijving is:

De brekingsindex van een stof is gedefinieerd als de verhouding van de lichtsnelheden in vacuüm (of lucht) en in de betreffende stof. Bij een bepaalde temperatuur en golflengte is het een stofconstante. De brekingsindex van een vloeistof kan ons iets zeggen over zijn zuiverheid, zijn aard, zijn concentratie in een oplosmiddel of de mengverhouding met een andere stof. Een monochromatische lichtstraal, gaande van een minder dicht medium naar een dichter medium, wordt in het algemeen gebroken naar de normaal toe.

Volgens de Wet van Snellius geldt daarbij:

waarbij n1 de brekingsindex is van de stof met een lagere dichtheid en n2 de brekingsindex van een stof met een hogere dichtheid.

27/12/2018