Calorimeter met CoachLab

Experimenteren met een Calorimeter (Coachlab)

Datum: Maart-Mei 2020

Inleiding:

Ik heb deze calorimeter al een tijdje geleden bij AliExpress gekocht en het werd tijd om er mee te experimenteren.

Principe:

De dubbelwandige calorimeter kan gebruikt worden om de specifieke warmte van vast stoffen te bepalen. Door gebruik te maken van het ingebouwde verwarmingselement kan men het elektrische equivalent bepalen.

Materiaal:

Calorimeter (22201) Roerboon Temperatuursensoren (CMA 0511) Coachlab II+ Kabels met bananenstekkers Balans Bekerglas Horlogeglas Aluminium blok Kaliumchloride (KCl) Water Computer met Coachlab software en Excel geïnstalleerd. Velleman PS1503SB voedingsbron Multimeters (Velleman DVM9912 en Voltcraft VC820)	Coachlab II+ Temperatuur sensor
Calorimeter: De binnenbeker heeft een volume van 150 ml en is naar buiten toe geïsoleerd m.b.v. schuimplastic en een plastic afdichtring. Het transparante deksel bevat openingen voor het verwarmingselement, de roerder en een kurk waar een thermometer doorheen past. De verwarmingsspiraal opereert m.b.v. een 0 - 6 V, 1.7 - 2A gelijkspanningsbron. 100 ml water wordt in 10 min met 10 °C verwarmd. De weerstand van de verwarmingsspiraal is ca. 2 - 3 Ohm.

Uitvoering:

Bouw de opstelling op zoals weergegeven in onderstaand schema.


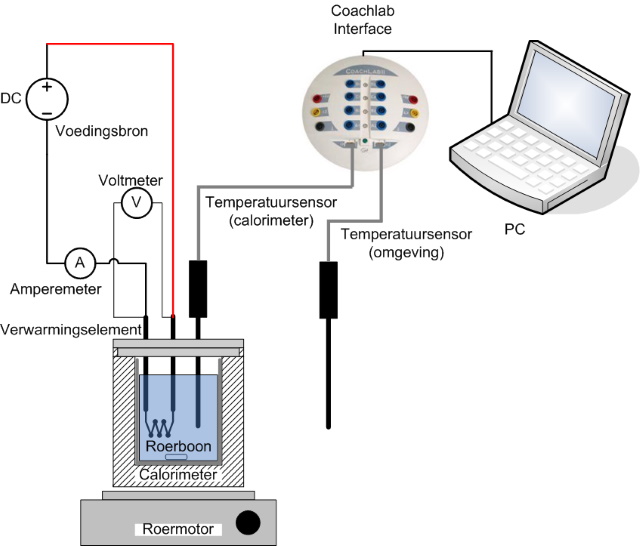Bepalen van de weerstand van de weerstandsdraad
Zet een van de multimeters op weerstandsmeting en gebruik deze om de weerstand van de draad te meten.
Bepalen van de soortelijke warmte van water
Haal de aluminium beker uit de calorimeter Weeg de beker Plaats de roerboon in de beker en weeg opnieuw Weeg ca. 100-150 g water af in de aluminium beker en plaats vervolgens de beker terug in de calorimeter Zet de deksel erop en controleer of alles goed is aangesloten. Let er vooral op dat de weerstand onder de waterspiegel zit. Zet de roermotor aan Stel de voedingsbron op en stel deze zo snel als mogelijk is in op het leveren van een constante stroomsterkte van ca. 1.7 - 1.8 A. Zet vervolgens de voedingsbron uit. Start de PC en de CoachLab software op en laad in Coachlab de activiteit "calorimeter" Zet de roermotor aan en roer rustig Wacht tot beide temperatuursensors ongeveer dezelfde temperatuur aangeven Zet de multimeters aan Zet de voedingsbron aan en start tegelijkertijd de Coachlab activiteit Noteer het voltage en het Amperage dat op de multimeters weergegeven wordt (t=0) In de activiteit zelf loopt een timer mee zoals op onderstaande screenshot te zien is Elke minuut wordt een temperatuur meting gedaan. Noteer dan ook Voltage en Amperage De activiteit duurt ca. 20 minuten waarin gedurende 10 minuten opgewarmd wordt Analyseer de verzamelde data.

In mijn geval heb ik dat gedaan door de data te exporteren en in te lezen in Excel Tabelleer de verzamelde data en zet deze ook grafisch uit zoals weergegeven in onderstaande voorbeelden


Bepaal van beide datasets de regressie lijn en noteer de hellingshoek Bereken het elektrisch geleverd vermogen m.b.v. P = U * I gedurende de opwarmtijd.
Experimentele bepaling van de soortelijke warmte van aluminium
Plaats de calorimeter op een balans en vul deze met ca. 125 ml water dat op kamertemperatuur gebracht is. Noteer de hoeveelheid water die in bewerking genomen is Voeg een roerboon toe Plaats de calorimeter op de roermotor en zet deze aan Bepaal m.b.v. een elektronisch balans de massa van het aluminium blok. Bevestig een dunne draad aan het Al blok Plaats een aluminium blok in een bekerglas met kokend water. Start Coachlab en laat het gedurende ca. 1 min draaien om de temperatuur van het water te bepalen Haal het blok uit het kolkend water en plaats het zo snel als mogelijk is in de calorimeter. Zorg ervoor dat de roerboon kan blijven draaien door het blok met de draad een enigszins op te tillen. Stop na enkele minuten de Coachlab meting Exporteer de data voor verdere analyse Bereken de gemeten specifiek warmte van aluminium Vergelijk dit resultaat met de literatuurwaarde (c_Al = 895 J.kg^-1.K^-1).

Experimentele bepaling van de oplossings Enthalpie van Kalikumchloride
Plaats de calorimeter bak op een balans en vul deze met ca. 125 ml water dat op kamertemperatuur gebracht is Noteer de hoeveelheid water die in bewerking genomen is Voeg een roerboon toe Plaats de calorimeter op de roermotor en zet deze aan Stel Coachlab in om elke seconde 1 meting te doen gedurende 15 min Start Coachlab en laat het gedurende minimaal 1 min draaien om de temperatuur van het water te bepalen Weeg ca. 5-10 g KCl af in een bekerglaasjes en noteer de totale massa Giet de KCl over in de calorimeter. Doe dit snel en zorg ervoor dat de thermometer in het water blijft Weeg het b1ekerglaasje en bereken de hoeveelheid KCl dat in bewerking genomen is. Stop de meting na 10-15 min. Exporteer de data voor verdere analyse Bereken de gemeten specifiek warmte van aluminium Vergelijk dit resultaat met de literatuurwaarde (-17.22 kJ.mol^-1).

Resultaten en discussie:

Bepalen van de soortelijke warmte van water
Als warmte toegevoegd wordt aan een vloeistof of een vaste stof dan wordt deze warmte gebruikt om de interne energie van het system te verhogen hetgeen we waarnemen als een temperatuursstijging. De relatie tussen de geleverde warmte en de temperatuur wordt weergegeven door: Q = m.C_p.DT Waarin Q de warmtehoeveelheid is in J/s, m de massa van de vloeistof of vaste stof in kg, C_p de soortelijke warmte van de vloeistof of vaste stof in J/(kg.K) en DT de temperatuursverandering. Volgens de elektriciteitsleer is de warmte die in een weerstand ontwikkeld wordt gelijk aan: DQ = U.I.Dt Waarin DQ de ontwikkelde warmte in de weerstand is in J, U de spanning over de weerstand in V, I de stroomsterkte in A en Dt de tijd dat de stroom loopt. Deze door de weerstand ontwikkelde warmte wordt opgenomen door het water en door de calorimeter. De warmte die door de calorimeter wordt opgenomen is m_c.c_c.DT. De warmte-uitwisseling kunnen we dan uitschrijven als: U.I.Dt = m_w.c_p.Dt + m_c.c_c.DT Op de soortelijke warmte van de vloeistof en die van de calorimeter na kunnen we alle waarde meten. De "soortelijke warmte van de calorimeter" kunnen we echter wel afschatten omdat alleen het aluminium (+ de roerboon) warmte opneemt. Door nu de warmtecapaciteit van Aluminium te nemen kunnen we de warmtecapaciteit van de calorimeter afschatten m.b.v. c_c = m_Al.c_p(Al) [895 J/(kg.K)] = 29.1/1000 * 895 = 26 J/K. Tijdens het experiment meten we de temperatuur in de calorimeter (water) als functie van de tijd. Door deze twee grootheden grafisch uit te zetten ontstaat een rechte lijn met een richtingscoëfficiënt DT/Dt. De soortelijke warmte van de vloeistof in de calorimeter (water) kunnen we hiermee bepalen door de formule van warmte-uitwisseling te gebruiken om de vergelijking van de richtingscoëfficiënt (rc) uit te schrijven: rc= DT/Dt = U.I/(m_w.c_p + m_c.c_c) ==> c_p = (U.I - rc.m_c.c_c)/(rc.m_w) Analyseren we nu de verzamelde data op deze manier dan verkrijgen we onderstaande tabel. Om te kijken of het gebruik van een roerboon invloed zou uitoefenen op de resultaten heb ik een aantal experimenten uitgevoerd zonder roerboon en gebruik gemaakt van de ingebouwde roerder. In de berekeningen voeg ik de massa van de roerboon toe aan de aluminium beker en behandel deze als zijnde aluminium.

Deze eerste resultaten laten een relatief grote afwijking t.o.v. de theoretische waarde zien. Gezien deze onnauwkeurigheid maakt het niet veel uit of men wel of niet gebruik maakt van een roerboon. Een langere opwarmtijd lijkt de meting ook niet nauwkeuriger te maken.
Een van de mogelijke fouten die we in de berekening maken is dat we de warmtecapaciteit van de calorimeter onnauwkeurig bepalen. Om te kijken of ik deze wat beter kon berekenen heb ik twee methodes toegepast. Het gebruik van een afkoelingscurve en het berekenen van de hoeveelheid toegevoegde warmte en de meer officiële methode waarbij we gebruik maken van de warmtecapaciteit van water.

Bepalen van de weerstand van de weerstandsdraad en afschatten van de warmtecapaciteit van de calorimeter.
	Op de calorimeter wordt een waarde van 2-3 Ohm opgegeven. We meten een weerstandwaarde van 2.7 Ohm.

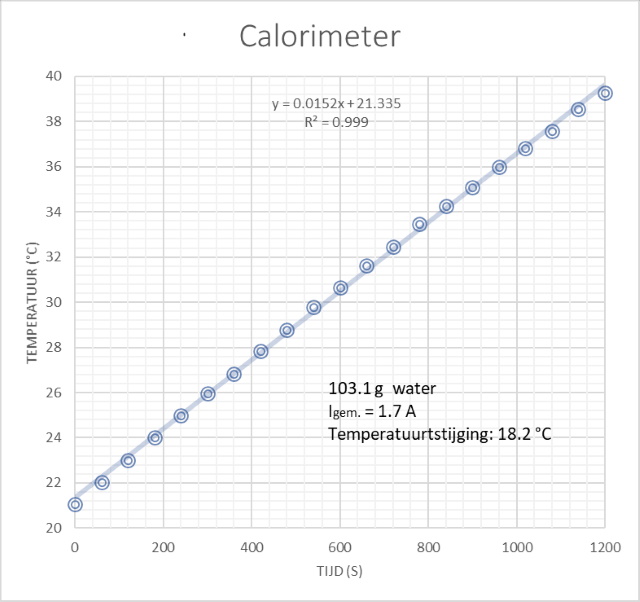
De warmteproductie van een stroom die door een geleider loopt kan berekend worden met de Wet van Joule. Die luidt: Q = P.t = U.I.t = R.I².t Waarin Q de warmteproductie is in J, U de elektrische spanning over de weerstand in V, P het vermogen in J, I de stroomsterkte door de weerstand in Ampère en t de tijd in s. Gedurende 20 minuten opwarmtijd is de warmteproductie met een gemiddelde stroomsterkte van 1.7 A dan: Q = 2.7 * (1.7)² * (2060) = 9396 J. Voor 103.1 g water geeft dat een temperatuursverhoging van: DT = Q/(C_p.m_w) = 9396 / ( 4186 0.1031) = 21.8 °C In werkelijkheid vinden we een temperatuursverhoging van 18.2 °C, een afwijking van 20% relatief.

Kennen we dit verschil toe aan warmteverlies aan de omgeving dan kunnen we met dit verschil de warmtecapaciteit van de calorimeter afschatten nl. Q voor een DT van 18.2 °C = DT.m.C_p =18.2 * 0.1031 * 4186 = 7855 J Verschil = 9364 - 7855 = 1509 J C_cal = 1502 / (21.8 - 18.2) = 417 J/K Een getal dat in eerste instantie veel te hoog lijkt, zeker vergeleken met de eerste afschatting van 26 J/K. Procedureel kan ik zo snel echter geen fout in mijn redenering vinden. Misschien dat het te maken heeft met een verandering van de weerstandwaarde als de temperatuur veranderd, bij hogere temperatuur neemt deze toe. 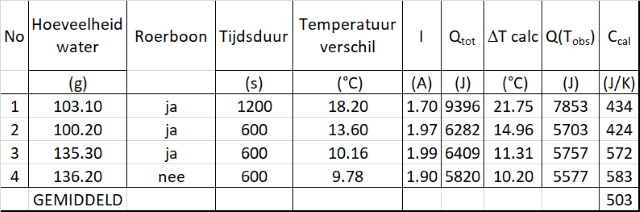Passen we deze methode toe op alle waarnemingen dan krijgen we onderstaande tabel:

Hetgeen bevestigd dat deze methode niet echt geschikt is om de warmtecapaciteit van de calorimeter te berekenen.
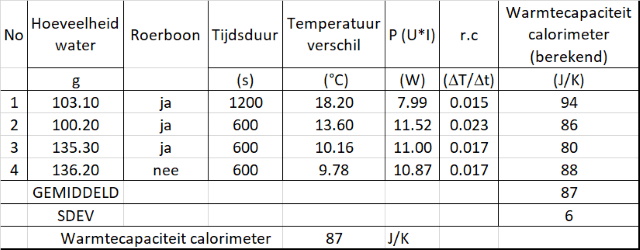
Bij de meer officiële methode gebruiken we wederom de soortelijke warmte van water volgens: U.I.Dt/DT = m_wC_w.DT + C_cal.DT==> C_cal = P/r.c. - C_w.m_w Dan verkrijgen we onderstaande tabel.

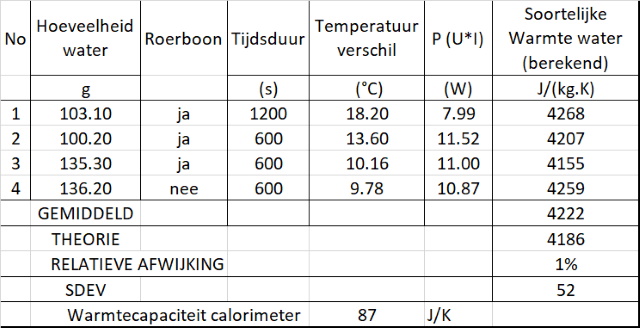
Dat lijkt een meer realistisch getal te zijn, meer in lijn met de eerdere schatting en meer in lijn met wat men in de literatuur vindt. Gebruiken we deze gemiddelde waarde om de warmtecapaciteit van water te berekenen dan krijgen we onderstaande tabel:

Al met al geeft deze methode tot op dit moment wel een beetje een wceend gevoel (Wij van WC eend adviseren WC eend) en ik vroeg me dus af of ik de afkoelingscurves kon gebruiken om tot een betere afschatting van de warmtecapaciteit van de calorimeter te komen. Na wat nadenken moest ik echter concluderen dat ik er niet onderuit kwam om wederom de soortelijke warmte van water te gebruiken, hetgeen mijn probleem dus niet oploste. Een andere manier om te bepalen of men de warmtecapaciteit van de calorimeter enigszins goed bepaald heeft is door de soortelijk warmte van een ander materiaal te bepalen zoals bv. Aluminium

Experimentele bepaling van de soortelijke warmte van aluminium

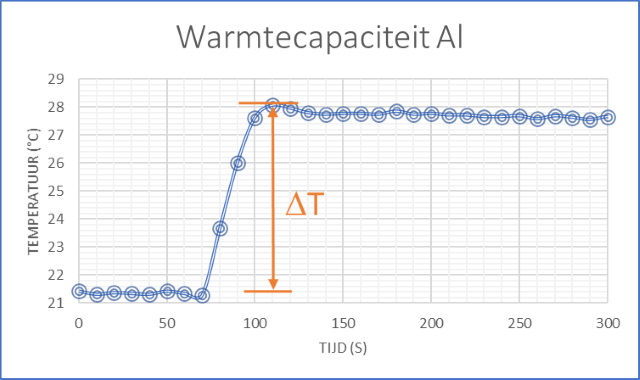
We hebben het experiment twee keer uitgevoerd met hetzelfde blok Aluminium van 65.1 g. In Exp 1 is 120.5 g water in behandeling genomen en in Exp 2 124.3 g water. In onderstaande grafiek wordt het resultaat van het tweede experiment getoond.

Als men het blok Aluminium in de calorimeter plaatst zullen de calorimeter en het water warmte opnemen terwijl het blok warmte zal afgeven. De opgenomen warmte: Q_op = Q_H2O + Q_cal = m_w.C_w.DT + C_cal.DT (J) Hierin is DT het temperatuurverschil zoals waargenomen in bovenstaande grafiek (T_max-T_min) De afgegeven warmte: Q_af = Q_Al =m_Al.C_Al.DT_Al(J) Hierin is DT_Al het temperatuurverschil van het Al blok op het moment dat het in de calorimeter geplaatst werd (100 °C) en de maximale temperatuur zoals waargenomen in bovenstaande grafiek. Aangezien: Qop = Qaf Kan me de soortelijke warmte van Aluminium berekenen volgens: C_Al = Q_op/(m_Al.DT_Al) J.(kg.k) De resultaten zijn samengevat in onderstaande tabel.

Een mogelijke verklaring voor het waargenomen verschil is dat het Aluminium blokje al een beetje afgekoeld is als men het in de calorimeter plaats. De temperatuur zal iets onder de 100 °C liggen. Dat dit een redelijke aanname is blijkt als we het even narekenen met een temperatuurdaling van 3 °C van het Aluminium.


Experimentele bepaling van de oplossings Enthalpie van Kaliumchloride
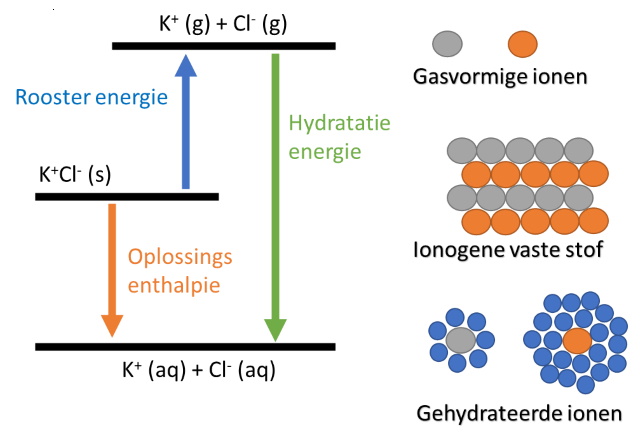
Om een zout waarvan de ionen vast zitten in een ionogeen rooster op te lossen moeten de ionbindingen verbroken worden. Dat betekent dat de roosterenergie in het systeem ingevoerd moet worden, een endorherme reactie, waarna de ionen gesolvateerd worden door de oplosmiddel moleculen, hetgeen zowel een endotherme als een exotherme reactie kan zijn. Deze clusteren rondom de ionen.

De kristallisatie enthalpie van KCl is -715 kJ/mol. De hydratatie enthalpie van kalium en chloride ionen zijn respectievelijk -322 en -363 kJ/mol. De hydratatie enthalpie van KCl is dan: ΔH_hyd=−322+(−363)=−685kJ/mol De oplossings enthalpie is dan: ΔH_sol=−685−(−715) = 30 kJ/mol Bij een endotherme reactie is ΔH_sol positief, bij een exotherme reactie negatief. Men meet een temperatuurverandering t.o.v. de omgeving op basis waarvan de de warmte-uitwisseling berekend wordt. De Enthalpie heeft het tegenovergestelde teken van de berekende energie. DH = -Q Q berekenen we in dit experiment wederom met de formule: Q = m.C_p.DT Hierin is: m = massa water + massa zout (kg) C_p = soortelijke warmte water (4180 J/mol) De solvatatie energie brekenen we dan volgens: ΔH_sol= - Q/ n Hierin is: n = mol KCl in bewerking genomen
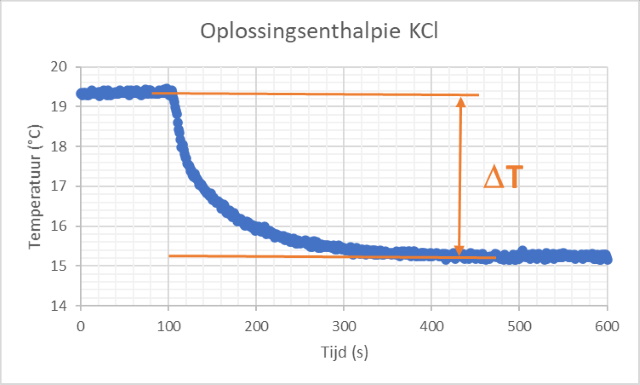
Onderstaande grafiek is een grafische weergave van een van de twee uitgevoerde metingen.

In onderstaande tabel zijn de resultaten samengevat.

De theoretische waarde die hier geciteerd wordt komt uit het artikel van Kilday. Men kan zichzelf onmiddellijk twee vragen stellen. 1. Kunnen we het verschil tussen meting en theorie verklaren? 2. Kunnen we het verschil tussen de door ons berekende waarde en de waarde opgegeven in de literatuur verklaren?
In bovenstaande berekening was de warmte capaciteit van de calorimeter nog niet meegenomen. Als we dat wel doen verkrijgen we onderstaande tabel:


De afwijking met de literatuur is iets kleiner geworden maar wijkt nog steeds ca. 5 % relatief af. Er zijn nog wat andere foutenbronnen die een bijdrage aan de afwijking kunnen leveren, zoals b.v.: 1. De KCl in niet echt zuiver, we hebben brouwzout gebruikt hetgeen niet van p.a. kwaliteit is. 2. Variaties in de deeltjesgrootte beïnvloeden de snelheid van oplossen hetgeen een uitsmerend effect kan hebben. 3. Concentratie effecten kunnen een rol spelen. Meestal gaat men in de literatuur uit van oneindig verdunde oplossingen.
Waar ik het meeste mee worstel is het verschil tussen de literatuur/meet waarde en de theoretisch berekende waarde, dat scheelt bijna een factor 2.
Een van de mogelijke verklaringen waar ikzelf aan zat te denken is dat het vormen van een watermantel rond een ion bepaald wordt door de ladingsdichtheid van de ionen en wat dat betreft scoren zowel kalium als chloride ionen slecht. Ik heb echter geen uitgespitte verklaring kunnen vinden die dit verschil goed verklaart.

Conclusies:

De warmtecapaciteit van de calorimeter is bepaald als zijnde 87 J/K
De ("gecorrigeerde") soortelijke warmte van Aluminium is bepaald als zijnde: 899 J/(kg.K) (Literatuur: 895 J/(kg.K))
De gemeten oplossings enthalpie van kaliumchloride is 18.4 kJ/mol, een waarde die ca. 5% relatief afwijkt van de literatuur (17.58 kJ/mol)

Opmerkingen:

Bij mij staat dit instrument nog bekend als een calorimeter. Tegenwoordig spreekt men echter ook wel van een Joulemeter. Pro-forma was deze naamswijziging echter niet nodig. Het woord calorimeter betekent warmtemeter en heeft niets te maken met de eenheid calorie.
Let erop dat de weerstanddraad (de spiraal) geheel onder water komt. Dan kan deze de warmte maximaal overbrengen en tevens voorkomt men dat de draad oververhit raakt.
De Coachlabfiles:
Calorimeter
Calorimeter2
Calorimeter3
De Excel file: calorimeter exp 032020
Men kan het rekenwerk ook in CoachLab uitvoeren maar ik vind het voor mezelf gemakkelijker om in Excel te werken.

Literatuur:

O.G. Brink en R.J. Flink; "Algemene Instrumentenkennis"; Wolters-Noordhoff; 1971; ISBN 9001162509; p. 24,25.
Ir. J.T. van Konijnenburg; "Natuurkunde Zien en Doen"; Elsevier (Heron); 1973; ISBN 9010104354; p. 216-218.
J.A. Tijmens, B. Taken; "Natuurkunde voor het MLO 1"; Heron; 1986; ISBN 9031307637; p.106-113.
P. Doornenbal, F.W. Nijhof, P.J. Gathier; Natuurkunde-A; 26ste druk; Tjeenk-Willink; 1960; ;p. 98-102.
W.H. Wetphal; "Physikalisches Praktikum"; 9de druk; Friedr. Vieweg & Sohn; 1959; p. 78-81.
E. Brian Smoth; "Elementaire Chemische Thermodynamica"; Heron; 1989; ISBN 9031309966; p. 9-19, 77-86.
J.W. Middelink, F.J. Engelhard; "Systematische Natuurkunde voor bovenbouw vwo B^-2"; Van Walraven; 1992; ISBN 9060498240; p. 255-259.
V.L. Lechtanski; "Inquiri-Based Experiments in Chemistry"; Oxford University Press; 2000; ISBN 0841235708; p. 43-128.
Binas; Wolters-Noordhoff; 1992; ISBN 9001893724; Tabel 10-12.
M.V. Kilday; "The Enthalpy of Solution of SRM 1655 (KCl) in H₂O"; Journal of Research of the National Bureau of Standards; 1980 6 85; p. 467-481.

Relevante websites:

Minder relevante websites:

Warmtecapaciteit van een Joulemeter

Achtergrondinformatie:

Bepalen van de hoeveelheid warmte

Willen we iets te weten komen over de hoeveelheid warmte die vrijkomt bij of nodig is voor een proces, dan gebruiken we een calorimeter. Een calorimeter is een toestel waarbij de warmte-uitwisseling met de omgeving tot het uiterste wordt beperkt. Zo wordt er voor allerlei bepalingen (soortelijke warmte, verdampingswarmte, smeltwarmte, etc.) gebruik gemaakt van een calorimeter. In principe kan men reeds warmte meten mbv een metalen bakje met een dunne wand. Dit bakje wordt dan op een laagje plastic gezet. In het bakje worden een thermometer en een roerder geplaatst. Verder is het bakje met water gevuld. Door het water te roeren wordt ervoor gezorgd dat de temperatuur overal in het bakje gelijk is. Een laboratorium calorimeter lijkt erg veel op bovenstaande opstelling er zijn echter een paar belangrijke verschillen. Het belangrijkste onderdeel is een koperen bak. Deze bak is omgeven door een tweede bak, zodat er een isolerende luchtlaag ontstaat hetgeen resulteert in een minimum aan warmte-uitwisseling met de omgeving. Daarom is de binnenste bak een laag kurk geplaatst en is het geheel afgeschermd door een deksel van perspex, waardoor een thermometer en een roerder kunnen worden gestoken. De roerder heeft de vorm van een ring zodat bij het op en neer bewegen de vloeistof tot stroming wordt gebracht. Hierdoor vindt er een snelle en gelijkmatige warmteverdeling plaats. Daar de calorimeter, de thermometer en de roerder, bij menging van twee stoffen van verschillende temperatuur, temperatuurveranderingen ondergaan , moet het aantal Joule dat de calorimeter met toebehoren, per graad temperatuurstijging opneemt (dit is de warmte capaciteit van de calorimeter) bepaald zijn. Bij het verrichten van metingen met de calorimeter moet er op toegezien worden dat de begin- en eindtemperatuur van de calorimeter zo worden gekozen, dat deze symmetrisch liggen t.o.v de. kamertemperatuur. Dit om eventuele warmte-afgifte aan en warmte-opname van de omgeving zoveel mogelijk aan elkaar gelijk te maken, waardoor de hierdoor optredende fout zo klein mogelijk wordt gehouden.

De warmteafgifte of warmteopname q naar of van een massa m is gerelateerd aan de te temperatuursverandering DT volgens: q = Cp.m.DT waarbij Cp de specifieke warmte capaciteit van die massa is bij constante druk.

Voor water: Cp = 4.18 J/(g.°C)

16/05/2020