Parallelle Plaat Condensator

Parallele Plaat Condensator onderzoeken

Datum: Augustus - September 2020

Inleiding:

Een zelfgemaakte condensator onderzoeken met verschillende meetinstrumenten.

Materiaal:

Oude CD's of DVD's
Duct Tape
Aluminium folie
Snijmes
Multimeter (Velleman )
USB Oscilloscoop (RockTech)
Striptang
Lijm
Plakband
Kabel
Soldeerbout en soldeertin
Kabels met krokodillenklemmen
Weerstand 10 kOhm
Set gewichten
A4 papier en/of folie (overhead sheets)
Zwaar boek
Micrometer
Ouderwetse trim-condensator

Uitvoering:

Capaciteits onderzoek:
Neem een vel A4 papier en een strook alufolie groter dan A4 Gebruik het A4 als mal en snij een stuk Alufolie uit op A4 formaat met een kleine extra strip op het uiteinde aan de lange zijde Maak een tweede vel alu folie op dezelfde manier Neem een vel A4 papier of een vel folie (cellofaan) en leg dit tussen de alufolie De alufolie moet zo geplaatst zijn dat de uitstekende delen aan een kant aan beide zijden zit De alufolie delen behoren elkaar niet te raken Leg een zwaar boek op de alufolie Verbindt de multimeter aan beide delen en meet de capaciteit Voeg steeds een vel cellofaan toe en doe vervolgens een meting van de capaciteit Vouw de beide vellen eenmaal op tot formaat 1/2 A4. Leg ze op elkaar met een enkel vel cellofaan ertussen en meet wederom de capaciteit Vouw nogmaals op (1/4 A4) en herhaal wederom de metinng met 1 vel cellofaan ertussen Bepaal de dikte van een vel cellofaan m.b.v. een micrometer


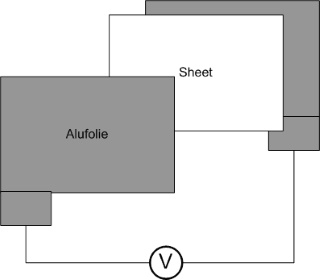Capacitieve weegschaal:
De duct tape kan men gebruiken om de opdruk van de CD's te vewijderen door deze erop te plakken en eraf te trekken. Gebruik een CD als mal en snij voorzichtig een cirkelvormig stuk alufolie uit. Plak dat alufolie vast op de CD. Herhaal dit proces met een andere CD Neem een stuk draad en strip beide uiteindes. Spreid de draad uit aan een kant plaatse deze op de alufilie en zet deze met plakband vast aan de CD. De draad aan de andere kant kan men verstevigen met een beetjke soldeertin Plaats beide CD 's op elkaar met de alufolie kant naar elkaar toe, maar zet er een niet beplakte CD tussen, zodat de alufolies elkaar niet raken. Verbind de draden met de multimeter.	Zet de multimeter op CAP (Capacitance) meting. Noteer de af te lezen waarde. Plaats nu verschillende gewichten op de CD en noteer de meetwaardes
	Gewichten plaatsen
Capacitieve weegschaal met Oscilloscoop:
Een herhaling van het vorige experiment maar nu met een oscilloscoop en een variabele voedingsbron. Bouw de meting op volgems nevenstaand schema met de oscilloscoop geschakeld over de 10 kOhm weerstand Stel de toongenerator in op 10 kHz Meet met en zonder gewicht Vergelijk de oscilloscoop signalen


Capaciteitsonderzoek met de CD's:
De gestripte en beplakte CD's die we in de vorige experimenten gebruikt hebben kunnen we ook gebruiken om het effect van afstand tussen de platen te onderzoeken.
Begin het experiment met slecht een plastic CD tussen de platen Verbind de platen met de multimeter Plaats een gewicht Meet de capaciteit Herhaal het experiment waarbij men steeds 1 plastic CD extra tussen de platen plaatst. Bepaal de dikte van de plastic CD's met een micrometer.

Trimcondensator:
Neem een trimcondensator en verbindt deze met de multimeter Stel deze in op het meten van de capaciteit Draai aan de rotor van de trimcondensator Observeer Maak evt. een filmpje

Resultaten:

Capaciteits onderzoek:
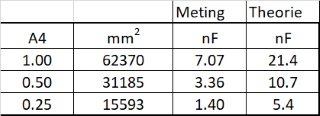
In onderstaande tabel worden de meetwaardes weergegeven.

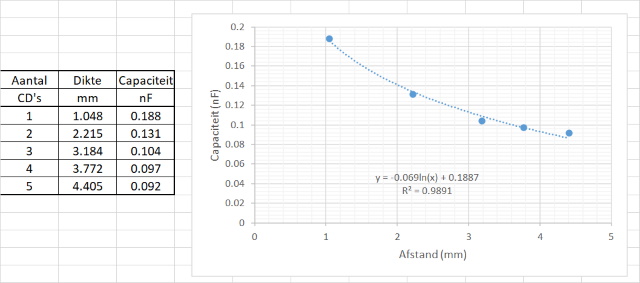
Deze worden vervolgens grafisch weergegeven. Men kan waarnemen dat de capaciteit lineair toeneemt met toenemend oppervlak en logaritmisch afneemt als functie van de aftand tussen de platen.



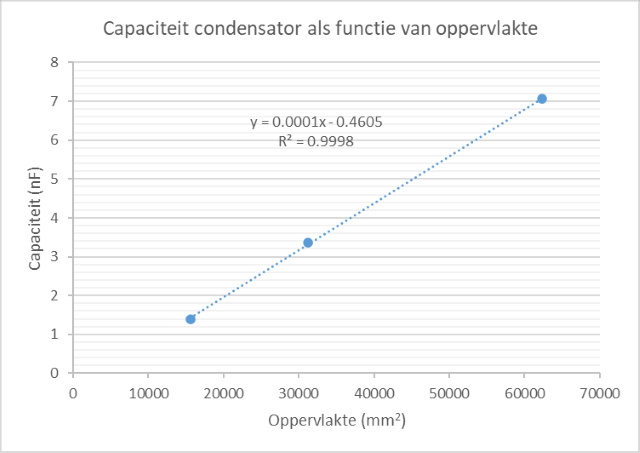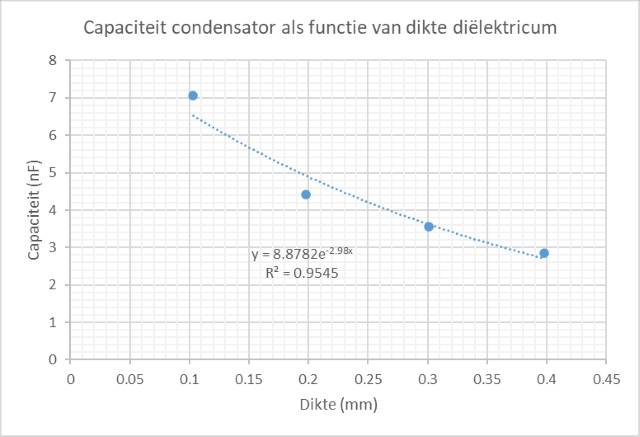Capacitieve weegschaal:
De meetresultaten laten zien dat de capaciteit toeneemt als het gewicht toeneemt.


Capacitieve weegschaal met Oscilloscoop:
Op de oscilloscoop kan men waarnemen dat door een gewicht te plaatsen de amplitude toeneemt.

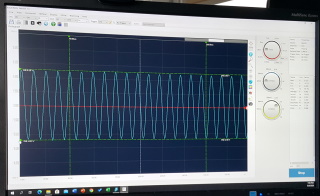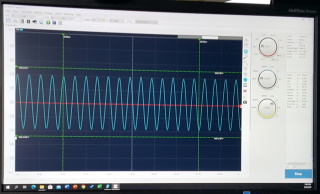Met Gewicht	Zonder Gewicht

Capaciteitsonderzoek met de CD's:
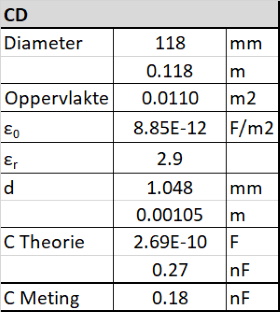
De resultaten laten zijn de capaciteit logaritmisch afneemt als de dikte toeneemt.


Trimcondensator
Variabele of trim condensatoren worden gebruikt in toepassingen waar het nodig is om een regelbare capaciteit te hebben. Dit soort variabele condensator wordt meestal trimmer genoemd. De meest voorkomende vorm regelt een groep halfronde metalen platen op een rotatieas ( "rotor") die zijn gepositioneerd in de ruimte tussen een stel stationaire platen ( "stator"), zodat het overlappingsgebied kan worden gewijzigd door draaiing van de as. Lucht of kunststof folies kan worden gebruikt als diëlektrisch materiaal. Door keuze van de vorm van de roterende platen kunnen verschillende functies van de capaciteit versus hoek worden gemaakt, bijvoorbeeld een lineaire frequentieschaal verkrijgen.
YouTube link: Trim condensator

Discussie:

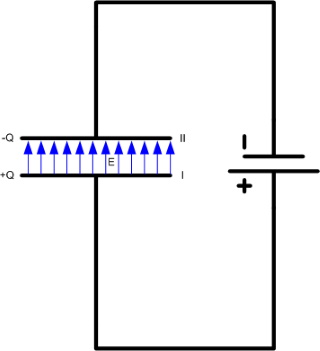
Voor de elektrische veldstrekte in een homogeen elektrisch veld gaat men uit van twee vlakke geladen platen die op een korte afstand van elkaar staan. De elektrische veldlijnen staan loodrecht op beide platen en verlopen tussen de platen evenwijdig aan elkaar. Brengen we op plaat I een positieve lading +Q (eenheid: Coulomb) aan dan zal, indien plaat II met de aarde verbonden is, door influentie op plaat II dezelfde negative lading -Q ontstaan. De twee ladingen oefenen aantrekkende krachten op elkaar uit, waardoor de lading van I zich geheel op de naar II gekeerde kant van de plaat bevindt en omgekeerd. De flux Ψ die van de lading +Q van plaat I uitgaat komt geheel op de binnenzijde van plaat II bij de lading -Q terecht (bij benadering, bij een zeer geringe afstand tussen de platen). Voor de flux Ψ kunnen we schrijven: Q = Ψ = D.A = ε . E. A Hierin is A het oppervlak van een kant van de plaat. Voor de elektrische veldsterkte geld dan: E = Q /(ε . A)
Voor de elektrische verplaatsing: D = Q/A Hierin is D de ladingsdichtheid, de lading per oppervlakte-eenheid. Ieder samenstel van twee tegenover elkaar geplaatste geleiders, gescheiden door een isolerend medium (dielektricum) noemen we een condensator. Stellen we de lading op een van de geleiders voor als Q en het potentiaalverschil tussen beide geleiders als U dan kunnen we stellen: C = Q/U --> Eenheid: C/V = F (Farad) C oftwel de capaciteit, is afhankelijk van de geometrische verhoudingen van de geleidende oppervlakken en de aard van het medium dat de oppervlakken scheidt. In een homogeen elektrisch veld word de relatie tussen de elektrische veldsterkte E en het potentiaalverschil U tussen de condensatorplaten weergegeven door: E = U/d (hierin is d de afstand tussen de platen in m) Voor de capaciteit van de vlakke condensator geldt dan: C = Q/U = (ε . A)/d (hierin is A het oppervlak in m²) Deze formule wordt dan verder uitgeschreven als: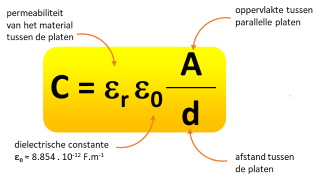
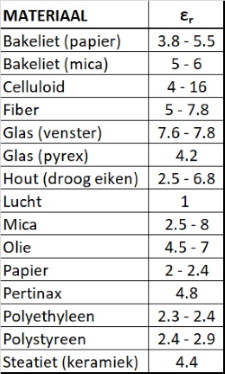
Waarvoor geldt: ε = overall dielectrische constante ε₀ = absolute dielectrische constante (in het luchtledige) ε_r = relatieve dielectrische constante De relatieve dielectrische constante van verschillende materialen is weergegeven in nevenstaande tabel. De dielectrische constante van polycarbonaat (CD) is 2.9. Gebruiken we nu deze getallen om de de theoretisch capaciteit te berekenen en te vergelijken met de meetwaardes dan kunnen verkrijgen we de volgende waardes.
Alufolie met cellofaan	CD met polycarbonaat
Globaal zien we een factor 2-3 verschil tussen meetresultaat en de berekende waarde in de uitgevoerde experimenten. Een verschil dat we niet kunnen verklaren door een onnauwkeurigheid in de oppervlaktebepaling aan te nemen. Ik vermoed dat twee factoren hier een rol spelen. De eerste factor is de aanname welke dielectrisch contante we gebruiken in de berekening. Ik heb niet de tools om te controleren of ik de juiste materiaalkeuze gemaakt heb.
In de tabel kunnen we ook zien dat de dielectrische constante van veel plastic soorten een range beslaat, hetgeen automatisch een onnauwkeurigheid introduceert. Bij de CD's geld ook dat er een gat in het materiaal zit, dus een deel is niet polycarbonaat maar lucht. De tweede factor die volgens mij een verschil maakt is de afstand tussen de condensatorplaten. We bepalen welliswaar de dikte van het materiaal met een micrometer, maar de materialen die we gebruiken zijn nogal zacht. Als we er een gewicht op plaatsen zal het materiaal een beetje deformeren, minder dik worden. Nu is het wel zo dat de afstand tussen de condensatorplaten in de noemer van de vergelijking staat dus we zouden verwachten dat het verschil tussen theorie en praktijk kleiner wordt, alhoewel het in deze context waarschijnlijk beter is om te zeggen dat het verschil minder groot geworden is.
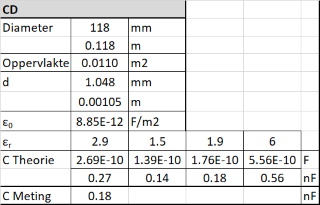
Een andere onnauwkeurigheid waar we mee te maken hebben is de nauwkeurigheid van de multimeter (Velleman DVM9912). Volgens de handleiding is die ca. 5%, onvoldoende om de verschillen tussen theorie en praktijk mee te verklaren. Al met al houden we op basis van deze redenatie alleen maar de onnauwkeurigheid in dielectrische constante over om het verschil tussen theorie en praktijk te verklaren. Een numerieke exercitie, waarvan de resulaten zijn weergegeven in nevenstaande tabel levert enige onderbouwing voor deze redenatie.
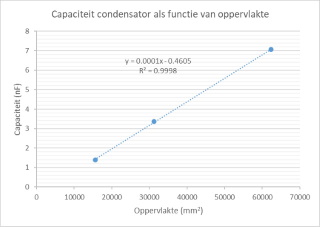
Capaciteit van de condensator als functie van oppervlakte
Als we naar bovenstaande capaciteitsformule kijken dan kunnen we herkennen dat de capaciteit recht evenredig verloopt met het condensator oppervlak. Dat kunnen we inderdaad waarnemen in het uitgevoerde experiment.
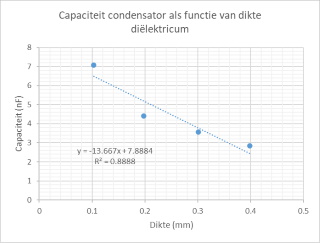
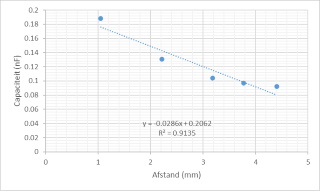
Capaciteit van de condensator als functie van de dikte van het dielectrum
Volgens dezelfde formule verloopt de capaciteit omgekeerd evenredig met de afstand tussen de condensator platen. De afname kunnen we inderdaad duidelijk waarnemen maar de lineariteit is minder duidelijk waarneembeer. In eerste instantie denkt men dan dat men de experimenten niet goed uitgevoerd heeft maar met wat spitten op het internet kan men zien dat dit soort resultaten wel vaker gevonden worden. De uitzondering is als het experiment strakker uitgevoerd wordt met platen waarbij men op een balk de positie nauwkeurig kan meten en fixeren. Dat laat mij vermoeden dat de reeds vermelde reden van de onnauwkeurigheid van de dikte/afstandbepaling van de gebruikte materialen hier een grote rol spelen en een grotere variatie veroorzaken.
Capacitieve weegschaal
De amplitude van de spanningsval over de weerstand R is evenredig met de amplitude van de wisselstroom. Deze wordt bij een constante frequentie en amplitude van de generatorspanning bepaald door de capaciteit van de twee platen t.o.v. elkaar. Belast men de condensatorplaten (weegschaal) dan wordt de afstand tussen de condensatorplaten kleiner en de capaciteit van de condensator groter. De stroomamplitude neemt dan toe zoals men op het oscilloscoopscherm kan waarnemen.
Trimcondensator
In het experiment met de trimcondensator kan men waarnemen dat als de afstand tussen de platen kleiner wordt de capaciteit toeneemt.

Conclusies:

Volgens verwachting laten de experimenten zien dat de capaciteit van een condensator:

Evenredig toeneemt als functie van het oppervlak van de condensatorplaten
Afneemt als de afstand tussen de condensatorplaten toeneemt.

Literatuur:

A.C.J. Berens, A.W.N. Kerkhofs; "101 Proeven met een oscilloscoop"; Kader reeks; 1966
R.J. Flink; "Elektriciteitsleer"; Nijgh & Van Dirmar; 1992; ISBN 9023606736; p. 65-113.
T.T. Grove, M. F. Master, R.E. Miers; "Determining dielectric constants using a parallel plate condensator"; American Journal of Physics; 73 52 2005; p. 52-56.

Relevante websites:

Minder relevante websites:

Opmerkingen:

De resulaten zijn opgeslagen in de Excel file: resultaten

Achtergrondinformatie:

In elektronische schakelingen wordt een condensatorgebruikt om elektrische lading op te slaan, waarna het ook als een tijdelijke spanningsbron kan dienen (bv voor de startmotor van een auto) en om frequenties te filteren.

Als een gelijkspanning op een condensor aangesloten wordt dan vloeit er een elektrische stroom totdat de condensator volledig is opgeladen, op dat punt fungeert de condensator als een blokkade en vloeit er geen stroom meer. Bij wisselspanningen daarentegen wordt een condesator voortduren op- en ontladen waardoor er een "schijnbare" condenavindt een stroom vloeit. De elektrische weerstand dneemt af als de frequentie van de wisselstroom toeneemt.