Nauwkeurigheid van een zandloper

Datum:  Augustus 2020

Inleiding:

In een Reddit post kwam ik dit experiment tegen. Ik bedacht met dat ik het met Coachlab kon uitvoeren.

Materiaal:

  • CMA Coachlab II
  • CMA Lichtsensor (0513)
  • Zandloper
  • Laser(pointer)
  • Lego
  • Klemmen
  • PC met Coachlab software en Excel
  • Laboratorium platform
  • Oude schoenendoos
    •

 


Laserwaterpas
 


Coachlab II Interface
Lichtsensor

Uitvoering:

  • Bouw de opstelling op zoals weergegeven ion onderstaande foto
  • Gebruik de lego stukken om een houder te bouwen waarbij zowel de laserwaterpas als de zandloper steeds op dezelfde positie geplaatst worden
  • Plaats de opstelling in de schoenendoos
  • In dit experiment maken we gebruik van een 3 minuten zandloper.
  • Bouw de opstelling op binnen een schoenendoos of vergelijkbaar
  • Stel Coachlab in op een tijdsuur van 5 minuten met 2 metingen per seconde
  • Start de meting en draai dan pas de zandloper om
  • Plaats het deksel op de schoenendoos
  • Positioneer deze nauwkeurig
  • Exporteer de meting
  • Herhaal de meting diverse (vele) malen om een statistisch significante dataset te verkrijgen
  • Let erop dat men de zandloper ook omdraait na elke meting zodat we "beide zandloop kanten" van de zandloper in het experiment representatief meenemen
  • Importeer de meetdata in Excel en analyseer de verkregen dataset
    •
 

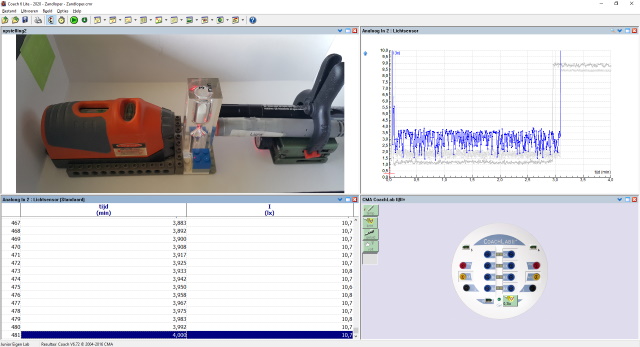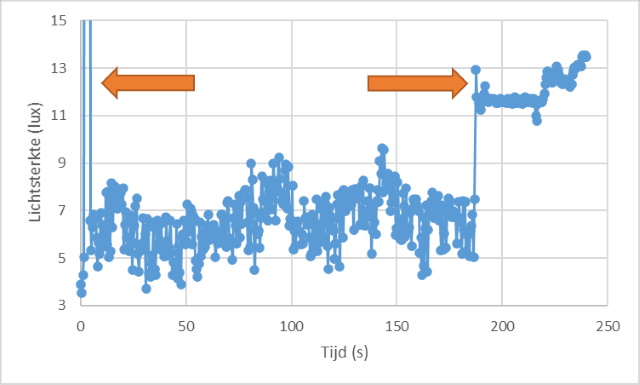
Resultaten:

Meting:

YouTube link: Zandloper meting



  • Zet elke meting grafisch uit en bepaal het begin en eindpunt van de zandstroom zoals aangegeven in onderstaande grafiek.
 


  • Bereken de verlopen tijd tussen begin en eind en verzamel alle data in een tabel
  • Analyseer de verzamelde data
    •



  • Voor analyse is het gemakkelijker om alle data in een enkele kolom te plaatsen.
  • De resultaten zijn in onderstaand staafdiagram grafisch weergegeven
  • Bereken gemiddelde (=AVERAGE(C3:C57)) en standaardeviatie (=STDEV.S(C3:C57))
  • De resultaten zijn:
    Gemiddelde: 178.5 s
    Standaardeviatie (s): 5.4 s
  • De standaardafwijking of standaarddeviatie (vaak aangeduid met de Griekse letter ? voor de populatie en s voor de steekproef), is een maat voor de spreiding van een variabele of van een verdeling of populatie.
    •


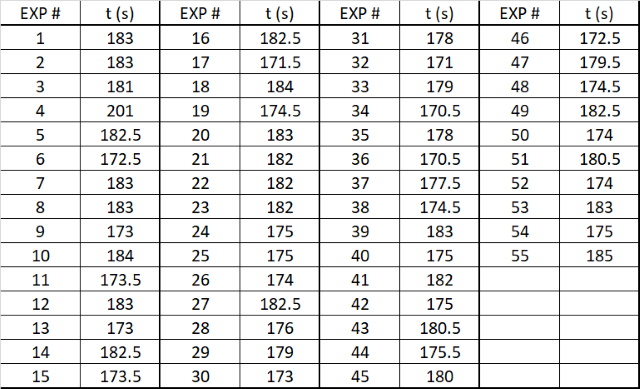
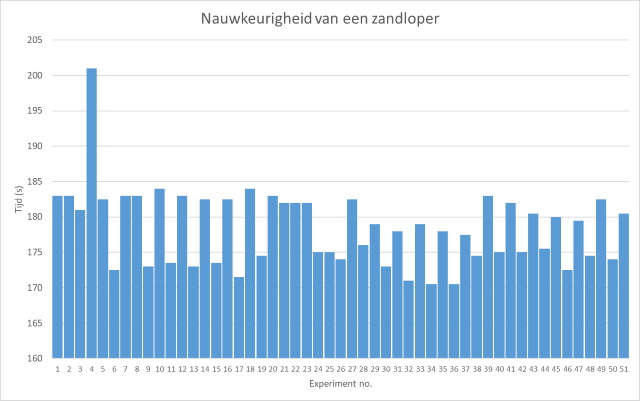
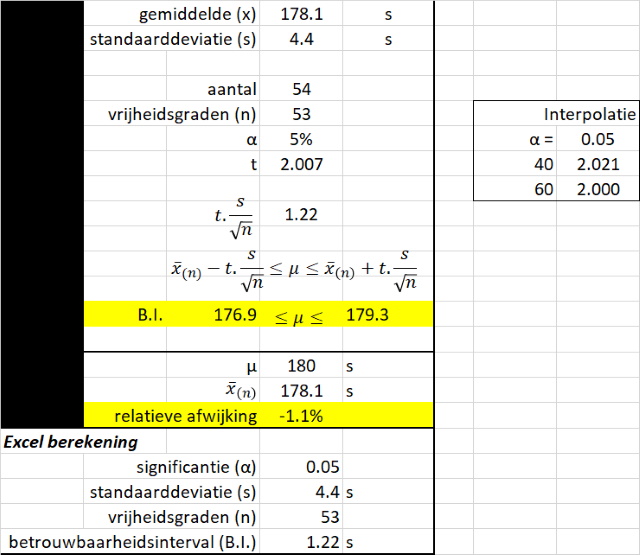
We kunnen aan de resultaten zien dat Exp 4 een uibijter is hetgeen bevestigd wordt als we het experiment nader bekijken. Er is nogal gerommeld tijdens dit experiment. Verwijderen we deze meting dan krijgen we als resultaten:
Gemiddelde: 178.1 s
Standaardeviatie (s): 4.4 s

Gebruiken we deze resultaten voor een statistische analyse waarbij we het 95% betrouwbaarhewidsinterval uitrekenen dan krijgen we onderstaande resultaten.


Bovenstaande berekening is grotendeels met de hand uitgevoer. Zoals ook getoond biedt Excel ook een fucntie voor het uitrekenen van het betrouwbaarheidsinterval m.b.v. CONFIDENCE.T(alpha,standard_dev,size).

Discussie:

Zandlopers zijn voorwerpen die ons aanspreken, het zijn echter geen instrumenten gechikt voor een nauwkeurige tijdswaarneming. De meeste hebben een nauwkeurigheid van ca. 10%. Als men een grotere nauwkeurigheid wil zal men de zandloper nauwkeurig moeten calibreren.


Er zijn verschillende factoren die de nauwkeurigheid van een zandloper bepalen.

  • De hoeveelheid of het volume van het gebruikte zand
  • De grootte en de hoek van het glazen reservoir
  • De kwaliteit van het gebruikte zand of gelijksoortig granulair materiaal.  Het moet fijn, droog en gelijkvormig zijn in vorm en grootte zodat het gelijkmatig kan vloeien (In het verleden gerbuikte men ook wel verpoederde eischaal en verpoederd marmer)
  • De breedte van de nek
  • Een goede afdichting zodat er geen vocht kan binnendringen in de reservoirs. Vocht kan gewicht toevoegen aan het zand en zo de nek verstoppen
  • Een vlak en horizontaal oppervlak waarop men de zandloper kan plaatsen

De resultaten die we gevonden hebben impliceren dat deze zandloper redelijk nauwkeurig is.

Conclusies:

  • De gebruikte zandloper toont een gemioddeld tijdsverloop van 178 s aan, een verschil van -1% relatief t.o.v. de aangegeven 3 minuten (180 s) waarde.
  • Het 95% betrouwbaarheidsinterval van deze metingen is: 1.2 s

Opmerkingen:
  • Om extra lichtinval te beperken zou men de opstelling ook in een schoendoos kunnen plaatsen. Hetgeen ik uiteindelijk ook gedaan heb.
  • De Coachlab file: Zandloper.cmr 
  • De resultaten kan men vinden in de Excelfile: Resulaten
  • In Excel selecteer binnen een kolom de getallen en klik onder DATA op "Text to Columns"
    Herhaal dit ook voor de tweede kolom
    Als je per ongeluk de decimale separator verkeerd heb ingesteld gebruik dan eerst Find and Replace (, naar . of vice versa)
  • De Excel formule STDEV.S() berekent de standaarddeviatie. De .S achter STDEV laat Excel weten dat het hier om een steekproef gaat.
  • Het idee om dit expoeriment uit te voeren heb ik uit een Reddit post, zie de literatuur.

Literatuur:

  • A. A. Mills, S. Dahy, S. Parkes; "Mechanics of the sandglass"; Eur. J. Phys. ; 17 1996 ; p.97-109.
  • Jacques Duran; "Zand in beweging"; Veen; 2008; ISBN 978908571153; p. 1-9.
  • P. Booster; "Statistische methoden voor het laboratorium"; Heron; 1972; ISBN 9010103811.

Relevante websites:

Minder relevante websites:

Achtergrondinformatie:
  Ter illustratie een foto van een grote zandloper die ik in mijn bezit heb.