Hydrostatische Druk

Datum:  November 2021

Inleiding:

Typisch zo'n experiment dat ik altijd al eens wilde doen.

Materiaal:

  • PC met Coachlab software
  • CMA Coachlab II+
  • Druksensor (Vernier GPS-BTA)
  • Statief
  • Maatcylinder (250 ml)
  • Vat
  • Trechter
  • Sluitringen / Moeren
  • Flexibele slang
  • Water
  • Lineaal
  • Hydrostatische druk demonstratie maatcylinder of een vat of cylinder met gaten op verschillende hoogtes
  • Lekbak


Uitvoering:

Meten van de waterdruk
  • Snijd de slang op een lengte die iets langer is als de cilinder.
  • Plaats sluitringen en moeren op de steel van de trechter
  • Verbindt een uiteinde van de slang met de trechter
  • Verbindt het andere uiteinde van de slang met de druksensor
  • Vul de cylinder met water
  • Dompel de trechter in de buis tot een afstand van ca. 4 cm onder het wateroppervlak
  • Meet de afstand tussen wateroppervlak en lucht in de slang
  • Start Coachlab op en noteer de druk en de diepte in cm
  • In Coachlab heb ik de meting "Event Based" uitgevoerd. Bij elke meting kan men dan de diepte opgeven
  • Verlaag de trechter in het water met wederom ca. 4 cm
  • Noteer wederom de meetresultaten.
  • Voer de metingen op verschillende hoogtes uit: 0 cm, 4 cm, 8 cm, 12 cm, 16 cm, and 20 cm
  • Herhaal dit experiment met een cilinder met een grotere diameter
  • In de grote cylinder kan men de trechter maar tot 12 cm laten zakken

 

 Demonstratieproef
  • Zet de cilinder met de gaten in een lekbakje
  • Vul de cylinder met water
  • Observeer


Resultaten:

Screenshot Coachlab gedurende de meting
Meetresultaten in tabel vorm
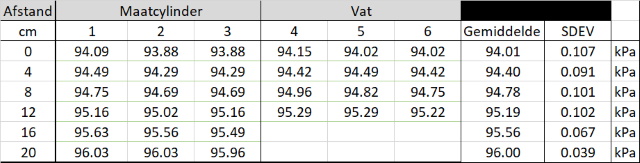Meetresultaten grafisch weergegeven
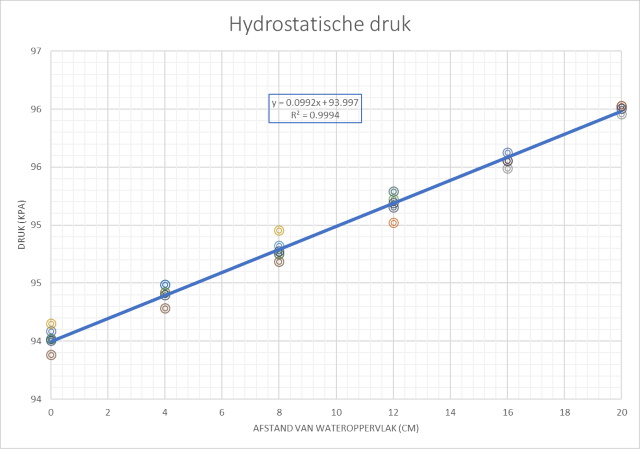Demonstratieproef

YouTube link: Waterdruk demonstratie


Discussie en conclusies:
Een volume vloeistof dat blootgesteld is aan de zwaartekracht zal door zijn massa een kracht uitoefenen op de vloeistof daaronder. Om die reden neemt de waterdruk toe als een functie van de diepte.

Voor een vloeistofkolom geldt dat de druk op een bepaalde afstand van het oppervlak gelijk is aan de druk veroorzaakt door die vloeistofkolom en de druk van de atmosfeer boven die vloeistof. We spreken dan van de hydrostatische druk. In formule:

p = p0 + r.g.h

Waarin:

  • p  : hydrostatische druk (Pa)
  • p0 : atmosferische druk (Pa)
  • r : de dichtheid van de vloeistof (kg/m3)
  • g: de gravitatieconstant (9.8 m/s2)
  • h: diepte (m)

Deze formule kunnen we gebruiken om de theoretische resultaten met de praktische te vergelijken.

Het verschil tussen theorie en praktijk is verrassend klein, beter dan ik verwachte. Zo nauwkeurig kunnen we de diepte niet meten, daar zit altijd wel een fout van een paar mm in. Dat effect is dus te verwaarlozen.

De  metingen laten zien dat onder invloed van de zwaartekracht de hydrostatische druk toeneemt met de toenemende hoogte van de vloeistofkolom, dus met de vulhoogte van het vat. We kunnen ook waarnemen dat de hydrostatische druk niet afhangt van de vorm van het vat. De hydrostatische druk hangt ook niet af van de richting waarin de druk wordt gemeten alhoewel we dat niet duidelijk aangetoond hebben met deze experimenten.

Voor het medium water kan men de vuistregel hanteren dat een druk van 1 bar overeenkomt met een hoogte van de waterkolom van 10 m.

Opmerkingen:

  • Ik gebruik de moeren en ringen om de slang een beetje recht te laten hangen.
  • Het doet er niet echt toe of de slang recht hangt. Wat van belang is dat men meet vanaf het open eind van de buis.
  • Bij grotere dieptes kan een kleine hoeveelheid water de buis in kruipen als de lucht in de buis samengeperst wordt. In dat geval moet men de diepte meten vanaf het water oppervlak tot het waterniveau in de buis.
  • Hydrostatica staat voor de leer van het evenwicht an de vloeistoffen
  • De resultaten zijn samengevat in de exel file: resultaten.xlsx
  • De Coachlab 7 file: Hydrostatisch_20211121.cmr7
  • Specificaties druksensor:
    Pressure Range: 0 to 210 kPa 
    Accuracy: ±4 kPa
  • We hebben dit experiment met kraanwater uitgevoerd. Een vervolgexperiment zou kunnen zijn om dit experiment  met zout water uit te voeren. Dermate aangezout dat de dichtheid duidelijk boven die van kraanwater zit. De theorie zegt dat de drukverschillen groter zouden moeten worden dan die met water gemeten.

Literatuur:

  • J.A. Tijmensen, B. Taken; "Natuurkunde voor het MLO  1"; Heron Reeks; Bohn, Scheltema & Holkema; 1986; ISBN 9031307637;  p. 128-132.
  • Robert Gardner; "Experimenting with Water"; Dover; 1993; ISBN 0486434001; p. 73-78.
  • J. Cunningham, N. Herr; "Hands-On Physics Activities with Real-Life Applications: Easy-to-Use Labs and Demonstrations for Grades 8 - 12"; Jossey-Bas; 1994; ISBN-13: 978-0876288450; p. 238,239

Relevante websites:

Minder relevante websites:

Achtergrondinformatie:

De druk word gedefinieerd als kracht per oppervlakte-eenheid:

In formule: p = F/A

waarin:

  • p = druk (N/m2)
  • F  = kracht op A (N)
  • A = oppervlakte waarop F werkt (m2)

Voor N/m2 , de eenheid van druk, is de benaming pascal (Pa) ingevoerd. Er  geldt dus:

1 Pa is de druk die veroorzaakt wordt door de kracht van 1 N op een oppervlakte van 1 m2.