Experimenteren met een Texas Instruments TI-nspire rekenmachine en een temperatuursensor


|
Experimenteren met een Texas Instruments TI-nspire rekenmachine en een temperatuursensor |
 |

|
Datum: Maart 2022
Inleiding:
| Ik heb via Marktplaats een TI-Nspire CX met temperatuursensor gekocht en dan wil men er ook een experiment mee uitvoeren. |
Principe:
| De dubbelwandige calorimeter kan gebruikt worden om te bepalen of een reactie exotherm is. |
Materiaal:
|
|
 Temperatuur sensor |
|
Koffiekop calorimeter:
|
|
 |
Uitvoering:
| Bouw de opstelling op zoals weergegeven in nevenstaand schema en onderstaande foto. |
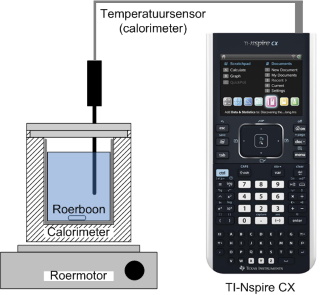 |
 |
|
|
|
Resultaten en discussie:
|
De chemische reactie die plaats vindt
in de calorimeter is: Mg(s) + 2H3O+ 2Cl- --> H2(g) + Mg2+ + 2Cl- + 2H2O |
|
| Experiment 1 | Experiment 2 |
|
Zoutzuuroplossing: 30.069 g Magnesium: 71 mg |
Zoutzuuroplossing: 51.7 g Magnesium: 104 mg |
|
Koppelen we de rekenmachine aan de computer dan kunnen we de meetresultaten op de computer inladen en analyseren m.b.v. de Texas Instruments software. |
|
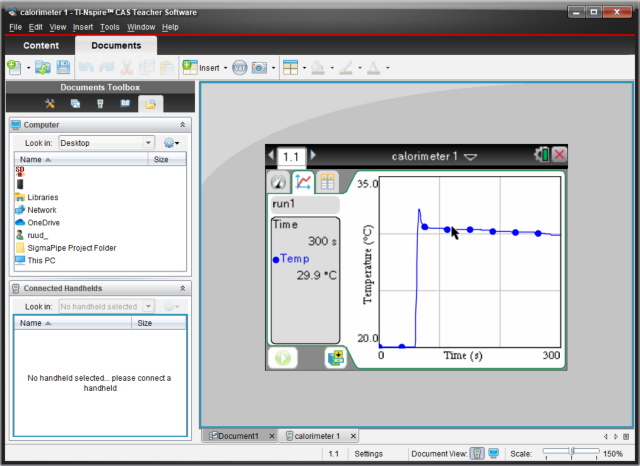 |
|
|
Binnen de software (of op de
rekenmachine zelf) kunnen we de data analyseren en de benodigde
temperaturen aflezen. |
|
|
Experiment 1: Minimum Temperatuur: 20.1 ░C Maximum Temperatuur: 32.1 ░C Na piekje: 30.6 ░C Temperatuurverschil: 12 ░C Temperatuurverschil na piekje : 10.5 ░C Dit piekje in de temperatuurgrafiek is eigenlijk iets dat we niet verwachten en suggereert eigenlijk dat de warmte in het begin niet goed verdeelt werd over de vloeistof. Het is daarom beter om de temperatuur direct na het piekje te gebruiken.
|
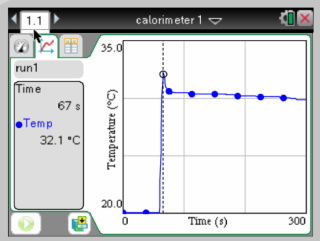 |
|
Experiment 2: Herhaling van het eerste experiment maar we hebben de zoutzuuroplossing wat verdund om er zeker van te zijn dat de temperatuurmeter voldoende ondergedompeld is. Minimum Temperatuur: 32.6 ░C Maximum Temperatuur: 22.7 ░C Temperatuurverschil: 9.9 ░C Dit tweede experiment laat zien dat het piekje inderdaad een afwijking was. |
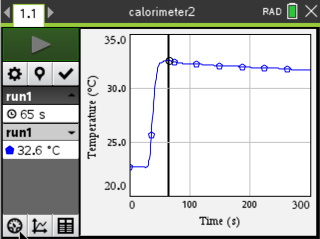 |
|
De temperatuurtoename laat zien dat deze reactie exotherm is. |
|
| Als
warmte toegevoegd wordt aan een vloeistof of een vaste stof dan
wordt deze warmte gebruikt om de interne energie van het system te
verhogen hetgeen we waarnemen als een temperatuursstijging. De
relatie tussen de geleverde warmte en de temperatuur wordt
weergegeven door:
Q = m.Cp.∆T Passen we dit toe op bovenstaand
experiment dan berekenen we: Relateren we dit terug naar de hoeveelheid toegevoegd Magnesium (71/1000/24.305 = 0.002921 mol) dan berekenen we voor deze reactie: 1319.73/1000/0.002921 = 451.807 kJ/mol Voor het tweede experiment
berekenen we: Gemiddeld: 475.9 kJ/mol
|
|
| Om dit getal nu te koppelen aan de theorie maken we gebruik van de Wet van Hess, schematisch weergegeven in onderstaand schema. | ||||||||||||
|
|
||||||||||||
|
Men heeft de enthalpieen van de elementen in hun meest stabiele vorm bij 1 atm en 298 K gelijk nul gesteld. Als een mol van een verbinding uit zijn elementen in de meest stabiele vorm onder deze standaardomstandigheden gevormd wordt, dan is de hierbij optredende reactie-enthalpie gelijk aan de enthalpie van de gevormde verbinding. De warmte die gevormd worden is het directe resultaat van de vormingswarmte (∆Hf) van het Magnesium chloride hetgeen we als bruto reactie als volgt kunnen schrijven: Mg(s)+2HCl(l)--> H2(g)+MgCl2(aq) De bindingen die verbroken worden zijn:
De bindingen die gevormd worden zijn:
|
||||||||||||
|
Relevante standaard bindingsenthalpieŰn
|
| Bij
benadering: ΔH0reactie= [ΔH0f (MgCl2(aq)) + ΔH0f (H2(g))] - [ΔH0f (Mg(s)) + 2ΔH0f (HCl(aq))] = [-796.9+0]-[0+2*(-167.2)] = -462.5 kJ/mol |
| Een negatieve vormingsenthalpie is per definitie, exotherm. |
Vergelijken we deze berekende waarde (-462.5 kJ/mol) met de gemeten waarde (-476 kJ/mol) dan hebben we een aardige overeenkomst. Een opmerking die we onmiddellijk maken is dat we niet gecorrigeerd hebben voor de warmtecapaciteit van de calorimeter. Voor dit type koffiekop calorimeter valt dat typisch in de range 50 - 500 J/░C. Zo te zien verwaarloosbaar voor dit type experimentele opstelling. |
Conclusie:
|
Opmerkingen:
|
Literatuur:
|
Relevante websites:
Minder relevante websites:
|
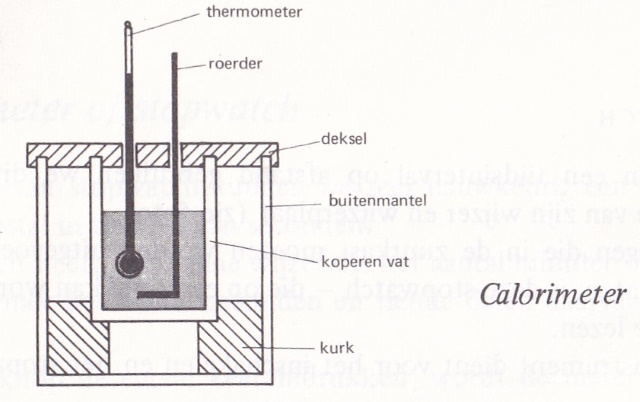
Achtergrondinformatie: Principe calorimeter Willen we iets te weten komen over de hoeveelheid warmte die vrijkomt bij of nodig is voor een proces, dan gebruiken we een calorimeter. Een calorimeter is een toestel waarbij de warmte-uitwisseling met de omgeving tot het uiterste wordt beperkt. Zo wordt er voor allerlei bepalingen (soortelijke warmte, verdampingswarmte, smeltwarmte, etc.) gebruik gemaakt van een calorimeter. In principe kan men reeds warmte meten mbv een metalen bakje met een dunne wand. Dit bakje wordt dan op een laagje plastic gezet. In het bakje worden een thermometer en een roerder geplaatst. Verder is het bakje met water gevuld. Door het water te roeren wordt ervoor gezorgd dat de temperatuur overal in het bakje gelijk is. Een laboratorium calorimeter lijkt erg veel op bovenstaande opstelling er zijn echter een paar belangrijke verschillen. Het belangrijkste onderdeel is een koperen bak. Deze bak is omgeven door een tweede bak, zodat er een isolerende luchtlaag ontstaat hetgeen resulteert in een minimum aan warmte-uitwisseling met de omgeving. Daarom is de binnenste bak een laag kurk geplaatst en is het geheel afgeschermd door een deksel van perspex, waardoor een thermometer en een roerder kunnen worden gestoken. De roerder heeft de vorm van een ring zodat bij het op en neer bewegen de vloeistof tot stroming wordt gebracht. Hierdoor vindt er een snelle en gelijkmatige warmteverdeling plaats. |
 |
|
Daar de calorimeter, de thermometer en de roerder, bij menging van twee stoffen van verschillende temperatuur, temperatuurveranderingen ondergaan , moet het aantal Joule dat de calorimeter met toebehoren, per graad temperatuurstijging opneemt (dit is de warmte capaciteit van de calorimeter) bepaald zijn. Bij het verrichten van metingen met de calorimeter moet er op toegezien worden dat de begin- en eindtemperatuur van de calorimeter zo worden gekozen, dat deze symmetrisch liggen t.o.v de. kamertemperatuur. Dit om eventuele warmte-afgifte aan en warmte-opname van de omgeving zoveel mogelijk aan elkaar gelijk te maken, waardoor de hierdoor optredende fout zo klein mogelijk wordt gehouden. De warmteafgifte of warmteopname q naar of van een massa m is gerelateerd aan de te temperatuursverandering DT volgens: q = Cp.m.DT waarbij Cp de specifieke warmte capaciteit van die massa is bij constante druk. Voor water: Cp = 4.18 J/(g.░C) |
|
Enkele standaard bindings enthalpieen |
|
|