Het afkoelingseffect van een ventilator
(CoachLab experiment)

Datum: Juni 2023

Inleiding:

Koelt een ventilator je nu echt af? Het voelt soms wel zo maar klopr dat?

Materiaal:

  • Computer met Coachlab software
  • CoachLab II
  • Temperatuursensor
  • Contact temperatuursensor
  • USB ventilator
  • Dikke reageerbuis
  • Water
  • Vloeipapier
  • Elastiekjes
  • Balans
  • Bekerglas
  • Reageerbuishouder


CMA CoachLab II


Temperatuur sensor


Contact temperatuursensor

Uitvoering:

  • Neem een vel vloeipapier en een glazen buis
  • Wikkel het vloeipapier om de glazen buis heen en zet het vast met elastiekjes
  • Plaats de contactthermometer tussen de glaswand en het papier
  • Plaats de buis in een houder en vul deze met water
  • Plaats de temperatuurmeter in het water
  • Configureer Coachlab (1 uur meten, 1 meting per 10 s)
  • Positioneer de ventilator op korte afstand van de buis
  • Start de meting en zet tegelijkertijd de ventilator aan
  • Bevochtig na ca. 20 minuten het papier met water
  • Herhaal de meting twee keer
  • Plaats een bekerglas op de balans en tarreer
  • Leeg de buis in het bekerglas en noteer hoeveel water in de buis zat
  • Weeg de lege buis met het droge papier er omheen gewikkeld
  • Bevochtig het papier en weeg opnieuw
  • Bereken hoeveel water is opgenomen door het vloeipapier
  • Exporteer vanuit CoachLab de resultaten als csv file en importeer deze in Excel voor verdere analyse

 

Resultaten:

Weegcijfers:
Water in buis: 41.929-7.491 = 34.44  g
Wateropname door vloeipapier = 33.953-30.400 = 3.55 g

Screenshot Coachlab na 3 experimenten:
 
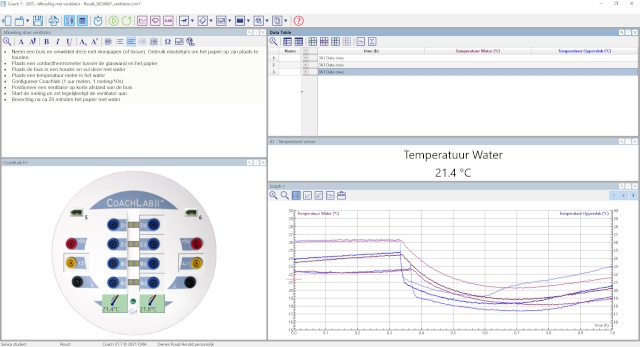De data is geëxporteerd naar Excel en samengevoegd in een grafiek.
Van elke grafiek is het minimum en het maximum bepaald en vervolgens het verschil berekend.

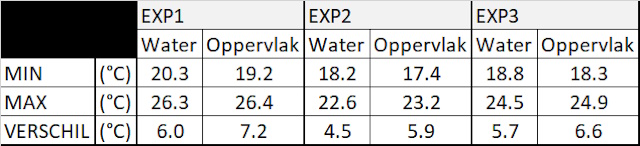Discussie:

We zien dat de ventilator  geen invloed heeft op de watertemperatuur als het papier droog is. Dat veranderd als we het papier gaan bevochtigen. Dan observeren we dat het vloeipapier zelf zeer snel afkoelt terwijl de afkoeling van het water na-ijlt.

Het eerste deel van dit experiment laat zien dat een ventilator op zich niet voor afkoeling zorgt, in tegenstelling tot wat in veel ventilator advertenties beweerd wordt. Alleen de lucht wordt in beweging gebracht.

Het tweede deel van dit experiment laat mooi het effect van natte kleren zien die jet laat drogen aan je lichaam als je in een briesje staat. De verdamping van het water zal ervoor zorgen dat je huidtemperatuur flink zal dalen. In dit experiment houden we echter geen rekening met het feit dat ons lichaam zelf warmte produceert en dus zijn best zal doen om de temperatuur van het lichaam constant te houden. Desalniettemin impliceert dit experiment dat je een sterke afkoeling van de huid zou kunnen verwachten. Dit deel van het experiment laat ook zien dat als je aan het zweten bent, en je zet dan een ventilator aan, dan kun je wel wat afkoeling verwachte.

De tweede vraag die we ons kunnen stellen is of we dit effect kunnen kwantificeren als we gebruik maken van de verdampingswarmte van water.

De warmteafgifte of warmteopname q naar of van een massa m is gerelateerd aan de te temperatuursverandering ΔT volgens: q = Cp.m.ΔT  waarbij Cp de specifieke warmte capaciteit van die massa is bij constante druk. Voor water: Cp = 4.18 J/(g.°C) 

De verdampingswarmte van water: 2256 kJ/kg = 2556 J/g

Het vloeipapier heeft 3.55 g water opgenomen. Om dit water te verdampen heeft men nodig aan energie:
3.55 * 2556 = 9073.8 J

In de reageerbuis zit 34.44 g water.

Met q = Cp.m.ΔT krijgen we:
9073.8 = 4.18 * 34.4 * ΔT Þ ΔT = 63 °C

Dat is dus een veel groter temperatuurdaling dan we daadwerkelijk waarnemen. Nu hebben we het glas van de reageerbuis niet meegenomen in deze berekening maar glas is een goede geleider, daar verklaart men het verschil niet mee.

Het systeem is dus complexer dan we in eerste instantie dachten. We hebben niet alleen maar met warmteuitwisseling tussen twee lichamen te maken maar ook met het effect van een bewegende luchtstroom. Reden om gedetailleerder naar warmtetransport te kijken.

Als twee lichamen met verschillende temperatuur met elkaar in contact komen zal er warmteoverdracht van het lichaam met de hogere temperatuur naar het lichaam met de lagere temperatuur plaatsvinden. De overdacht van warmte kan op drie manieren plaatsvinden:

  • Convectie of meevoering van warmte: de warmte wordt overgebracht door bewegende materie
  • Conductie of geleiding: de warmte wordt overgebracht d.m.v. materie die zich niet verplaatst
  • Radiatie of straling: de warmte wordt overgebracht zonder bemiddeling van materie.

In de praktijk vindt de overdracht van warmte meestal plaats door een combinatie van deze mechanismen.

Convectie is alleen mogelijk in vloeistoffen en gassen, omdat nodig is dat de verschillende delen van de stof t.o.v. elkaar kunnen bewegen. Verwarmt men de onderste lagen van een vloeistofkolom, dan wordt de dichtheid van de vloeistof ter plaatse kleiner. Daardoor stijgt de verwarmde vloeistof op en beweegt de vloeistof uit de bovenste, koudere lagen zich naar beneden. Deze vloeistof wordt dan daar ook weer verwarmd en stijgt op, zodat een circulatie van vloeistof ontstaat.

Straling levert meestal maar een kleine bijdrage en kan waarschijnlijk verwaarloosd worden.

Het systeem waar we in dit experiment naar kijken wordt gedomineerd door convectie, meer specifiek geforceerde convectie. M.b.v. een ventilator brengen we een stroom (onverzadigde) lucht in direct contact met een oppervlakte. Convectie wordt beschreven met de afkoelingswet van Newton. Volgens Newton's wet van afkoeling geldt voor een voorwerp dat afkoelt o.i.v. geforceerde convectie (luchtstromingen) dat de snelheid van afkoeling evenredig is met het verschil in temperatuur tussen het voorwerp en zijn omgeving (zie Achtergrondinformatie).

De tweede factor die ook een rol speelt is dat we ons oppervlak nat gemaakt hebben. We krijgen dan te maken met adiabatische koeling.

Bij adiabatische koeling wordt een stroom onverzadigde lucht in direct contact gebracht met een nat oppervlak. De grenslaag rond het natte oppervlak is op natuurlijke wijze verzadigd met waterdamp. Omdat onverzadigde lucht langs de grenslaag stroomt, zal waterdamp zich in de luchtstroom verspreiden, aangedreven door een verschil in dampconcentratie. Het waterdampgehalte in de grenslaag wordt dan door de adiabatische verdamping van het water weer in de natuurlijke verzadigde toestand gebracht. De benodigde latente warmte voor de faseverandering van het water wordt uit de voelbare warmte van de luchtstroom gehaald, wat resulteert in een lagere luchttemperatuur.

De laagst mogelijke temperatuur die kan worden bereikt is de natte-boltemperatuur van de lucht, maar is in de praktijk iets hoger vanwege een beperkt rendement. Het verzadigingsrendement of nattebolrendement wordt gedefinieerd als de verhouding tussen de daadwerkelijk bereikte temperatuurdaling en de maximaal mogelijke temperatuurdaling.

Wat we in dit experiment gebouwd hebben is iets dat op een koeltoren lijkt, met een groot verschil nl dat het medium dat we afkoelen (water) stationair is maar ook dat het water dat we toevoegen aan het filtreerpapier begrensd is, hetgeen het een batchproces maakt. De opstelling is schematisch weergegeven in onderstaande schets.
 
 
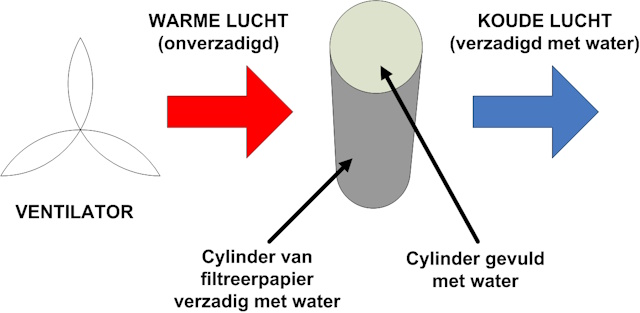In de praktijk kan men waarnemen dat de uitgaande lucht dan tussen de 60 en 90% van de natteboltemperatuur kan worden afgekoeld, afhankelijk van de effectiviteit van de opstelling. De aangevoerde lucht wordt 10 tot 15°C afgekoeld. Deze getallen zijn van toepassing op een meer gesloten systeem waarbij men het koelmedium (hier filtreerpapier) continue bevochtigd.

In dit experiment meten wij echter niet de temperatuur van de lucht maar van het oppervlak en de kern van de cylinder en daar meten we een temperatuurdaling van maximaal 5 to 6 °C. Als men dan in beschouwing neemt dat het enige tijd duurt om op die laagste temperatuur uit te komen en dat op dat punt al een groot deel van het water verdampt is, dan is het logisch dat men niet de temperatuurdaling kan halen die vermeld wordt. Ons systeem komt pas in evenwicht met de omgeving als al het water verdampt is. Het koelvermogen zal (waarschijnlijk exponentieel) als functie van de hoeveelheid verdampt water afnemen. Zo bezien is een temperatuurdaling van 5 a 6 °C  helemaal niet zo'n slecht resultaat.

Op dit punt aangekomen gaat men zich ook afvragen of men zulk een systeem kan modelleren. Het antwoord is dan waarschijnlijk: alleen bij benadering. Gezien het aantal variabelen waar we hier mee te maken hebben zou je waarschijnlijk ook een beroep moeten doen op Computational Fluid Dynamics (CFD) berekeningen. Maar zelfs voor CFD berekeningen zal ik als input meer parameters moeten bepalen, waaronder bv de luchtflow. 

Al met al betekent dat een aanpassing van de meetopstelling. Hier stel ik me momenteel het volgende bij voor.
Neem een PVC buis met een flinke diameter en ca 1 m lengte, In het midden van de buis maken we een opening waarin we de buis met water en filtreerpapier kunnen plaatsen. Aan de ingang van de buis plaatsen we de ventilator. We plaatsen extra temperatuurmeters upstream en downstream de watercilinder om de luchttemperatuur voor en na koeling te kunnen meten. De luchtsnelheid kunnen we meten met een Anemometer aan het einde van de buis en aangezien we de diameter van de buis kennen kunnen we m.b.v. deze meting de luchtflow berekenen. Het noteren van de luchtdruk en temperatuur van de omgeving maakt het mogelijk om de natteboltemperatuur te bepalen. In zulk een opstelling zou men ook een meting kunnen uitvoeren waarbij men het filtreerpapier continue bevochtigd. De cilinder gevuld met water zal mogelijk een dempende werking hebben op de verdamping van het water in het filtreerpapier, men kan dus ook een experiment met een lege cilinder uitvoeren om te kijken welke invloed het water heeft.

Al met al was dit typisch zo'n experiment dat er in eerste instantie eenvoudig uit ziet (en men dus denkt dat doen we wel even) maar dat dan op basis van de meetresultaten onmiddellijk laat zien dat het systeem veel complexer is.

Conclusies:

  • Een ventilator verplaast alleen maar lucht en koelt een oppervlak niet af.
  • Ventilatie gecombineerd met waterverdamping zorgt wel voor afkoeling.

Opmerkingen:

  • In plaats van vloeipapier kan men ook tissues gebruiken
  • Ik heb een voorkeur voor het analyseren van data in Excel. Men kan echter ook data-analyse binnen CoachLab zelf uitvoeren.

Literatuur:

  • R. Frost; "Data logging in Practice"; IT in Science; ISBN 0952025744; p 123.

  • J.M.M. Smith, E. Stammers; "Fysische Transportverschijnselen I"; Delftsche Uitgevers Maatschappij; 1973; p. 77-130.

  • B. van Buuren, J.H. Smit; "Natuurkunde voor de HTS"; 6de druk; Educaboek; 1967; ISBN 9011008960; p. 152-165.

Relevante websites:

Minder relevante websites:

Achtergrondinformatie:

Volgens Newton's wet van afkoeling geldt voor een voorwerp dat afkoelt o.i.v. geforceerde convectie (luchtstromingen) dat de snelheid van afkoeling evenredig is met het verschil in temperatuur tussen het voorwerp en zijn omgeving. Aangezien het temperatuurverschil evenredig is met de verandering in warmte:


waarin m de massa van het voorwerp is en Cp de warmtecapaciteit, kunnen we schrijven:

waarin dT/dt de afgeleide van de temperatuur in de tijd is, Ts de omgevingstemperatuur en K een evenredigheidsconstante. Deze vergelijking kunnen we integreren waarbij we stellen dat op het tijdstip t=0 de temperatuur van het voorwerp T0 is.

Voor de T van het voorwerp op tijdstip t geldt dus:
 

09/07/2023