Brownse beweging


|
Brownse beweging |

|

|
Datum: December 2010
Principe:
Botsingen van moleculen zichtbaar maken onder de microscoop.
Materiaal:
|
|
|
|
|
 |
|
Experimentele opstelling:
|
|
 |
Uitvoering en resultaten:
|
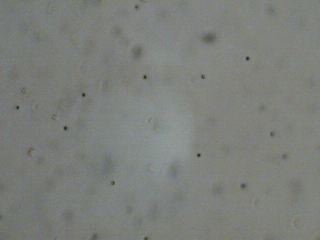
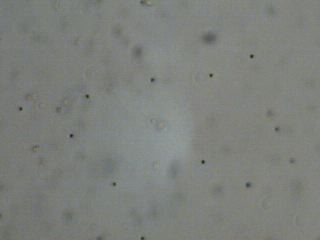
Het resultaat is weergegeven in nevenstaand
filmpje en onderstaande foto's.
In de foto's kan men zien dat de zwarte puntje van plaats zijn veranderd. Vaak zal men toestemming moeten verlenen om het filmpje te laten spelen |
YouTube link: Brownian Motion |
 |
 |
Discussie en conclusie:
|
In 1827 werd door de Engelse plantkundige
Robert Brown ontdekt dat van stuifmeel afkomstige deeltjes, gesuspendeerd in
water, een willekeurige trillende beweging vertoonden als deze onder een
microscoop bekeken werden. Later bleek dat kleine vaste deeltjes in een vloeistof
steeds dit verschijnsel vertonen.
In 1905 poneerde o.a. Albert Einstein de theorie die de Brownse beweging kon verklaring. Een vloeistof is opgebouwd uit moleculen, deze moleculen botsen voortduren met de suspensie deeltjes resulterende in een willekeurige beweging van die deeltjes. |
|
|
Op basis van Einstein's publicatie begon de
Franse fysicus Jean Perrin met het verzamelen van experimentele gegevens die
Einstein's theorie kon bewijzen. |
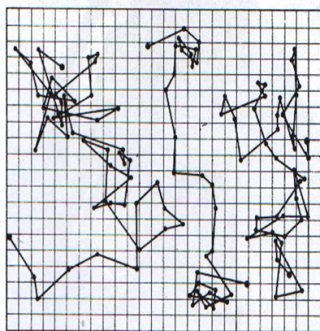 |
| Op basis van de gemiddelde kwadraten verplaatsingsvergelijking die door Einstein afgeleid was kon Perrin aantonen dat Einstein's theorie correct was. Op deze manier kan hij ook Avogrado's constante nauwkeurig bepalen. Robert Brown's brownse beweging, de publicatie van Albert Einstein en de experimenten van Jean Perrin tezamen worden beschouwd als het eerste onweerlegbare bewijs voor het bestaan van moleculen. | |
|
Brownse beweging wordt dus verklaard
door de botsingen van de vloeistofmoleculen tegen een gesuspendeerd deeltje.
Het is hierbij van belang zich te realiseren dat de beweging niet
veroorzaakt wordt door de botsing van slechts een vloeistofmolecuul met het
deeltje. Het massaverschil tussen molecuul en deeltje is te groot zodat van
een directe stoot niets te merken is. Tegen het deeltje botsen van alle
zijden de moleculen van de vloeistof en gemiddeld genomen zal het aantal
botsingen van alle kanten gelijk zijn. Gedurende een korte tijd kan het
echter voorkomen, dat het aantal botsingen aan een kant groter is dan aan de
andere kant, omdat de botsende moleculen door het toeval verdeeld zijn over
het oppervlak van het deeltje, zodat ook toevallige afwijkingen van het
gemiddelde mogelijk zijn. Het resultaat van deze "fluctuatie" is dan dat het
deeltje zich in een richting beweegt gedurende die korte tijd. Een ogenblik
later zal het deeltje zich weer in een andere richting verplaatsen met als
resultaat een zigzag beweging door de vloeistof. Onder de microscoop kunnen
we alleen de grotere verplaatsingen waarnemen. Volgens de kinetische
gastheorie kunnen we het verschijnsel ook zo interpreteren, dat het deeltje
deelneemt aan de warmtebeweging van de vloeitstofmoleculen en evenals deze
een gemiddelde kinetische energie 3/2kT heet (k = constante van Boltzmann, T
is temperatuur in K). Ten gevolge hiervan verplaatst het deeltje zich door
de vloeistof. Einstein berekende dat het kwadraat van de verplaatsing (Dx)
gedurende een tijd (t)
gelijk is aan:
Dit kwadraat van de verplaatsing neemt toe naarmate de temperatuur groter wordt. De viscositeit en de deeltjesstraal worden in de vergelijking geïntroduceerd omdat de gemiddelde wrijvingskracht die het deeltje bij het verplaatsen door de vloeistof ondervindt, volgens de wet van Stokes gelijk is aan 6.P.h.r.v, waarin v de snelheid van het deeltje is. Hoe groter de wrijvingskracht des te kleiner de verplaatsing van het deeltje in de vloeistof. De experimenten van Perrin hebben bovenstaande formule volledig bevestigd. Uit de metingen kan men vervolgens de constante van Boltzmann bepalen en die vervolgens weer gebruiken om het getal van Avogrado te bepalen: N = R/k (R = gasconstante) |
|
Literatuur:
|
|
Relevante websites: |
Opmerkingen:
|
Achtergrondinformatie:
| Robert Brown (Geboren in Montrose op 21 december 1773 - Gestorven in Londen op 10 juni 1858) was een Schotse botanicus. Hij studeerde medicijnen en nam in 1795 dienst in het Britse leger. Hij wordt algemeen beschouwd als de leidende Britse Botanicus betreffende Australische planten gedurende de eerste helft van de 19de eeuw. Hij wordt beschouwd als de ontdekker van de celkern die hij ontdekte toen hij orchidee cellen aan het bestuderen was onder de microscoop. Hij staat echter vooral bekend als de ontdekker van de naar hem vernoemde Brownse beweging. De grillige en onvoorspelbare beweging van stuifmeelkorrels die men door een microscoop waarneemt. |
|
30/12/2010