LR Inductie

Datum: Juni 2011

Principe:

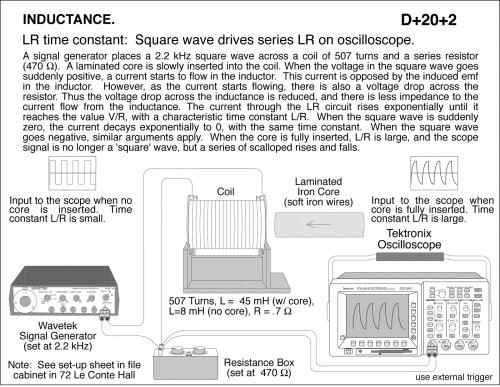
Inductie bestuderen met een oscilloscoop.

Materiaal:

Uitvoering:

  • Bouw de schakeling op zoals hiernaast schematisch is weergegeven.
  • Selecteer het blok signaal in op de functiegenerator en stel een frequentie van ca. 2.2 kHz in.
  • Als de kern in de spoel zit haal deze er dan uit.
  • Stel de uitlezing in op een spanning van 0.3 V.
  • Stel de variabele weerstand dusdanig in dat een maximale uitlezing mogelijk is.
  • Sla de meetdata op.
  • Stop de kern langzaam in de spoel en meet opnieuw.
  • Sla de meetdata op.
  • Analyseer de data.


 

Resultaat:

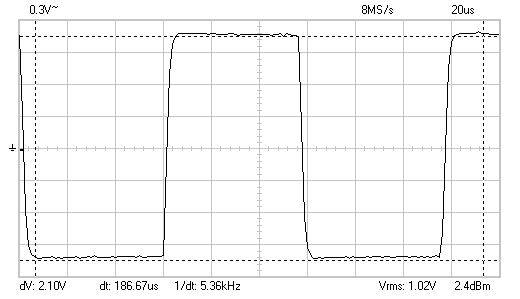
De meetresultaten zijn weergegeven in  onderstaande grafieken.
zonder magneetkern
met magneetkern


 

Discussie en conclusie:

Als we de kern langzaam in de spoel stoppen zie we dat als de spanning positief wordt er een stroom gaat lopen door de spoel. Deze stroom is tegengesteld aan het geïnduceerde emf in de spoel. Als de stroom begint te lopen is er echter ook een spanningsval over de weerstand. De spanningsval over de weerstand over de inductor is gereduceerd en er is minder impedantie naar de stroom vanuit de spoel. De stroom door het LR circuit gaat exponentieel omhoog totdat het de waarde V/R bereikt met een karakteristiek tijdsconstante van L/R. Als de blokgolf plotseling naar 0 gaat zal de stroom exponentieel afnemen met dezelfde tijdsconstante. Als de blokspanning negatief wordt kan men dezelfde redenatie volgen. Als de kern volledig in de spoel zit is L/R groot en laat de scoop niet langer een blokgolf zien maar een serie van golfvormen. Dat is in bovenstaan plaatje niet volledig gelukt maar het begin daarvan is waarneembaar.
Dit was een experimentje dat ik uitgevoerd heb om het effect te zien. Later wil ik dit experiment nog eens herhalen, met beter gedefinieerde spoelen, en dan ook dit experiment theoretisch beter uitwerken.

Literatuur:

Relevante websites:

Minder relevante websites:

Opmerkingen:

  • De handleiding van de experimenteerdoos is niet duidelijk over het aantal windingen in de spoel. Mogelijk zijn het er 550.

Achtergrondinformatie:

Indien we weerstanden, spoelen en condensatoren of combinaties daarvan op een sinusvormige spanning aansluiten vloeit er een sinusvormige stroom met in het algemeen een willekeurige faseverschuiving.

De "weerstand" die deze schakeling voor de sinusvormige spanning heeft wordt de impedantie (Z) genoemd. In formule analoog aan de wet van Ohm: Z = Umax/Imax

Indien de faseverschuiving tussen spanning en stroom 90° bedraagt spreken we van de reactantie (X) van een schakeling.

Zijn de spanning en de stroom in fase dan zegt men dat de schakeling zich Ohms gedraagt.
 
Als we een spoel via een weerstand op een spanningsbron aansluiten gaat er een stroom vloeien. De spoel gaat zich opladen doordat er een magnetisch veld om de spoel heen gevormd wordt. Dit opladen kost tijd nodig en als we de oplading grafisch uitzetten zien we een oplaadkromme.
Een spoel verzet zich ook tegen een verandering in de stroom men kan daarom een spoel beschouwen als een wisselstroomweerstand. De mate waarin een spoel zich verzet tegen stroomverandering noemt men zelfinductie.
Zoals reeds vermeld bouwt een spoel een magnetisch veld op als er eens stroom door de spoel heenstroomt. Onderbreken we de stroom dan zal de spoel de opgeslagen energie weer afstaan in de vorm van elektrische stroom. Als men dit plotseling doet  door de schakeling te verbreken kan de energie niet afgestaan worden en kan de spanning binnen de spoel tot een dusdanig hoge waarde stijgen dat er vonken ontstaan.

 
Samengevat:

Een stroomverandering binnen in een spoel wekt een zodanige EMK op dat deze de toename van de stroom tegenwerkt.

                                       (Henry:  H = V.s/A)

Anders geformuleerd:
Met een verandering van de stroomsterkte dI/dt in een geleider gaat een verandering  v/d magnetische flux gepaard. Deze induceert de EMK van de zelfinductie E.

Energie-inhoud van een spoel:

dq tegen de EMK in bewegen

Arbeid dan:

De totale arbeid om de stroom van 0 naar i te laten gaan:

 

Wisselstroom

Bij draaiing van een spoel in een magneetveld ω is de magnetische flux door de spoel afhankelijk van de tijd.

Als:

Dan is:

Dit is echter afhankelijk van het gekozen nulpunt en kan ook zijn:

Met f = 1/T en ω=2.p.f krijgen we ω=2.π/T

Hierin is ω de cirkelfrequentie, T de periode en f de frequentie

Volgens:

Geldt voor de EMK à E:

E = N.ω.φ0.sinω0.t 

Of als

E0 = N.ω.φ0

Dan E = E0.sin ω.t

Afhankelijk van het gekozen nulpunt kan dat dus ook zijn:

V = E = Vmax cos ωt

Weerstand

V = Vmax cos ωt       en  V = i . R  -->
                                      
i = Vmax / R . cos ωt       
imax = Vmax / R

 Spoel

Wisselstroomkring met inductieve belasting L

 
VL + V = 0

V = Vmax cos ωt            à       

De stroom loopt 90 ° na op de spanning.

ωL is de inductieve reactantie (wisselstroomweerstand).

Voor een spoel geldt : XL = ωL = 2.p.f.L

 

 

26/05/2017