De Lego Mindstorms RCX slinger

Datum: Februari 2010

Inleiding:

Jaren geleden ben ik ooit eens met een Lego project bezig geweest om een geinverteerde slinger te bouwen. Daar ben ik halverwege mee gestopt maar laatst realiseerde ik me dat de behaalde resultaten een uitstekend slinger, data logging en data analyse experiment beschrijven.

Principe:

Een slingerexperiment uitvoeren met de Lego Mindstorms RCX.

Materiaal:

  • Lego Mindstorms RCX
  • Rotatiesensor
  • 2 motoren
  • (Lego snelheidsmeter)
  • 10 kOhm weerstand
  • Lego bouwonderdelen zoals geleverd bij de Mindstorms kits.
  • Bricx Command Center (software voor aansturing RCX die het mogelijk maakt om NQC programma's te schrijven).
  • Computer met Excel
     


rotatiesensor              motor

Experimentele opstelling:

In eerste instantie heb ik de opstelling gebouw zoals in nevenstaande foto's is weergegeven.
De lego snelheidsmeter is niet echt noodzakelijk maar biedt de mogelijkheid om de gemeten snelheidswaardes te verifiëren.
Op zich is er geen Lego sensor die het mogelijk maakt om de snelheid te meten. Michael Gasperi heeft op p. 244 beschreven hoe we een motor kunnen gebruiken als snelheidssensor. Om de RCX sensor poort te beschermen is het echter noodzakelijk om minimaal een 10 kOhm weerstand in de sensorkabel op te nemen zoals weergeven in de onderstaande foto.  
De opstelling (exclusief snelheidsmeter) is ook beschikbaar als LDRAW file, die een meer gedetailleerde componentenlijst bevat: pendulum.ldr


 
Zoals hierboven getoond heb ik het experiment zoals het op deze pagina beschreven wordt uiteindelijk niet uitgevoerd. Hier wil ik alleen maar de slinger karakteristieken meten, ik heb dus geen motor nodig om de slinger aan te sturen (op te kunnen slingeren), ik heb slechts een motor nodig om de snelheid te meten. De uiteindelijke meetopstelling is dan zoals weergegeven op onderstaande foto.
De linkermotor wordt gebruikt als snelheidssensor en is ook gekoppeld aan de rotatiesensor. De weerstand die in het circuit is opgenomen is ook duidelijk te zien.
Een gelijkstroommotor in een open circuit produceert een voltage dat evenredig is met de hoeksnelheid. 

Door een van de twee draden in de LEGO connector door te knippen en er een weerstand in op te nemen beschermen we de sensoringang.

Het signaal dat een dergelijke versnellingssensor produceert bevat veel ruis. Ontruis het signaal door gebruik te maken van een filter.

Uitvoering en resultaten:

In nevenstaande filmpje is een experiment in uitvoering te zien.

De natuurkunde verteld ons dat een slinger een stabiele positie heeft waarbij de potentiële energie minimaal is. Dit is uiteraard de positie waarbij de massa naar beneden hangt. De lengte van deze slinger is 32 cm. Indien de slinger zich zuiver mathematisch zou gedragen zou deze een oscillatieperiode hebben van:

  

YouTube link: Lego Pendulum

De massa is echter niet regelmatig gedistribueerd. Om de gereduceerde lengte te bepalen moet men daarom metingen verrichten om de hoeksnelheid te bepalen.

Het experiment dat we uitvoeren is een gewone slingerbeweging waarbij we de slinger optillen en weer loslaten. De sensoren registreren dan verschillende waardes die geïnterpreteerd worden om de hoeksnelheid te kunnen berekenen. Voor het registreren van de sensorwaardes maken we gebruik van een klein NQC datalogging programma.
  
// measuring angle and speed of a pendulum
// timer functions in 10 ms intervals
# define DATALOG_SIZE 2000
task main()
{
 SetSensorType (SENSOR_1, SENSOR_TYPE_ROTATION);
 SetSensorType (SENSOR_3, SENSOR_TYPE_TOUCH);
 SetSensorMode(SENSOR_1, SENSOR_MODE_ROTATION); // rotation
 SetSensorMode(SENSOR_2, SENSOR_MODE_RAW );     // raw value
 SelectDisplay(1);                  // raw value on RCX display
 CreateDatalog(DATALOG_SIZE);
  ClearTimer(0);                    // Set de timer to 0
  

 int i=0;
 while (i < DATALOG_SIZE)
 {
       AddToDatalog(i);                   // add counter to datalog
       AddToDatalog(FastTimer(0));  // add time to datalog
       AddToDatalog(SENSOR_1);      // add sensor value to datalog
       AddToDatalog(SENSOR_2);      // add sensor value to datalog
       i++;
 }
 PlaySound(3);                      // tell us its over
}


De ruwe data wordt opgeslagen in een tekst file. Deze lezen we vervolgens in in Excel en converteren deze m.b.v. een eenvoudige macro naar een handzamer formaat.
 
Sub ProcessData()
'Program to convert LEGO datalog values to a more operatable form.
' @ 16/10/2005 by Ruud.Herold

'Notes:
'index = row, column

'Define some variables
Dim CounterData As Integer 'counter in processed data sheet
Dim CounterRaw As Integer 'counter in Raw data sheet

'Initialize variables
CounterRaw = 1
CounterData = 2

'Start of program
While Worksheets("rawdata").Cells(CounterRaw, 1).Value <> ""
If Worksheets("rawdata").Cells(CounterRaw, 1).Value <> "" Then
Worksheets("data").Cells(CounterData, 1).Value = Worksheets("rawdata").Cells(CounterRaw, 2).Value
Worksheets("data").Cells(CounterData, 2).Value = Worksheets("rawdata").Cells(CounterRaw + 1, 2).Value
Worksheets("data").Cells(CounterData, 3).Value = Worksheets("rawdata").Cells(CounterRaw + 2, 2).Value
Worksheets("data").Cells(CounterData, 4).Value = Worksheets("rawdata").Cells(CounterRaw + 3, 2).Value
End If
CounterRaw = CounterRaw + 4
CounterData = CounterData + 1
Wend

End Sub
 
De data die we mbv dit programma verzameld hebben analyseren we vervolgens verder in Excel (datalog.xls).

De eerste sensordata die we analyseren is de data van de rotatiesensor. Het was even puzzelen hoe de meetdata geïnterpreteerd moest worden.
Een rotatiesensor telt/leest 16 posities per rotatie van de as met een maximale resolutie van 500 rpm. In de firmware is het gekalibreerd om of hoeken of 1/16'de rotaties te meten. In dit geval meten we de rotaties.

De rotatiesensor is echter aan de slinger gekoppeld via tandwielen. Op de sensor zelf zit een 8 punts tandwiel en op de as van de motor een met 40 punten. De overdrachtsverhouding is dus 1 op 5.

Een volledige rotatie van het kleine tandwiel is 16 counts van de rotatiesensor. Ik draai de slinger eerst helemaal op naar de bovenste stand,  en laat hem dan los. Van de hoogste naar de laagste stand komt overeen met een afstand van 180°, daarna klimt de slinger weer omhoog. 180° komt overeen met 20 tandjes. M.a.w. 20/8 rotaties = 20/8 * 16 counts = 40 counts. Op 40 counts zou dan het diepste punt moeten liggen waarom heen de slinger op en neer beweegt. Kijken we naar de ruwe meetdata dan klopt dat aardig. De vertaalslag naar graden maken we als volgt: 180°/40 = 4.5° per count. Door nu te stellen dat het laagste punt op 0° ligt bereken we de positie t.o.v. dat punt met de volgende formule: meetwaarde * 4.5 - 180. 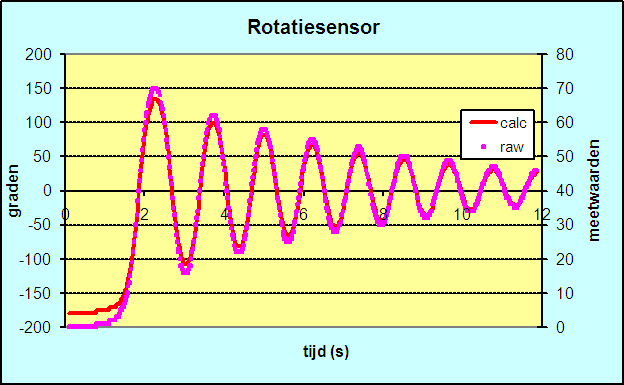De resultaten zijn weergegeven in onderstaande grafiek.
 

Noteren we nu de nulpunten uit de opgeschoonde grafiek dan kunnen we van daaruit de trillingstijd berekenen. Nemen we dan de laatste waardes uit de serie, waar de hoek dus relatief klein is, dan berekenen we een trillingstijd van 1.11 s. Een waarde die zeer dicht bij de theoretische van 1.135 s ligt.
 
Een Lego  motor is een DC type motor waarbij men normaliter een spanning over heen zet waarna de as gaat roteren. Dit proces kan men ook omdraaien, als de as draait wordt er een spanning gegenereerd. De te sneller de as draait des te meer spanning gegenereerd wordt. De polariteit van de spanning wordt bepaald door de richting waarin de as draait, met de klok mee of tegen de klok in. We nemen alleen een weerstand in de schakeling op om de sensor poort te beschermen. Deze weerstand creëert een aarde als de tachometer niet draait.

De tachometer geeft vrij nauwkeurig de hoeksnelheid van de slinger weer.  Als we een eerste blik op de meetdata werpen ziet een en ander er redelijk netjes uit.
 


Indien we echter een blik werpen op de 1ste afgeleide van het sensorsignaal dan kunnen we onderstaande grafiek produceren.
 


In de 1ste afgeleide zien we een ontzetten ruizig signaal, pieken die daar niet thuishoren. Deze worden veroorzaakt door hoog frequente variaties in de spoel van de motor die ontstaan t.g.v. het sampling proces. Deze variaties kunnen we er uit filteren m.b.v. een zgn infinite response filter:

                           Gemiddelde = (Lopend Gemiddelde + meetwaarde + 511)/3

Hierin is 511 onze eerste meetwaarde.
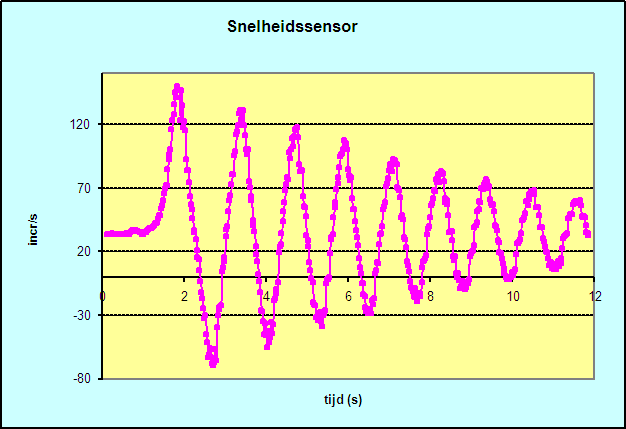
Het resultaat is weergegeven in onderstaande grafiek.
 


Voor de conversie naar rotatie-sensor incrementen per seconde gebruiken we de vergelijking:


 

Ook nu kunnen we de ""nulpunten"gebruiken om de trillingstijd berekenen. Wederom vinden we een waarde van 1.11 s.
 
De berekening van de trillingstijden kunnen we ook weer grafisch weergeven.
In de grafiek kunnen we dan waarnemen dat bij kleinere hoeken de triliingstijd zich min of meer stabiliseert.
 

 
We kunnen ook de dempingsfactor berekenen door van bovenstaande grafiek steeds de absolute waarde te berekenen hetgeen resulteert in onderstaande grafiek.
 

De dempingsfactor bereken je dan door opeenvolgende de ratio van de toppen te nemen en deze vervolgens te middelen. Op deze manier berekenen we een dempingsfactor van 1.1. Hoe lager deze dempingsfactor des te  minder weerstand de slinger ondervindt.
 
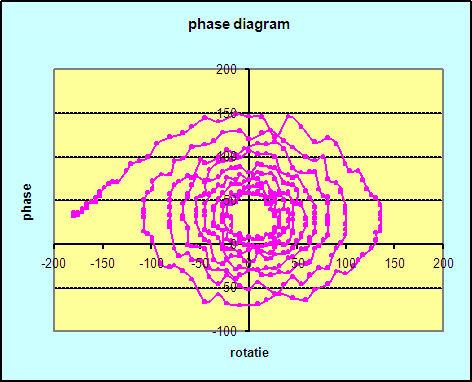
Als we de wiskunde bestuderen die betrekking heeft op de slinger dan is het noodzakelijk om te onderkennen dat we bij grote hoeken, waar we de vereenvoudiging sin(A) = A niet meer kunnen toepassen, we te maken hebben met een niet-lineair systeem. Bij de niet-lineaire systemen is er vaak geen analytische oplossing mogelijk van de differentiaalvergelijking die het systeem beschrijft.

Een fase ruimte is een verzameling van mogelijke toestanden van een analytisch systeem. Een fase ruimte kan eindig zijn (bv bij het opgooien van een muntje hebben we maar twee toetstanden nl kop en munt), telbaar eindig (bv. toestandsvariabelen zijn integers) en ontelbaar oneindig (bv toestandsvariabelen zijn complex). Impliciet wordt hierbij aangenomen dat een bepaalde toestand in de fase ruimte het systeem volledig beschrijft, alles dat we over het systeem moeten weten om de nabije toekomst te kunnen beschrijven is aanwezig. De fase ruimte van een slinger is 2-dimensionaal en bevat de positie (hoek) en snelheid. Volgens Newton kan door het specificeren van deze twee variabelen de daaropvolgende beweging van de slinger beschreven worden.

Het fasediagram dat we gemeten hebben wordt weergegeven in onderstaande figuur.
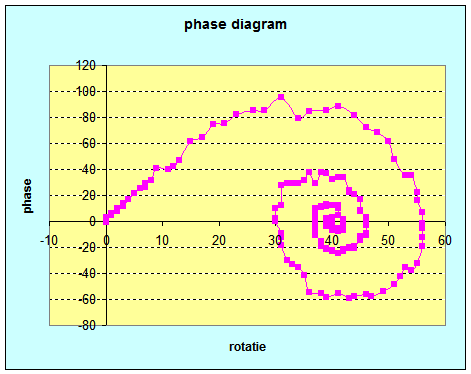
In bovenstaande experiment was de slinger op het einde van de meetperiode nog in beweging. Onderstaande experiment geeft het fase diagram weer van een experiment waarbij een aansturingsmotor in het systeem was opgenomen zoals oorspronkelijk gepland.

Conclusies:

  • De gemeten trillingstijd van deze slinger is 1.11 s, een waarde die zeer dicht bij de theoretische waarde van 1.135 s ligt.
  • De gemeten dempingsfactor in dit systeem is 1.1.

Literatuur:

  • Dave Baum (Editor), Michael Gasperi, Ralph Hempel, Luis Villa, David Baum; 'Extreme Mindstorms: an Advanced Guide to Lego Mindstorms' ; Apress; 1st Ed.; 2000; ISBN 1893115844; p. 244.
  • K.J. Astrom, K. Furuta; 'Swinging up a pendulum by energy control'; Automatica; 2000 36, p. 287-295.
  • Neil A. Downie; 'Vacuum bazookas, electric rainbow yelly and 27 other saturday science projects; Princeton; 2001; ISBN 0691009864; p. 21-27.
  • B. van Buuren, J.H. Smitt; "Natuurkunde voor de h.t.s."; Stam; 6de druk; 1967; ISBN 9011008960; p.246,247.
  • P.J. Gawthrop, E. McGookin; 'A LEGO-Based Control Experiment'; IEEE Control Systems Magazine; October 2004; p. 43-56.
  • R.A. Nelson, M. G. Olsson; 'The pendulum - Rich physics from a simple system'; American Journal of Physics; 54 2 1986; p. 112-121.
  • E. I. Butikov; 'The Rigid Pendulum - an Antique but Evergreen Physical Model'; European Journal of Physics; 20 6 1999; p. 429-441.

Relevante websites:

Minder relevante websites:

Opmerkingen:

  • Engelse Google zoektermen: pendulum; pole

Achtergrondinformatie:

In onderstaande figuur is op een geïdealiseerde manier een eenvoudige slingerbeweging weergegeven: een puntmassa m hangt aan een massaloos koord met lengte l.

We geven de slinger een uitwijkingshoek a tov van de verticale ruststand hetgeen betekent dat de massa een booglengte aL van de evenwichtspositie afraakt.De zwaartekracht zorgt er nu voor dat deze massa weer terugkeert naar de evenwichtspositie.  De kracht die uitgeoefend wordt kunnen we ontleden in twee componenten waarvan er een loodrecht op het koord staat, de grootte van die kracht is -mg.sina. De versnelling van de afgelegde weg is gelijk aan de 2de afgeleide van de verplaatste booglengte. 

Langs de boog gezien geldt de 2de wet van Newton: ma=F, dus:


Deze vergelijking is niet de vergelijking voor een eenvoudige harmonische beweging. De 2de afgeleiden van de verplaatsing (de hoek a) is niet evenredig met –a maar met –sina.

De hierboven afgeleide dv kent geen eenvoudige oplossing maar door gebruik te maken dat voor kleine hoeken van a geldt dat deze gelijk is aan de sinus kunnen we hem hanteerbaarder maken.

Indien a dusdanig klein is dat sina ~a geldt:

Dit is de algemene dv voor een harmonische oscillator met als  oplossing:

 

Waarbij a0 de uitwijking is die bij de start geldt.
Voor de hoekfrequentie geldt:

Waardoor voor de trillingstijd geldt dat:  

De slingertijd wordt dus bepaald door de lengte van het koord aangezien g op aarde nagenoeg constant is.

De slingertijd is de tijdsduur die verloopt tussen twee momenten waarop een punt (bijvoorbeeld de massa) van een slinger zich weer op hetzelfde uiteinde bevindt. 

De slingertijd wordt ook wel periode genoemd.

Uit de formule van de slingertijd kunnen we afleiden dat de periode van een slinger alleen maar afhankelijk is van de lengte van de slinger en de gravitatieconstante. Ook speelt de amplitudo niet een bijzonder grote rol zolang deze relatief klein is (sinusbenadering moet blijven gelden). Deze afhankelijkheid maakt het mogelijk de slinger als klok te gebruiken. 
 

16/01/2017