Constante van Planck


|
Constante van Planck |

|

|
Datum: Augustus - September 2010
Inleiding:
| Zoals gewoonlijk stond dit experiment stond al langer op mijn lijstje van uit te voeren experimenten. In dit geval was de trigger om het daadwerkelijk te doen de vraag of ik een workshop wilde verzorgen op het NVON TOA Congres op 11 November 2010 in Wageningen. De voorkeur ging uit naar een natuurkundig experiment, waarvan akte. |
Principe:
De constante van Planck bepalen m.b.v. de doorlaatspanning van Light Emitting Diodes (LED's).
Materiaal:
|
|
|
|
|
|
|
Experimentele opstelling:
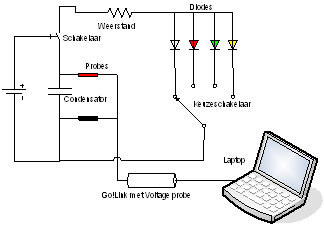
| Opstelling met Vernier Go!Link | |
|
De experimentele opstelling is schematisch
weergegeven in nevenstaande figuur (althans een geavanceerde versie). Een
eenvoudiger versie is te zien in onderstaande foto.
Als condensator heb ik gebruikt: Als weerstand heb ik gebruikt: |
 |
 |
|
| Meting met Vernier Go!Link Interface: | |
|
|
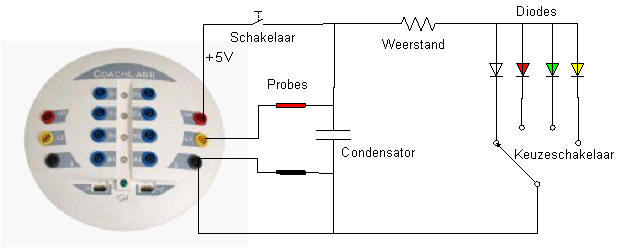
| Opstelling met CMA Coachlab | |
 |
|
|
 |
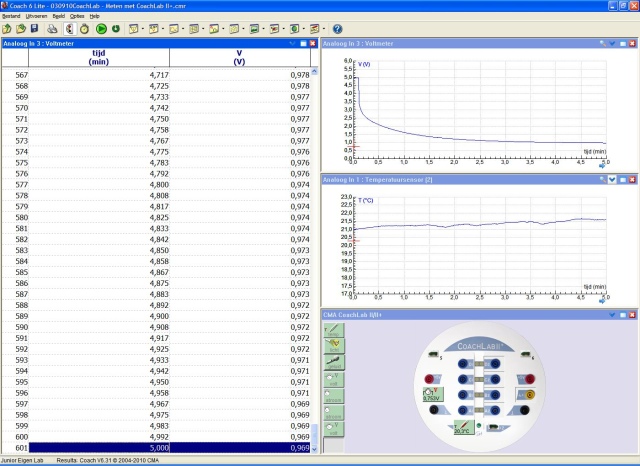 |
|
| Visuele bepaling van de grenswaarde | |
|
|
 |
 |
Resultaten:
| Eerste experiment op: 260810 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mijn eerste experiment heb ik uitgevoerd met
de spullen die ik op dat moment tot mijn beschikking had of waar ik snel aan
kon komen. Dat betekende uiteindelijk een beperking in het aantal kleuren
LED dat ik had (blauw, rood, groen, geel, IR) alsmede een beperking m.b.t.
de condensator capaciteit nl. 10000 uF. Ik heb, na wat experimenteren, ook
besloten om af te wijken van het voorschrift dat beschreven wordt in het
artikle van Zhou & Cloninger. Zij hebben hun systeem ontworpen op een
stroomsterkte van 60 mA (6V/100 Ohm = 60 mA). Na een LED opgeblazen te
hebben en wat literatuur over LED's gelezen te hebben kwam ik tot de
conclusie dat het beter was om op een stroomsterkte in de buurt van de 20 mA
te mikken. Dit betekent dat ik in dit eerste experiment met een RC tijd van
2.2 s te maken had i.p.v. de 25 s die in het artikel gebruikt werd. De
meetresultaten van dit eerste experiment zijn weergegeven in onderstaande
grafiek. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Deze meetwaarden worden vervolgens gebruikt om de constante van Planck te berekenen. Een foton gegenereerd door een LED g=heeft een energie van:
Hierin is f de frequentie van de elektromagnetische golf, c de lichtsnelheid (c = 299792458 m/s), l de golflengte, e is de lading van een elektron (e = 1.6022 x 10-19 C), V0 is de doorlaatspanning van de diode en h is de constante van Planck (h = 6.6260693 x 10-34 J.s). De RC curve die we gemeten hebben wordt geÔmporteerd in Excel kan gefit worden met de vergelijking:
Hierin zin A,
a en B
constanten, waarbij B de doorlaatspanning V0 die we willen berekenen en A de
spanning gemeten over de volle condenstor. De fit heb ik uitgevoerd m.b.v. een
eenvoudige chi2 toets en de solver die als Add-In in Excel zit. Men
berekent en kwadrateert eerst het verschil tussen de gemeten waarde en de
berekende waarde. Vervolgens sommeert men al deze waardes en gebruikt de Solver
om deze som te minimaliseren door A, B en a
te variŽren. Het is wel noodzakelijk om in eerste instantie redelijke schatting
voor de constantes op te geven. A en B kan men aflezen uit de grafiek en een
goede schatting voor a
is 0.3. Een voorbeeld van een dergelijke curvefit is weergegeven in
onderstaande figuur (IR LED). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Op deze manier kunnen we de doorlaatspanning van alle LED's berekenen uit de meetdata.Door vervolgens aan de hand van bovenstaande formule de energie van het foton uit te rekenen en deze uit te zetten tegen de frequentie kan men de constante van Planck berekenen uit de hellingshoek van de grafiek. Hierbij moet men er op letten dat de grafiek door 0 gaat. De resultaten van deze meting alsmede de resultaten die men in het artikel kon vinden zijn weergegeven in onderstaande tabel en grafiek. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Het resultaat is weergegeven in onderstaande tabel. Zoals men kan zien is er in deze eerste poging een relatief groot verschil tussen de berekende waarde en de werkelijke waarde. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tweede experiment: 290810 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
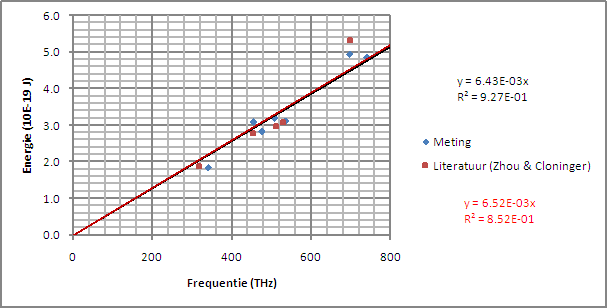
In dit tweede experiment heb ik een condensator
van 0.1 F gebruikt (RC tijd = 22 s). Ook heb ik twee extra LED, een oranje en
een UV led in het meetprogramma opgenomen. De resultaten zijn weergegeven in
onderstaande tabel en grafiek. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
De resultaten van dit experiment laten zien dat de combinatie van een groter golflengtegebied en een langere RC tijd een nauwkeuriger resultaat opleveren. De RC tijd is min of meer vergelijkbaar met de literatuurreferentie waarop dit experiment gebaseerd is. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Derde experiment: 030910 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Dit derde experiment heb ik dus met CoachLab uitgevoerd. Belangrijker is echter dat ik de meettijd verlengd heb naar 5 minuten. De resultaten suggereren echter dat dit geen positiev invloed uitoefent op het resultaat. Hierbij is het wel van belang zich te realiseren dat ik andere LED's gebruikt heb (nieuwe schakeling gebouwd). De resultaten zijn weergegeven in onderstaande tabel. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Men kan de constante van Planck aflezen uit de
regressielijn die gegeven wordt in de grafiek. Excel biedt echter een functie om
deze uit te rekenen. In dit geval kan men niet de SLOPE functie gebruiken
aangezien men deze niet kan dwingen door 0 te gaan. Met de functie LINEST kan
dit echter wel: LINEST(known_y's, [known_x's], [const], [stats]) Door op de plaats van [const] de waarde FALSE in te vullen wordt de hellingshoek berekend voor een lijn die door 0 gaat. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vierde experiment: 120910 & 140910 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In dit experiment probeerde ik te bepalen of een verandering in RC tijd (zowel langer als korter) een beter resultaat kan leveren. De 1 F condensator was echter maar ontworpen voor een spanning van 2.3 V. Voorzichtheidshalve heb ik daarom de voedingspanning verlaagd naar 4.5 V. De resultaten zijn weergegeven in onderstaande tabel. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Zoals men aan de resultaten kan zien heeft het verlengen of verkorten van de RC tijd geen significante invloed op de nauwkeurigheid van de bepaling. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Een reden voor een afwijkende resultaat kan zijn dat we de golflengte van het LED niet zo nauwkeurig kennen als we dachten. Na wat zoeken op het web lijkt dat inderdaad een bijdrage te kunnen leveren. De spectrale bandbreedte van een LED heeft een grootte orde van 20 tot 60 nm. Rekenen we dat om naar een relatieve fout dan vertaalt dit naar een relatieve fout 4 to 12 %, grofweg 8%. Deze fout is echter te minimaliseren door de golflengte van een LED exact te bepalen m.b.v. een spectroscoop die een gekalibreerde golflengte schaal bevat. Ik heb weliswaar een spectroscoop in mijn bezit maar deze bevat geen schaalverdeling. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vijfde experiment: 220910 - Visuele bepaling | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In dit experiment heb ik de drempelspanning visueel proberen te bepalen m.b.v.
de methode zoals die door Martin Hackworth beschreven wordt. De gedachte hierachter is dat ik wilde
controleren of de condensator methodiek die we in dit experiment hanteren
inderdaad een verbetering is t.o.v. andere methodes die in de literatuur
omschreven worden. Men wordt bijna onmiddellijk met twee nadelen geconfronteerd
als men dit experiment uitvoert:
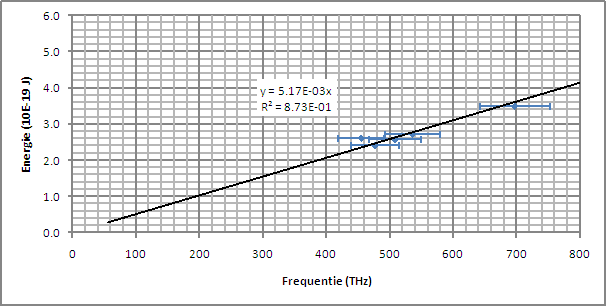
Het resultaat van dit experiment is weergegeven in onderstaande grafiek en tabel. De meetresultaten en berekening kan men vinden in de file: resultatenoverzicht.xsls |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Zoals men aan het resultaat kan zien is de afwijking die men heeft t.o.v. de werkelijke waarde het grootst in dit experiment hetgeen impliceert dat de onderzoeksmethode die we bezigen inderdaad een verbetering in nauwkeurigheid bewerkstelligd. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
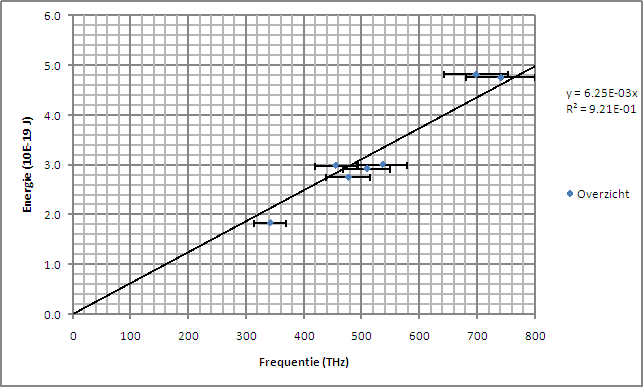
| Al met al lijkt het er dus op dat een meting met een weerstand van 220 Ohm en een Condensator van 0.1 F de beste resultaten oplevert. De vraag die nu overblijft is of we dit resultaat nog kunnen verbeteren. De beste methode daarvoor is te kijken of het enkele malen herhalen en vervolgens middelen inderdaad een verbetering bewerkstelligt. Hetgeen ik vervolgens gedaan heb. Zoals in onderstaande tabel te zien is heeft dit niet geleid tot een significante verbetering. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We vinden nu een waarde van 6.25 x 10-34 voor de constante van Planck, ca. 6% relatief onder de literatuurwaarde. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Discussie:
|
In 1900 probeerde de Duitse fysicus Max
Planck een model te ontwerpen dat het elektromagnetisch spectrum
beschreef dat uitgezonden wordt door een heet zwart lichaam (black body
radiation). Deze "black body radiation" is de straling die men kan zien
komen van de zon, de gloeidraad van een gloeilamp of van het element in
een elektrische oven. Om zijn model voorspellingen kloppen te krijgen
met de waarnemingen was hij genoodzaakt om een aanname te doen nl dat
elektromagnetische straling is gegroepeerd in kleine discrete eenheden
van energie die we tegenwoordig fotonen noemen. Bij elke frequentie
hebben deze fotonen een discrete energie die gegeven wordt door de
formule: E = h.f, waarin E de energie van het foton is in Joules, f de
frequentie in Herz en h de constante van Planck (6.626 x 10-34
J/s). Als men zegt dat Max Planck de basis legde voor een wetenschappelijke revolutie zal men vervolgens moeten zeggen dat Albert Einstein in 1915 deze revolutie completeerde door een fundament onder het model te leggen. Met de theorie die hij voorstelde, gebaseerd op fundamentele kwantummechanische principes, kon men niet alleen "black body radiation" verklaren maar ook een fenomeen dat al lang als een probleem beschouwd werd, het zgn. foto elektrisch effect. Bij het foto elektrisch effect kan men observeren dat indien een metalen kathode in een vacuŁmdiode door licht beschenen werd, er elektronen vrijkwamen uit dat rooster waarbij de kinetische energie van deze elektronen bepaald werd door golflengte van het licht dat op de kathode valt. Dit fenomeen kon men niet verklaren met de klassieke Newtoniaans fysica die op tot op dat moment als de fundamentele basis van de Natuurkunde beschouwd werd. De constante van Planck verschijnt keer op keer in kwantummechanische berekeningen. Men moet zich echter ook realiseren dat juist omdat de constante van Planck zo klein is (6.626 x 10-34 J/s) het klassieke Newtoniaanse model valide is voor de macroscopische wereld waarin wij ons bewegen. Een iets andere formulering is te stellen dat alhoewel een kwantummechanische beschrijving van de wereld de waarde h omvat, h dusdanig klein is dat het effect dat deze heeft verwaarloosbaar is in macroscopische situaties. Door het verwaarlozen van h reduceren we kwantum fysica tot klassieke fysica. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Een LED is opgebouwd uit een halfgeleider met een P-N grenslaag die licht uitzend als er energie in het systeem gestopt wordt. De lichtemissie kan verklaard worden op basis van de energie banden in de halfgeleiders. Als er een recombinatie van gaten en elektronen plaatsvindt in de grenslaag wordt energie omgezet in warmte of licht (fotonen). De stralingsfrequentie wordt bepaald door de materialen die gebruikt worden in de P-N laag. Door concentraties te variŽren kan men verschillende kleuren verkrijgen. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In vergelijking met de resultaten gerapporteerd door Zhou et al lijken we niet zulke mooie resultaten te halen. Bekijken we publicatie echter iets nauwkeuriger dan kunnen we lezen dat ze ze resultaten behaald hadden die varieerden van 5.77 tot 7.67 x 10-34. Wat betreft de resultaten vermeld in de tabel in het artikel kunnen we dus zeggen dat dit een typisch geval is van "only the best results are shown" en niet "typical results are shown". De resultaten die we in dit onderzoek gevonden hebben laten een soortgelijke range zien. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Van de andere methodes die in de literatuur vermeld worden gebruikt er een een voltmeter om de minimum spanning te meten die nodig is om het LED aan te zetten terwijl de andere de Vo bepaald door een IO-V curve van de LED te bepalen. Het probleem met beide methodes is dat in het ene geval het menselijk oog bepaald (NEI) wanneer de LED aangaat en men bij de andere het snijpunt moet afschatten uit een kromme. Deze methodes zijn daarom iets subjectiever hetgeen kan resulteren in een grotere foutenmarge. In de methode die we hier gehanteerd hebben bepalen we de ontladingscurve van een condensator door een LED dat in serie staat met een stroombegrenzende waarstand. De ontladingscurve nadert een een voltage dat constant is en ongelijk aan nul. Dit constante voltage (Vo) is het minimum voltage dat benodigd is om stroom te laten vloeien door de LED. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Alle meetresultaten nogmaals weergegeven in onderstaande tabel waaraan toegevoegd het gemiddelde van alle resultaten. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Conclusie:
|
Literatuur:
|
Opmerkingen:
|
Achtergrondinformatie:
|
LED's |
|||||||||
|
Light Emitting Diode (LED) staat voor, zoals
de naam aangeeft, een diode die licht afgeeft. Het licht dat een LED
uitstraalt wordt niet opgewekt door het verhitten van een draad zoals in een
gloeilamp gebeurd, maar door het aanslaan van elektronen in het halfgeleider
materiaal. |
|||||||||
| Halfgeleiders | |||||||||
|
Halfgeleidermateriaal is de grondstof voor
vele onderdelen in de moderne elektronica, zoals diodes, transistors en
lichtgevoelige weerstanden. Halfgeleiders zijn materialen, die de elektrische stroom matig geleiden. Het meest gebruikte halfgeleidermateriaal is silicium. Vroeger werd germanium veel gebruikt. Deze stoffen vormen kristallen met een zogenaamd diamantrooster, waarin elk atoom omringd wordt door 4 buurtatomen. De verbindingen met deze buuratomen worden door 4 elektronen uit de buitenste schil verzorgd. Deze elektronen zijn heel stevig gebonden aan hun atomen. Er is vrij veel energie voor nodig om ze los te krijgen. Daarom wordt bij kamertemperatuur maar een heel geringe fractie door de warmtebeweging 'losgemaakt'. Bij lage temperaturen komen helemaal geen elektronen vrij en bij 0 K is een halfgeleider een isolator. Als een elektron wordt losgemaakt, blijft er een atoom achter met een elektron tekort. Zo'n plaats waar een elektron ontbreekt noemt men een gat; het losgemaakte elektron heet vrij elektron. Door de warmtebeweging wordt gelijktijdig een vrij elektron en een gat gegenereerd, een proces dat men paarvorming noemt. Het gat kan op twee manieren worden opgevuld. Een vrij elektron kan de plaats opvullen, men spreekt dan van recombinatie. Hierbij verdwijnt dus een paar. Het gat kan echter ook worden opgevuld door een elektron dat hoort bij een buuratoom. Op deze manier kan een gat zich van atoom tot atoom verplaatsen. Als er een elektrisch veld heerst kan een gat zo bijdragen tot elektrische geleiding. Het gedraagt zich als een vrij bewegende positieve elektrische lading. In een halfgeleiderkristal worden voortduren paren gegenereerd, terwijl ook voortdurend paren verdwijnen door recombinatie. Bij een hogere temperatuur worden er meer paren gegenereerd dan bij een lagere temperatuur. De concentratie van vrije elektronen en gaten is dan groter, zodat de kans op recombinatie dan ook groter is. Bij elke temperatuur zal het aantal paarvormingen gelijk zijn aan het aantal recombinaties, maar bij hogere temperaturen zijn de aantallen groter. De elektrische geleiding in een hafgeleider wordt 'verzorgd' door vrije elektronen en gaten. Zolang het materiaal niet verontreinigd is, zijn er precies evenveel gaten als vrije elektronen. Zuiver materiaal noemt men wel intrinsiek. Als aan zuiver silicium een kleine hoeveelheid fosfor wordt toegevoegd, kunne de fosfor-atomen op silicium plaatsen in het rooster gaan zitten. Omdat fosfor 5 elektronen in de buitenste schil heeft, en er maar 4 nodig zijn voor de bindingen met de buuratomen, heeft elk fosforatoom een elektron over. Dit elektron kan vrij gemakkelijk worden losgemaakt: er is maar een kleine hoeveelheid energie voor nodig. Het gevolg is dat bij kamertemperatuur vele elektronen zich losmaken, onder achterlating van een positief fosfor ion, dat niet van zijn plaats kan. Het fosfor 'levert' dus vrije elektronen aan het silicium. Het wordt daarom donor genoemd. Het toevoegen van een stof als fosfor heet doping. In het silicium zelf treedt natuurlijk de zopas genoemde paarvorming op, waarbij evenveel vrije elektronen als gaten ontstaan. Aangezien er nu vele extra vrije lektronen aanwezig zijn, zullen door recombinatie maar weinig gaten overblijven, veel minder dan in intrinsiek silicium. Als silicium dus met een donor wordt verontreinigd, zullen in het silicium veel vrije elektronen en weinig gaten aanwezig zijn. De vrije elektronen zijn de meerderheidsladingsdragers; de gaten de minderheidsladingsdragers. Omdat elektronen een negatieve lading hebben, noemt men silicium dat met een donor verontreinigd is: n-type silicium. Men kan het silicium ook dopen met een element dat 3 elektronen in de buitenste schil heeft, zoals gallium. Een gallium-atoom heeft dan een elektron te weinig om alle bindingen met buuratomen te verzorgen. Het zal graag een elektron van een buuratoom willen opnemen, waardoor echter bij het buuratoom een gat ontstaat. Omdat er weinig energie voor nodig is om zo'n elektron op te nemen, zullen er veel gaten ontstaan. Het gallium wordt daarom een acceptor genoemd. Ook nu geldt dat de paarvorming gewoon doorgaat. Omdat er nu veel gaten zijn, zullen door recombinatie maar weinig vrije elektronen overblijven. de gaten (die zich gedragen alsof ze een positieve lading hebben) zijn de meerderheidsladingsdragers en de vrije elektronen de minderheidsladingsdragers. Men spreekt nu van p-silicium. Halfgeleiderdiode We beschouwen nu eerst een halfgeleiderdiode, waarop nog geen spanning is aangesloten. De ene helft van de diode bestaat uit p-materiaal en de andere uit n-materiaal. Omdat de concentratie gaten in het linkerdeel veel groter is dan rechts, zullen er geen gaten naar het rechterdeel gaan en daar recombineren met vrije elektronen; andersom zullen er vrije elektronen naar links gaan en daar recombineren. Hierdoor ontstaat er links een overmaat aan negatieve lading en rechts een overmaat aan positieve lading, waardoor een elektrisch veld ontstaat in de grenslaag. Over de grenslaag staat hierdoor een potentiaalverschil F.
In de grenslaag zelf blijven heel weinig vrije ladingsdragers over, ze zouden nl. direct kunnen recombineren. Men noemt de grenslaag daarom ook wel de depletielaag of uitputtingslaag. Door het elektrisch veld in de grenslaag wordt de gatenstroom van p naar n tegengewerkt, evenals de elektronenstroom van n naar p. Slechts een kleine fractie van deze meerderheidsladingsdragers heeft voldoende thermische energie om de grenslaag te passeren. Voor de minderheidsladingsdragers is de richting van het elektrisch veld juist gunstig. De (weinige) gaten in het n-materiaal kunnen dus allen de grenslaag over. Aangezien er voortdurend nieuwe paren gegenereerd worden, is er een kleine stroom gaten van n naar p. Zolang er geen uitwendige spanning wordt aangelegd, zal deze gatenstroom precies even groot zijn als die van p naar n. Het elektrisch veld in de grenslaag stelt zich automatisch zo in, dat er evenwicht is. Veronderstel nu, dat we het elektrisch veld in de grenslaag kleiner maken, door uitwendig een spanning aan te sluiten op de diode, met de pluspool aan de p-kant en de minpool aan de n-kant. De stroom van de minderheidsladingsdragers verandert daardoor niet, maar de fractie van de meerderheidsladingsdragers die de grenslaag kan passeren, wordt daardoor groter. Nu ontstaat er een netto elektronenstroom van n naar p. Dat betekent dat er een elektrische stroom (positieve lading) van p naar n loopt. De grootte van deze elektrische stroom hangt af van de aangelegde spanning, volgens
Hierin is I0 de elektrische stroom van de minderheidsladingsdragers, q de lading van het elektron, V de aangelegde spanning, k de constante van Boltzmann en T de absolute temperatuur. De eerste term van het rechter lid is de stroom van de meerderheidsladingsdragers; de tweede die van de minderheidsladingsdragers. De stroom van de meerderheidsladingsdragers neemt exponentieel toe met de aangelegde spanning. We kunnen het elektrisch veld in de grenslaag ook groter maken door de spanning andersom aan te sluiten. De stromen van de minderheidsladingsdragers veranderen daardoor niet, maar de fractie van de meerderheidsladingsdragers, die de grenslaag passeert, wordt kleiner. Als de spanning een paar Vol is, is deze fractie praktisch nul. Dan blijft dus alleen de stroom van de minderheidsladingsdrager over: Io. Deze stroom heet lekstroom of sperstroom. De elektrische stroom (positieve lading) loopt van n naar p. Omdat het aantal minderheidsladingsdragers dat per seconde gegenereerd wordt, sterk van de temperatuur afhangt, is de lekstroom ook sterk temperatuur-afhankelijk. De p-kant van de diode noemt men wel anode; de n-kant kathode. Als de pluspool van de spanning aan de p-kant is aangesloten, zeggen we, dat V>0 en dat de diode in doorlaatrichting is aangesloten. Is de pluspool aan de n-kant aangesloten, dan noemen we V<0 en is de diode in de sperrichting aangesloten. In het eerste geval is I>0 en in het tweede is I<0, volgens onderstaande formule:
We kunnen bovenstaande in een aantal figuren samenvatten.
In doorlaatrichting kan een diode in principe een grote stroom doorlaten, maar door zo'n stroom wordt een vermogen I*V in de diode afgegeven. Het hangt van het type af, hoeveel vermogen er gedissipeerd mag worden; wordt het toegestane maximum overschreden dan wordt de diode te heet en gaat hij kapot. Om deze reden ziet men vrijwel altijd in serie met een diode een weerstand, die de stroom begrenst. De lekstroom is zeer klein (in de orde van nA), zodat in principe vrij grote spanningen in de sperrichting aangesloten kunnen worden. Maar elke diode heeft een maximale spanning, waarboven doorslag in de grenslaag optreedt en de diode vernield wordt. Vaak is men meer geÔnteresseerd in de verandering is stroom als V een klein beetje verandert. Men noemt dit de differentiŽle of dynamische weerstand van de diode: r= dV/dI We kunnen de dynamische weerstand eenvoudig berekenen uit de bovenstaande formules, waarbij we de 1 verwaarlozen:
waaruit dus Ook de dynamische weerstand hangt dus van het instelpunt af. Gezien de afwijking van de diode ten opzichte van de theorie zal ook deze r slechts een benadering van de werkelijkheid zijn. In de Zener-diode wordt gebruik gemaakt van het "doorslaan" van de diode in de sperrichting. Hij is zo gemaakt, dat dit bij een goed gedefinieerde spanning gebeurt. De stroom kan dan in een vrij groot gebied variŽren, terwijl de spanning over de diode nauwelijks verandert. Door deze eigenschap kan hij gebruikt worden voor het leveren van een stabiele spanning. Het is natuurlijk wel zaak te zorgen dat de stroom niet te groot kan worden. Daarvoor wordt meestal een serieweerstand gebruikt. Zener diodes zijn te verkrijgen in waarden die variŽren van een paar Volt tot 75 Volt. |
|||||||||
|
Max Planck
Max Planck (1858-1947) was een Duits fysicus die tegenwoordig beschouwt wordt als een van de grondleggers van de kwantum mechanica door te postuleren dat energie bestaat uit kwanta. Vanuit deze premisse leidde hij in 1901 de universele stralingswet af. Hij was een professor in de fysica in Kiel en in Berlijn. Hij was de auteur van ondertussen als klassiekers beschouwde boeken over theoretische fysica zoals "Theory of Heat Radiation". In 1918 werd hem de Nobelprijs in Natuurkunde toegekend. |
|
||||||||
08/11/2010