Wet van Archimedes

Datum: September 2006

Principe:

Met een veerbalans, gewichten en water de Wet van Archimedes aantonen.

Materiaal:

  • veerbalans
  • statief
  • gewichten
  • water
  • spiritus
  • bekerglas
  • balans
  • schuifmaat

Uitvoering:

  • Hang de veerbalans aan het statief
  • Neem een cylindervormig gewicht en weeg het
  • Meet de diameter en de hoogte
  • Hang het gewicht aan de veerbalans en bepaal daarmee het gewicht
  • Laat het gewicht terwijl het aan de veerbalans hangt in het bekergals dat gevuld is met water zakken en bepaal wederom het gewicht
  • Herhaal dit met een ander gewicht en een gewicht met een andere metaalsoort 


meting in lucht      meting in water

Meetresultaten en uitwerking:

De resultaten en uitwerkingen zijn samengevat in onderstaande tabel en in een spreadsheet metingen.xls.

Discussie en conclusie:

De Wet van Archimedes stelt dat de opwaartse druk die een voorwerp in het water ondervindt gelijk is aan het gewicht, van het door het lichaam verplaatste water. Dit betekent dat er een lineaire relatie moet zijn tussen het volume van het voorwerp en de gewichtsafname die een voorwerp ondervindt bij onderdompeling in water.
Vatten we bovenstaande resultaten samen in een tabel:

Dan kunnen we onderstaande grafieken maken:
 
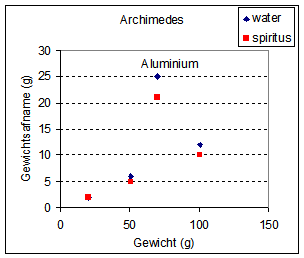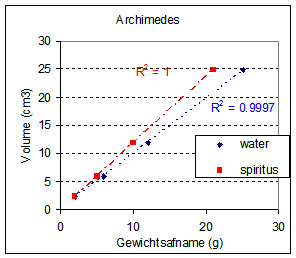De grafieken laten zien dat gewichtsafname inderdaad gecorrelleerd is met het volume van het lichaam en niet met de massa van het lichaam of materiaalsoort en bevestigen dus de Wet van Archimedes. We zien ook dat de dichtheid van het oplosmiddel ook een rol speelt. Dat klopt aardig met de definitie van de zgn Archimedeskracht zoals die in Wikipedia gegeven wordt:

Het gewicht van de verplaatste vloeistof of gas is gelijk is aan de zwaartekrachtversnelling (g) maal de dichtheid van de vloeistof of gas waarin het voorwerp zich bevindt (ρ) maal het volume van het voorwerp (V).

In formule:

archimedeskracht=F_{G (verpl. gas/vloeistof)}=g . \rho_{gas/vloeistof} . V \!
 
Op basis van de Wet van Archimedes kan men de volgende regels formuleren:
  • Een voorwerp zinkt in een vloeistof als de soortelijke massa van dat voorwerp groter is dan de soortelijke massa van die vloeistof (steen in water).
  • Een voorwerp zweeftt in een vloeistof als de soortelijke massa van dat voorwerp gelijk is aan de soortelijke massa van die vloeistof (uitgebalanceerde duikboot).
  • Een voorwerp drijft op een vloeistof als de soortelijke massa van dat voorwerp kleiner is dan de soortelijke massa van die vloeistof (kurk op water).
  • Drijft een voorwerp op een vloeistof, dan steekt zoveel van het voorwerp onder de vloeistofspiegel, dat de opwaartse kracht van de verplaatse vloeistof gelijk is aan het gewicht van het hele lichaam.

Opmerkingen:

  • We hebben hier materialen met dezelfde vorm getest. Het onderzoek kan uitgebreid worden met andere vormen, nog meer materialen en nog meer oplosmiddelen.

  • Een veerbalans (weegschaal gebaseerd op een veer die je in de betere "doe-het-zelf" zaak kunt kopen), is ook geschikt voor deze experimenten.

  • Indien met voorwerpen wil werken die een onregelmatige vorm hebben kun je het volume niet berekenen door het op te meten. Je kunt het volume echter op twee manieren bepalen. Een methode is door het in een maatcylinder gedeeltelijk gevuld met vloeistof te leggen en zo de volumetoename te meten. De andere methode is door een overvloeivat te gebruiken. Vul een bekerglas tot de rand met water. Plaats het voorwerp er voorzichtig in en vang zorgvuldig het water op dat over de rand spoelt. Door dat water nu te wegen en die massa met dichtheid van water te combineren (1 g/ml) kan men het volume van het voorwerp uitrekenen.

Literatuur:

  • G. PLoeger en J.H. Raat; 'Experimentele natuurkunde voor het Mulo/Mavo 1'; Noordhoff; 19??; p. 55-66.

  • Robert Gardner; 'Experimenting with Water'; Dover; 1993; ISBN 0486434001; p. 65-68.

  • JC Alders; 'Jongens en Natuurkunde'; Thieme; 1936; p. 136, 137.

Relevante websites:

Achtergrondinformatie:

Archimedes was een bekend Grieks filosoof die leefde van 287-212 voor Christus in Syracuse. Hij week in zoverre van andere Griekse filosofen af dat hij het niet alleen bij redeneren hield maar ook daadwerkelijk experimenten uitvoerde. Veel uitvindingen, ontdekkingen en verhalen zijn aan zijn naam gekoppeld. De juistheid is niet altijd te achterhalen.

Het verhaal achter de "Wet van Archimedes" is een van de beroemdste.

Koning Hieroon van Syracuse wilde een gouden krans offeren aan de goden en gaf aan een kunstenaar opdracht deze te maken. Nadat de krans aan koning was overgedragen twijfelde deze eraan of deze wel van puur goud was. Misschien was deze wel gemaakt van een mengsel van zilver en goud, een truuk waarvan valsemunters toen al gebruik maakten om munten te vervalsen. De koning vroeg aan Archimedes of deze kon vaststellen of de krans van puur goud gemaakt was zonder deze te smelten.
 

In gedachten verzonken liep Archimedes naar huis en besluit ter ontspanning een bad te nemen. Terwijl Archimedes zich in het bad laat zakken realiseert hij zich dat hij lichter wordt.  Goud heeft een hogere dichtheid dan zilver, een gouden krans heeft dus een kleiner volume dan een even zware zilveren krans. Uit de opwaartse kracht van het water zou hij dus het volume van de krans moeten kunnen bepalen en door dat te combineren met het gewicht van de krans zo vaststellen of de krans uit zuiver goud gemaakt was of uit een mengsen van zilver en goud. Volgens de legende vliegen deze gedachten door zijn hoofd en volgens de legende is hij zo blij dat hij het probleem heeft opgelost dat hij uit het bad springt en zonder zich aan te kleden naar de koning rent onder het uitroepen van "Eureka, Eureka" (Ik heb het gevonden, ik heb het gevonden).

11-01-2017