

| Opnemen van de capaciteit, oplaadkromme en ontlaadkromme van een condensator |  |
 |
Date : 07-09-1988
Principe:
| De oplaadkromme van een condensator geeft het verloop aan van de condensatorspanning als functie van de tijd. Om de oplaadkromme op te nemen moeten we dus de condensatorspanning en de tijd meten. |
Meetschema's:
 |
|
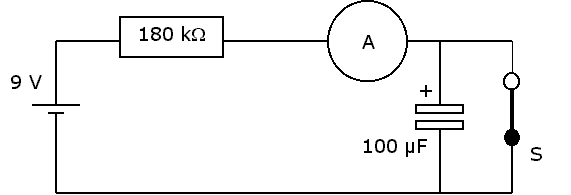
Schema RC tijd meting |
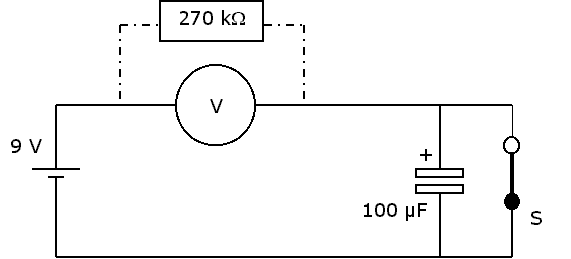 |
| Schema capaciteitsmeting |
Benodigd:
|
|
Werkwijze:
| Het meten van de condensatorspanning doen we niet direct, zoals de
meetschakeling al aangeeft. De weerstand van een condensator betreft nl alleen
de lekweerstand die heel hoog kan zijn. Indien we dan een voltmeter aansluiten
over de condensator dan beďnvloedt deze de meting teveel. We kiezen daarom voor
indirect meten. We meten de oplaadstroom en berekenen daarmee de spanning over de weerstand van 180 kOhm. Deze trekken we van de batterij af en vinden zo de condensatorspanning. De schakelaar S is bedoeld voor het meten van de oplaadstroom als de condenstor nog niet geladen is (t=0). Deze beginstroom vloeit alleen op het moment dat de batterij wordt aangesloten. De multimeter is vanwege zijn traagheid te laat om de waarde ervan aan te geven. Door de schakelaar te sluiten kan de condensator zich echter niet opladen, zodat de beginstroom blijft vloeien en rustig kan worden afgelezen. De maximale stroom vloeit als C nog ongeladen is. de batterijspanning staat dan geheel over R = 180 kOhm, dus Imax = 9 V / 180 kOhm = 50 µA.
Evenals voor de oplaadkromme van een condensator moeten we voor het opnemen van de ontlaadkromme de tijd en de spanning over de condensator meten. Ook hier voeren we via stroommeting een indirecte spanningsmeting uit om zo weinig mogelijk invloed van de meter te verkrijgen.
De werkelijke capaciteit van een elektrolytische condensator kan sterk afwijken van de opgegeven waarde, vaak 10-50%. Een eenvoudige methoden voor het meten van de capaciteit is de volgende. We gebruiken de weerstand van de multimeter, die als voltmeter is geschakeld, om een RC-schakeling met de te meten capaciteit te verkrijgen.
|
|
|
|
Meetresultaten en Discussie:
| De theoretische RC tijd kunnen we berekenen nl: 180000 Ohm * 100/100000 F =
18 s De echte weerstandswaarde kun je ook vaak met een goede multimeter bepalen, in dit geval: 178.9 kOhm. De gemeten onbelaste voedingsspanning is: 8.54 V De bepaalde capaciteit van de condensator is: 107.6 µF
De curves, model en meetresultaat in een plaatje uitgezet. In het model zijn de bepaalde waarde voor R en C ingevuld in de formule zoals deze in de achtergrondinformatie is afgeleid:
Zoals we kunnen zien komen theorie en werkelijkheid aardig overeen. Het verschil wordt voornamelijk bepaalt door de onnauwkeurigheid in het bepalen van Io,vnl. veroorzaakt door de traagheid van de multimeter tijdens het meten. Alle resultaten zijn opgeslagen in een gezipte excel-file: rcresults.zip Omdat het dieelectricum van een condensator niet ideaal is, zal bij een opgeladen condensator een lekstroompje vloeien van de ene plaat naar de andere. Zoals aan de meetresultaten te zien valt, meten we automatisch de lekstroom van de elco. De gemeten lekstroom: 0.1934 µA. |
Literatuur:
|
Achtergrondinformatie:
In de praktijk heeft men dagelijks te maken met
tijdsconstanten, (meestal met meerdere tijdsconstanten in combinatie met andere
factoren). Als voorbeelden kunnen we noemen:
Dit
natuurkundig verschijnsel treedt ook op bij RC combinaties. In een RC combinatie
is een weerstand in serie met een condensator via een schakelaar aangesloten op
een spanningsbron. In de getekende stand zal over de condensator en over de
weerstand geen spanning staan (UR=UC=0). Wordt de schakelaar (S1) op het tijdstip t=0
gesloten, dan zal door het circuit een stroom vloeien, die men als volgt kan
weergeven: De eenheid waarin RC wordt uitgedrukt is s
(seconden) Afleiding vergelijking Op elk willekeurig tijdstip geldt:
UR en UC zijn momentele
variabelen dus tijdsafhankelijk. De maximale spanning staat dus over de
weerstand op het tijdstip t=0. Volgens de wet van Ohm vloeit er dan ook de
maximale stroomsterkte. Tabel: UR en UC in % van
Utot
|
17-01-2017