De brug van Wheatstone

Datum : februari 2002

Principe:

Het in evenwicht brengen van een brug van Wheatstone.

Meetschema:

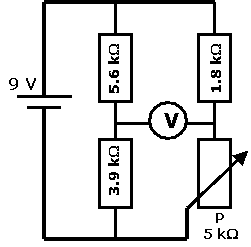
Benodigd:

Werkwijze:

Bouw de schakeling op zoals in het meetschema weergegeven (zie ook de foto hiernaast). Zet de spanning aan, en kijk naar de spanning die de multimeter aangeeft. De uitslag kan zeer klein zijn maar wel positief of negatief. Wordt er een waarde aangegeven, draai dan aan de potentiometer, totdat de multimeter 0 aangeeft.  Let er op dat de multimeter deze waarde ook in het laagste bereik aangeeft, zodat het brugevenwicht het meest nauwkeurig is ingesteld.

Discussie en conclusie:

Wordt een schuifweerstand met zijn eindpunten tussen de polen van een batterij opgenomen, dan zal het potentiaalverschil tussen een eindpunt en het sleepcontact, afhankelijk zijn van de plaats van het sleepcontact (zie Figuur 1).

Figuur 1	Figuur 2

Neemt het sleepcontact de stand C in, dan wordt de schuifweerstand verdeeld in twee weerstanden en wel: R_AC = R1 en R_BC = R2.

Nu is: V_AC = I.R1 en V_BC = I.R2

Bouwt men nu in hetzelfde circuit een tweede schuifweerstand in PQ parallel aan de reeds aanwezige en neemt men tussen de beide sleepcontacten C en R een volt- of amperemeter op, dan zal deze meter 0 aanwijzen als V_AC = V_PR (Figuur 2). De punten A en P hebben dezelfde potentiaal en de punten C en R hebben dezelfde potentiaal. Als V_AC = V_PR dan is tevens V_BC = V_RQ. Stellen we R_PR = R3 en R_RQ = R4 dan geldt:

(1)    I1.R1 = I2.R3 --> I1/I2 = R3/R1

(2)    I1.R2 = I2.R4 --> I1/I2 = R4/R2

(1) + (2) --> R3/R1 = R4/R2 --> R1.R4 = R2.R3 --> R1 : R2 = R3 : R4

Hieruit volgt:

1. kennen we 3 weerstanden dan kunnen we de 4de weerstand berekenen
2. kennen we 1 weerstand en de verhouding van de anderen dan kunnen we de 4de weerstand berekenen.

Deze methode van weerstand meten m.b.v. een zgn "stroomloze" brug is beken geworden onder de naam "Brug van Wheatstone", ofschoon Hunter Christie de eigenlijke ontdekker van deze techniek was.

In bovenstaande brug van Wheatstone bevindt zich een regelbare weerstand (P) van 5 kW. Door zijn waarde tussen 0 W en 5kW te regelen met een kleine schroevendraaier kan die brug in evenwicht worden gebracht.   

Bij evenwicht geldt P * 5.6 kW = 1.8 kW * 3.9 kW. 
Delen we links en rechts door 5.6 kW dan is P =  1.25 kW.   

Op deze manier kunnen we dus de waarde van een onbekende weerstand bepalen.

Opmerkingen:

• De brug van Wheatstone is een brugschakeling waarmee men zeer kleine weerstanden of weerstandsveranderingen kan meten. Ideaal is een volkomen symmetrisch opgebouwde brug van Wheatstone. Niet alleen de weerstanden in de brug maar ook de verbindingsleidingen van en naar de brug dienen zo symmetrisch mogelijk te zijn. Dat wil zeggen dat de elementen dezelfde soortelijke weerstand, doorsnede, lengte en temperatuur coëfficiënt moeten hebben om een optimaal meetresultaat verkrijgen.
• Een gewijzigde techniek; 'de stroomvoerende brug van Wheatstone' bestaat hierin dat 3 weerstanden van de brug exact bekend zijn (bv R1,R2 en R3 in Figuur 2). In plaats van de voltmeter wordt nu een ampèremeter ingebouwd. Op de plaats van R4 worden nu ijkweerstanden ingebouwd en de uitslag van de stroommeter afgelezen bij iedere ijkweerstand. Op deze manier vindt men een relatie tussen de uitslag van de stroommeter en de ingebouwde weerstand. Het is dus mogelijk om de stroommeter te gebruiken als weerstandsmeter door de afleesschaal uit te drukken in Ohm. Door nu een onbekende weerstand op de plaats van R4 in de schakeling op te nemen, zal uit de uitslag van de stroommeter de weerstand te berekenen zijn. 

Literatuur:

• A. Schommers; Elektronica echt niet moeilijk, deel 1: experimenten met gelijkstroom; Elektuur BV; 1988; ISBN 9070160358; p 62.
• A.J.Dirksen; Leerboek Elektronica, Deel 1 Gelijkstroomtheorie; De Muiderkring; 1979; ISBN 9060821017; p 96.

Relevante websites:

• Brug van Wheatstone
• De brugschakeling
• Using Thevenin Equivalents on Wheatstone Bridge
• Wheatstone Bridge

Achtergrondinformatie:

Een van de toepassingen voor een brug van Wheatstone is in de gaschromatografie. Een geleidbaarheidsdetector (TCD of khatarometer) werkt op basis van een brug van Wheatstone.

06-04-2003