

| Kinetiek experiment met bruistabletten. |  |
 |
Principe:
| Het bepalen van de invloed van de temperatuur op de reactiesnelheid van Alka-Seltzer in water met behulp van temperatuur en tijdsmetingen. |
Beschrijving:
|
De reactiesnelheid is de tijd benodigd voor een hoeveelheid reactanten om omgezet te worden in een product. De reactiesnelheid wordt door vele factoren bepaald waaronder de aard van de reactanten, hun concentratie, de temperatuur, katalysator aan- of afwezigheid en de druk (indien gassen een rol spelen). Alka-Seltzer tabletten bevatten warmtebehandelde natrium bicarbonaat, citroenzuur and een salicylaat. In water vindt dan de volgende reactie plaats: 3NaHCO3(s) + H3C6H5O7(s) + H2O(l) à C6H5O7Na3(aq) + 4H2O(l) + 2CO2(g) Aangezien het CO2 uit het water ontwijkt is het geen evenwichtsreactie maar een reactie van het type Aà B. |
Materiaal:
|
|
Uitvoering:
|
Meetresultaten en uitwerking:
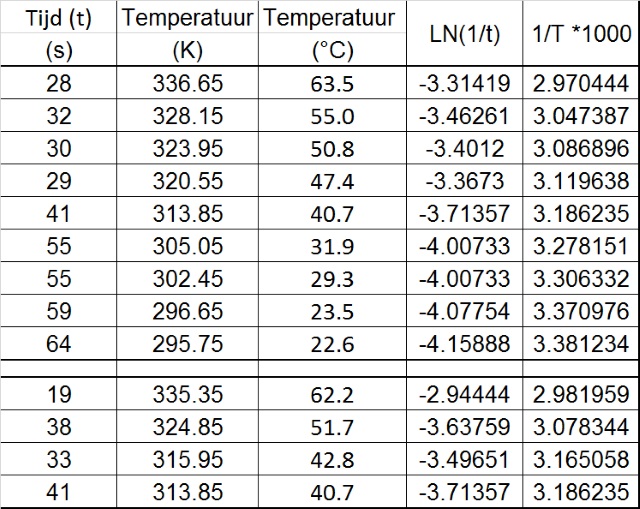
Berekeningen in zipped excelfile: seltzer.zip |
Discussie en conclusie:
|
Zoals te zien aan de resultaten zijn deze niet erg mooi. De spreiding in
resultaten is groter dan we in de literatuur vinden, alhoewel daarvoor
natuurlijk de aloude publicatie regel van "only the best results are shown" kan gelden. De
spreiding kan ook veroorzaakt worden doordat de experimenten over verschillende
dagen verspreid zijn uitgevoerd. Het is mogelijk dat als we omgevingstemperatuur
en watervolume iets beter constant houden de meetresultaten
reproduceerbaarder worden. Nog mooier zou het zijn om een eenduidig eindpunt te
kunnen definiëren. Dus: dit experiment overdoen met een beter gedefinieerd eindpunt van de reactie. Volgens de literatuur liggen de waardes van de activeringsenergie van reacties in oplossingen tussen de 8 en 150 kJ/mol. In eerdere experimenten(2) zijn de volgende waardes voor de verschillende soorten bruistabletten gevonden:
|
Opmerkingen:
|
Literatuur:
|
Relevante websites: |
Achtergrondinformatie:
|
De Arrheniusvergelijking:
met: k = reaktiesnelheidskonstante Dat
de verhoging van de temperatuur een sterke versnellende invloed heeft op bijna
alle chemische reakties is een feit uit de dagelijkse ervaring. Op dit principe
is nl. het koken van ons eten gebaseerd. Zijn aardappelen bij 100 °C
in ca. 20 min. gaar, bij 80°C zijn ze na uren nog hard. Van
't Hoff gaf als regel, dat de reaktiesnelheid twee- tot driemaal stijgt bij
verhoging van de temperatuur met 10 °C. Aan
de hand van experimentele gegevens stelde Arrhenius een formule op die de
relatie tussen snelheidsconstante en temperatuur weergeeft:
waarin
k de snelheidsconstante, T de temperatuur in Kelvin, Ea de
activeringenergie, A de frequentiefactor of pre-exponentiële factor en R de
gasconstante. De
evenwichtsconstante K van een reactie is afhankelijk van de reactieenthalpie DH
en de absolute temperatuur. De isochoor van Van ’t Hoff (constant volume)
geeft hiervoor:
K
kunnen we ook schrijven als k1/k-1 (de k’s van de
heengaande en teruggaande reactie) en DH kunnen we schrijven als Ea-Ea’:
Arrhenius
splitste bovenstaande in twee afzonderlijke vergelijkingen:
In
het algemeen geldt dan:
Een
voor de hand liggende gedachte om de observatie van de
temperatuurafhankelijkheid te verklaren is met de botsingstheorie. Is het aantal
botsingen is nu ook verdubbeld? Volgens de kinetische gastheorie neemt het
aantal botsingen bij een temperatuur verhoging van 10°
slechts 1-1.5% toe (de evenredigheid van het botsingsgetal met Ö(T).
Deze verklaring is dus niet afdoende. Daarnaast
speelt een ander probleem deze verklaring parten. Gebruiken we de kinetische
gastheorie om het aantal botsingen per seconde (Z) te berekenen: Zn
= ˝ Ö
(2 P
d˛ n˛ v) d
= diameter n
= aantal deeltjes per volume-eenheid v
= de gemiddelde snelheid Voor
de gemiddelde snelheid kan men afleiden:
M
= molecuulmassa. Dan
krijgen we voor voor Z:
Dan
zouden al snel tot de conclusie
komen dat, indien alle deeltjes bij een botsing reageren bij 1 bar en kamertemp
de omzetting al na ca. 10-8 s voor 99.9 % zou zijn verkopen (k=1011).
Dit gegeven is niet conform het langzamer verloop die wij kennen. Arrhenius
loste dit probleem op door te veronderstellen dat slechts een deel van de
reactiemoleculen daadwerkelijk actief is. Deze moleculen hebben een hogere
energie-inhoud, de activeringsenergie (voornamelijk in de vorm van
trillingsenergie). Anders geformuleerd kunnen we stellen dat de
activeringsenergie de minimale kinetische energie is die reactanten moeten
hebben om producten te kunnen vormen. Passen
we de wet van Boltzmann toe dan formuleren we voor de fractie van het
aantal deeltjes met een energie groter dan Ea:
Het
aantal moleculen dn/dt dat per tijdseenheid wordt omgezet zal nu gelijk
zijn aan het product van dp/p en het botsingsgetal:
Deze
formule is echter alleen geldig voor bimoleculaire reacties in de gasfase tussen
gelijke moleculen. We
kunnen echter afleiden dat:
Vergelijken
we deze formule met de Arrheniusformule dan geldt voor de pre-exponentiële
factor A:
|
16/01/2017