Bouwpakket spectroscoop


|
Bouwpakket spectroscoop |
 |
 |
Datum: augustus 2004
Principe:
Bouwpakket om een spectroscoop te bouwen waarmee we het spectrum van een lichtbron bestuderen.
Materiaal:
|
|
|
Het bouwpakket is te bestellen bij http://www.experimentalchemie.de.
De prijs is € 6,- exclusief verzenkosten. Inclusief verzendkosten wordt het dan ca. € 10. Als je een bestelling doet op de site krijg je het bedrag en de benodigde overboekingsgegevens voor een internationale transactie toegestuurd. Bij de meeste banken hoef je niet extra te betalen voor een overboeking naar het buitenland. Bij sommige banken kun je via je PC banking programma een boeking naar het buitenland doen. |
Uitvoering:
|
|
|
|
|
|
|
|
|
|
|
Gebruiksaanwijzing:
|
Houdt de spleet richting een lichtbron. En
kijk door de lens. Beweeg de lens op en neer totdat het spectrum op de
schaalverdeling valt.
Een heldere lichtbron zal een eenvoudig spectrum laten zien zonder scherpe lijnen. De reden is dat het licht van een hete vaste stof komt (het wolfraam filament in de gloeilamp) Hete gassen produceren licht dat maar uit een paar kleuren is opgebouwd. Een spectroscoop zal deze kleuren uit elkaar halen waardoor ze apart zichtbaar worden. In de tabel hierbeneden wordt de samenhang tussen kleur en golflengte gegeven zoals deze ook op de schaalverdeling van de spectroscoop te zien is. |
| kleur | golflengte (nm) |
| rood | 650 |
| oranje | 600 |
| geel | 575 |
| groen | 550 |
| blauwgroen | 500 |
| blauw | 450 |
| paars | 400 |
Resultaten
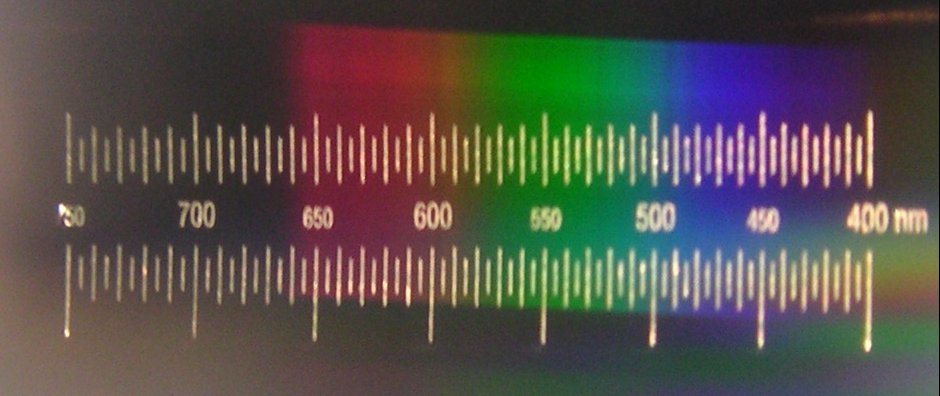 |
 |
| spectrum van de zon | spectrum van een lamp |
Opmerkingen:
Literatuur:
Relevante websites:
Minder relevante websites
Achtergrondinformatie:
|
Spectra Zeer veel spleten naast elkaar vormen een tralie of rooster. Als je monochromatisch licht op een tralie laat vallen dan ontstaat een stelsel van lijnen, het zgn interferentiepatroon. Een tralie kan worden gemaakt door zwarte lijnen op een witte achtergrond fotografisch sterk te verkleinen. Hoe dichter de spleten bij elkaar zitten, hoe wijder het patroon zal worden en hoe nauwkeuriger de golflengtes bepaald kunnen worden. |
|
enkele spectra |
|
 |
wit licht |
|
|
stikstof |
|
|
waterstof |
|
|
natrium |
| Roostertheorie
Een buigingsrooster bestaat uit een vlakke glazen plaat met hierop een dunne laag aluminium gedampt. Hierin zijn een groot aantal evenwijdige krassen op onderling gelijke afstand aangebracht. Hierdoor wordt een buigingsbeeld verkregen. De roosterconstante d is de afstand tussen twee opeenvolgende krassen. In het buigingsbeeld zien we bij monochromatisch lucht een aantal heldere gekleurde lijnen waartussen het donker is. Bij wit licht nemen we aan weerszijden van de heldere witte lijn, het centrale maximum, een aantal volledige spectra waar. Om dit buigingsbeeld te verklaren gebruiken we de opstelling zoals die oorspronkelijk door Fraunhofer gebruikt werd waarbij de belichting van het rooster plaatsvindt door een evenwijdige monochromatische lichtbundel en een lens (L) achter het rooster (T) geplaatst is. Deze lens zorgt voor de afbeelding van het interferentiebeeld in het brandvlak van de lens zoals hierbeneden is weergegeven. |
|
|
|
We kunnen de theorie van Huygens gebruiken om het verband af te leiden dat bestaat tussen de ligging van de ontstane heldere lijnen en de gebruikte golflengte (l). Aangezien er een evenwijdige luchtbundel loodrecht op het rooster valt zijn alle punten (1...6) onderling in dezelfde fase en zijn nieuwe trillingscentra die in alle richtingen golven uitzenden. De golven die rechtdoor gaan komen in fase in het hoofdbrandpunt P samenkomen. In dit punt zal vanwege de optredende versterking maximale lichtintensiteit heersen (centrale maximum). Golven die onder een hoek a worden uitgezonden lopen tot de lijn CD allemaal verschillende optische wegen (de weglengte is verschillend) zodat ze op deze lijn allen een verschillende fase hebben. Vanaf CD tot P' wordt wel dezelfde weg afgelegd, hetgeen betekent dat het onderlinge faseverschil gehandhaafd blijft. |
|
In P' zal weer maximale
intensiteit optreden als het weglengteverschil tussen twee opeenvolgende
spleten tot aan de lijn CD een verschil heeft van 1 golflengte (de punten
op de lijn hebben dan dezelfde fase). Uit bovenstaande figuur kun je dan
afleiden: |
|
17-01-2017