Afkoeling volgens Newton


|
Afkoeling volgens Newton |
 |
 |
Datum:
april 2003
Principe:
| Het afkoelen van water meten gedurende een bepaalde tijd. |
Beschrijving:
|
Zodra er hete koffie in een kop wordt gegoten begint deze af te koelen.
Het afkoelingsproces verloopt eerst heel snel en daarna langzamer. Na een lange
tijd is de temperatuur van de koffie hetzelfde als die van de omgeving. De
temperatuur variaties van afkoelende lichamen werd samengevat door Newton in
zijn warmtewet. De snelheid waarmee de temperatuur van een voorwerp verandert is
evenredig met het verschil tussen de constant veronderstelde
omgevingstemperatuur en de ogenblikkelijke temperatuur van het voorwerp. Oftewel: DT/Dt = k(T-Ts) waarin DT het temperatuurverschil gedurende een zeer kort tijdsinterval Dt. T is de temperatuur van het object op een gegeven tijdstip. Ts is de omgevingstemperatuur en K is een proportionele constante. Indien we de vergelijking mathematisch oplossen krijgen we: T-Ts = (T-T0)e-kt waarbij T0 is de temperatuur van het object op t=0. Met dit experiment onderzoeken we de afkoeling van een object en verifiëren de afkoelingswet. |
Materiaal:
|
|
Uitvoering:
|
Meetresultaten en uitwerking:
|
De Lego Mindstorms RCX was geprogrammeerd om elke 15 s de temperatuur te
meten (zie Appendix). De meetresultaten kunnen worden gevonden in de excel file afkoeling.xls en worden weergegeven in onderstaande grafiek. |
|
|
Discussie:
|
Volgens Newton's wet van afkoeling geldt voor
een voorwerp dat afkoelt o.i.v. geforceerde convectie (luchtstromingen) dat de
snelheid van afkoeling evenredig is met het verschil in temperatuur tussen het
voorwerp en zijn omgeving. Aangezien het temperatuurverschil evenredig is met de
verandering in warmte:
waarin dT/dt
de afgeleide van de temperatuur in de tijd is, Ts de
omgevingstemperatuur en K een evenredigheidsconstante. Deze vergelijking kunnen
we integreren waarbij we stellen dat op het tijdstip t=0 de temperatuur van het
voorwerp T0 is.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| We willen dus bovenstaande formule aan de waarnemingen
koppelen waarbij K berekend wordt mbv van de meetresultaten. We kunnen de bovenstaande gelineariseerde versie toepassen maar dat is niet nodig. We kunnen K bepalen m.b.v. de solver (of oplosser) in excel in combinatie met een eenvoudige chik^2 toets. In het kort gezegd berekenen we bij elk tijdspunt waarvan we een meting hebben de bijbehorende temperatuur door eerst een K te schatten (bv 0.001). We bereken dan het verschil tussen gemeten en berekende waarden en kwadrateren dat. Alle kwadraten tellen we bij elkaar op. M.b.v. de solver minimaliseren we de som door de K die we in de berekeningsformule gebruiken te wijzigen. Het geheel ziet er dan uit als in onderstaande tabel, waarbij de resultaten van 3 tijdstippen te zien zijn. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
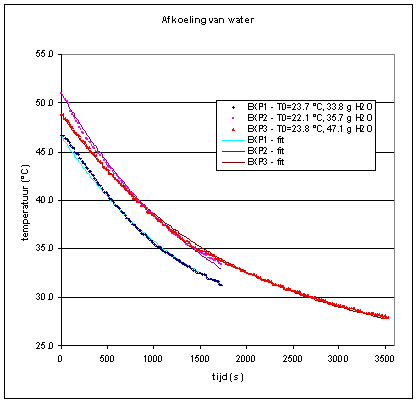
| Het resultaat kunnen we zien in onderstaande grafiek. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In de grafiek is goed te zien dat de berekende curves goed overeenkomen met de
gemeten curves. Voor de curve-fits hebben we de echter verschillende K's berekend nl: EXP1 0.001325638 EXP2 0.001307257 EXP3 0.001232084 Alhoewel de verschillen in K klein zijn ze wel aanwezig. We hebben echter niet steeds dezelfde hoeveelheid water afgewogen en zijn ook niet steeds op dezelfde starttemperatuur het afkoelen gaan meten. In feite betekent dit dat de constante K geen zuivere constante is maar deze ook een vergelijking is. Het is niet een eenvoudige relatie met massa of oppervlak van het lichaam (zie de spreadsheet afkoeling.xls). |
Conclusie:
| Een afkoelend bekerglas met water volgt exact de temperatuurwet van Newton. |
Opmerkingen:
|
Literatuur:
Relevante websites: Minder relevante websites |
Appendix:
| NQC programma gebruikt voor datalogging |
// templog.nqc // log temperature every 15 seconds for 6 hours #define SAMPLE_TIME 1500 // 15 seconds #define DATALOG_SIZE 1440 // 6 hours of data task main()
{
SetSensor(SENSOR_1, SENSOR_CELSIUS);
SelectDisplay(1);
CreateDatalog(0);
CreateDatalog(DATALOG_SIZE);
int i = 0;
while(i < DATALOG_SIZE)
{
AddToDatalog(SENSOR_1);
Wait(SAMPLE_TIME);
i++;
}
}
|
05-02-2017
dd 01072010: Niet werkende links verwijderd of aangepast.