Meten van de valversnelling

Datum: mei 2004

Principe:

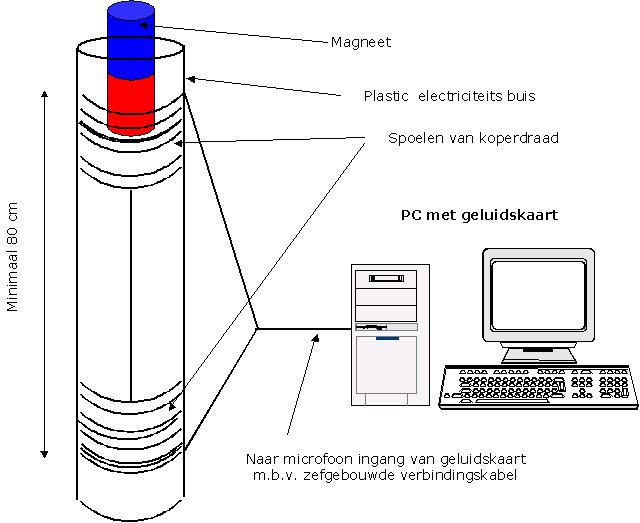
M.b.v. een magneet, enkele spoelen en een PC met geluidskaart de valversnelling meten. 

Materiaal:
  • Statief met klem
  • Staafmagneet 
  • Computer met geluidskaart
  • Microfoonkabel omgewerkt naar meetkabel
  • Meetkabels
  • Dunne koperdraad
  • elektriciteitsbuis, 1m
  • software - cool edit
    •
Uitvoering:
  • Monteer de buis verticaal zoals weergegeven op de tekening en de foto.
  • Leg een stukje piepschuim of dik zacht plastic onder de buis. 
  • Verbind de spoelen met meetkabels en de meetkabels met de speciale meetkabel die aangesloten kan worden op de ingang van de geluidskaart.
  • Start de Windows Sound recorder op. 
  • Stel deze 44.1 KHz, mono, 16 bits. Save dit format eventueel onder zijn eigen naam.
  • Start de geluidsopname.
  • Laat de magneet verschillende malen door de buis vallen.
  • Probeer er op te letten dat de onderkant van de magneet precies op een lijn ligt met de bovenkant van de buis op het moment dat je deze laat vallen.
  • Stop de opname. 
  • Save de file als een wav file
  • Lees de file in in Cool Edit
  • Analyseer het signaal. Bepaal de tijd tussen de twee pieken zoals hierbeneden weergegeven. Deze noemen we Dt.

Meetresultaten en uitwerking:
  • S1 = 8.3 cm
  • S2 = 88.6 cm
  • Massa van de magneet = 209 g

 

In dit experiment maken we gebruik van de Wet van Faraday. Een magneet die naar een spoel toe of van een spoel af beweegt, veroorzaakt een spanning over de uiteinden van de spoel: de inductiespanning. De inductiespanning over een spoel wordt veroorzaakt door een verandering van de magnetische flux M binnen de spoel. Volgens de inductiewet van Faraday is deze inductiespanning recht evenredig met het veranderingstempo van de magnetische flux binnen de spoel.

Daarom meten we de tijd op tussen de eerste spanningsverandering die we meten (de eerste piek) voor de eerste spoel en de tweede spoel.

Om de valversnelling te meten laten we een magneet door de buis vallen en bepalen de tijd die de magneet nodig heeft om zicht tussen twee punten te verplaatsen. M.b.v de formules kunnen we de versnelling van de magneet als gevolg van gravitatie berekenen. In principe hebben we maar een formule nodig nl. degene die we hierbeneden hebben afgeleid:
                                                 x = v0t + 1/2at2. 
Hierin is x de afgelegde weg, V0 de snelheid op t=0, t de tijd en a de versnelling die in dit geval gelijk is aan de gravitatieconstante.

We kunnen nu twee situaties onderscheiden, de situatie als de eerste spoel gepasseerd wordt en die waar de tweede spoel gepasseerd wordt. Verder geldt dat op t=0 v0=0. De tijd die we bepaald hebben was Dt.

De eerste spoel wordt dan gepasseerd volgens: S1 = 1/2.g.t2
De tweede spoel wordt dan gepasseerd volgens: S2 = 1/2.g.(t+Dt)2.

Je hebt nu twee vergelijkingen met twee onbekenden die je wilt oplossen voor a. Je kunt dat wiskundig netjes doen maar je kunt ook de solver (of goalseeker) van excel gebruiken  zoals ik gedaan heb. Gebruik voor Dt het gemiddelde van al je metingen.

Het resultaat van 10 metingen (in s): 
0.309 0.305 0.308 0.294 0.303 0.307 0.306 0.306 0.309 0.309
De gemiddelde van deze metingen: 0.3056 s

We berekenen dan volgens de hierboven beschreven methode een g van: 9.6 m/s2
Volgend de literatuur hebben we in Nederland een g van 9.81 m/s2.
Het verschil is tussen meting en tabelwaarde is ca. 3% relatief.

Discussie: 

Waar wordt het verschil door veroorzaakt. 
In de afleiding verwaarlozen we de wrijving die het voorwerp ondervindt, maar dit is niet de reden dat we met deze afwijking geconfronteerd worden. Het makkelijke van de gehanteerde excel-solver oplossingsmethode is dat je kunt experimenteren met de gevoeligheid van de meting. En die zit hem dus vooral in de lengtemeting. Het systeem is zeer gevoelig voor de waarde van S1. Tenzij je deze dus heel nauwkeurig kunt vastleggen en deze toestand heel goed reproduceerbaar maakt kun je een fikse afwijking van g veroorzaken. In het begin onderkende ik deze problematiek niet zo en kreeg dus waardes van 12.5 m/s2 voor g.

Conclusie:

Met dit experiment vinden we een g van 9.6 m/s2, een verschil van 3% relatief met de werkelijke waarde.

Opmerkingen:

  • In eerste instantie probeerde ik het signaal op te vangen m.b.v. oscilloscoop software. Dat wilde echter maar niet lukken met de freeware die ik tot mijn beschikking had en daarom heb ik bovenstaande constructie toegepast.
  • Een andere manier om de start conditie constant te houden is de magneet te markeren na ca. 1cm. Houd de magneet dan altijd vlak boven de markeerstreep vast. Laat je duim en wijsvinger dan de bovenkant van de magneet aanraken en laat dan los. Vergeet niet S1 en S2 voor die cm te corrigeren. 
  • Volgens de wet van Faraday is het geïnduceerde e.m.f. proportioneel met de snelheid waarmee veldlijnen verbroken worden. Aangezien dezelfde magneet door de twee spoelen valt zou het in principe mogelijk moeten zijn om te onderzoeken of het geïnduceerde e.m.f. - zoals gemeten - inderdaad proportioneel is met de snelheid van de magneet, berekend op basis van de reeds verzamelde gegevens.
    •

Literatuur:

  • Stephen Pople; "Co-ordinated Science Physics Activities"; Oxford University Press; 1989; ISBN 0199142858; p. 10, 11.
  • Ir. J.T. van Konijnenburg; "Natuurkunde zien en doen"; Agon Elsevier (Heron); 1973; ISBN 9010104354; p. 16-20.
  • R.F. Flink; "Mechanica - Natuurkunde voor het HBO"; Nijgh & Van Ditmar; 1992; ISBN 9023606744; p. 12-21.
  • Richard T. Weidner and Robert L. Sells; "Elementary Classical Physics Volume 1"; Allyn and Bacon; 1973; 2nd Ed; ISBN 0205035973;  blz. 18-32.
  • Vallen en opstaan; Archimedes; 10 (1) 1973; p. 13-19.

Relevante websites:

Minder relevante websites

Achtergrondinformatie:

Het laten vallen van een voorwerp is een fenomeen dat iedereen bekend is. We zeggen dan dat dat voorwerp door de aarde wordt aangetrokken. De aantrekkingskracht van de aarde werkt dus op dat voorwerp en deze zorgt ervoor dat een voorwerp dat eerst in rust is in beweging komt. Bepalen we nu de valtijd van een voorwerp als functie van de hoogte dan stellen we vast dat de afstand evenredig is met het kwadraat van de valtijd. Een beweging die hoort bij een afgelegde weg die evenredig is met het kwadraat van de tijd is een een eenparig veranderlijke beweging.  
Er geldt: 
Wanneer een voorwerp een versnelling of een vertraging ondergaat, dan ondervindt dit voorwerp een kracht.
Wanneer van de toestand waarin het voorwerp zicht bevindt wordt uitgegaan kan ook worden gezegd dat door de werking van een kracht de versnelling van het voorwerp van nul gaat verschillen. Met andere woorden een kracht is geen oorzaak van snelheid maar wel de oorzaak van een snelheidsverandering. Deze laatste bewering houdt in, dat elk lichaam waarop geen krachten van buitenaf werken in rust zal zijn, of een eenparige rechtlijnige beweging zal uitvoeren. Dit is een van de meest fundamentele natuurwetten, werd het eerst door Newton geformuleerd en heet daarom ook de eerste wet van Newton. Hij wordt ook wel de traagheidswet genoemd

De verplaatsing van een lichaam (massapunt) door de ruimte en door de tijd kunnen we omschrijven met de formule: x = f (t)
Deze relatie noemen we de bewegingsvergelijking van een massapunt.

De gemiddelde snelheid van een massapunt gedurende een tijdsinterval is de afgelegde weg gedurende dat tijdsinterval gemiddeld per eenheid van tijd.
In formule, met als eenheid dus m/s:

De snelheid van een massapunt bij een willekeurige rechtlijnige beweging op een tijdstip t is de grenswaarde waartoe de gemiddelde snelheid over het interval Dt, volgend op het tijdstip t, nadert als dit tijdsinterval nul nadert.
In formulevorm:

Als we nu van een willekeurige rechtlijnige beweging de snelheid v als functie van de tijd t kennen, bv v = g(t), dan kunnen we de afgelegde afstand x gedurende een tijdsinterval t door integratie oplossen:

 

De gemiddelde versnelling bij een rechtlijnige beweging van een massapunt gedurende een tijdsinterval is de snelheidstoename gedurende dat tijdsinterval gemiddeld per eenheid van tijd.

De versnelling van een massapunt bij een rechtlijnige beweging op een tijdstip t is de grenswaarde waartoe de gemiddelde versnelling over het interval Dt, volgend op het tijdstip t, nadert als dit tijdsinterval tot nul nadert. 
In formulevorm:

Als we nu der versnelling van een rechtlijnige beweging als functie van de tijd kennen (a=h(t)) dan kunnen we de snelheid berekenen:  

Omdat:

Volgt hieruit voor de snelheid v op tijdstip t:

Voor een eenparig veranderlijke rechtlijnige beweging geldt dat a constant is.

Voor de snelheid vinden we dan de vergelijking van een rechte lijn:

Voor de afgelegde weg vinden we dan de vergelijking van een parabool:  

 

Men moet zich goed realiseren dat de bovenstaande vergelijkingen betrekking hebben op het vallen in het luchtledige, als er dus geen luchtweerstand is die een remmende werking uiteoefent.

11-01-2017