Temperatuurafhankelijkheid van de weerstand van een draad

Datum: december 2002

Principe:

Door een draad aan te sluiten op een spanningsbron en deze door te meten kunnen we de invloed van de temperatuur op de weerstandswaarde bepalen.

Materiaal:

  • multimeters
  • voedingsbron of batterij
  • blokje hout
  • aansteker
  • draad, in dit geval een veer uit een goedkope balpen.
  • spijkers

Uitvoering:

  • Sla twee spijkers in het blokje hout en bevestig de draad daartussen.
  • Bouw de opstelling op volgens het schema hiernaast.
  • Sluit de spanningbron aan en meet spanning en stroom als we de draad verwarmen met de aansteker en als we de draad niet verwarmen met de aansteker.
  • Bereken de weerstand van de draad onder beide omstandigheden.


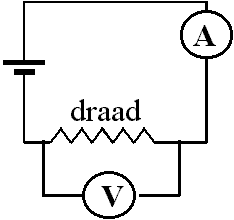
Meetresultaten:

Draad: 0.44 mm diameter                       Ingangspanning: 3 V

verwarmd U
(mV)		 I 
(mA)
nee 191 358
ja 340 332
nee 255 345
ja 384 313

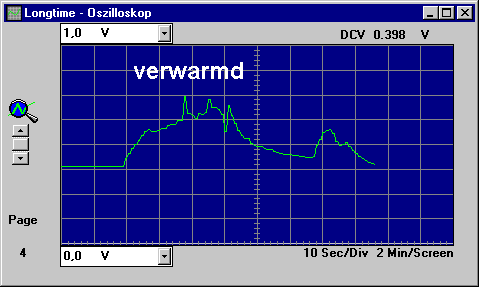
We zien dat bij het verwarmen van de draad het voltage sterk veranderd, terwijl de stroomsterkte min of meer constant blijft.

Met de wet van Ohm (U=I*R) kunnen we de weerstand van de draad berekenen.
Verwarmd 
U
 
I 
R
 
Ratio
  
(mV)
 
(mA)
 
(Ohm)
 
Rja/Rnee
nee 191 358 0.53  
ja 340 332 1.02 1.9
nee 255 345 0.74  
ja 384 313 1.22 1.6
Metalen geleiden elektriciteit aangezien de atomen in het materiaal de elektronen niet extreem sterk vasthouden waardoor vrije elektronen gecreëerd worden die een negatieve lading dragende door de draad bewegen. Weerstand wordt veroorzaakt als de elektronen die naar de + stromen als het ware over atomen heen moeten springen. Verhogen we de temperatuur van de draad dan verhogen we ook de vibratie energie (kinetische energie) van de atomen in de draad. Het gevolg daarvan is dat de kans op een botsing tussen een atoom en een elektron toeneemt. Het resultaat is een toename van de weerstand in de draad.

Conclusie:

De weerstand van een geleidende draad is afhankelijk van zijn temperatuur.

Opmerkingen:

  • Een analoog experiment hebben we uitgevoerd door het bepalen van de karakteristiek van een NTC, een weerstand met een negatieve temperatuurcoefficient: NTC karakteristiek bepalen

Literatuur:

  • IR.J.T.van Konijnenburg; "Natuurkunde Zien en Doen"; Agon Elsevier (Heron); 1973; ISBN 9010104354; blz. 85-83;94-96
  • Dr. A. Hammer; "Vademecum van de Natuurkunde"; Het Spectrum; 1964 (1979); ISBN 9027401934; blz. 69.
  • Richard T. Weidner and Robert L. Sells; "Elementary Classical Physics Volume 2"; Allyn and Bacon; 1973; 2nd Ed; ISBN 0205035981;  blz. 540-548.

Relevante websites:

Achtergrondinformatie:

De weerstand van een geleider is afhankelijk van de temperatuur. Als de temperatuur stijgt, neemt de weerstand van de meeste geleiders toe, van o.a. koolstof neemt de weerstand daarentegen af. Nadelige gevolgen hiervan zijn o.a. de grote inschakelstromen, (dit is de aanvankelijke stroomsterke) bij gloeilampen (koude gloeidraad).

Het verband dat bestaat tussen de temperatuursverandering en weerstandverandering, wordt mede bepaald door de temperatuurscoëfficiënt a, waaronder men de toe- of afname van de weerstand per Ohm per °C temperatuursverandering verstaat. De temperatuurcoëfficiënt is voor de verschillende materialen verschillend.

De weerstand van een geleider is afhankelijk van de afmetingen en van de soortelijke weerstand r volgens:

(l = lengte, A = doorsnede)

De formule geldt bij een omgevingstemperatuur van 15 °C, aangezien r opgegeven wordt bij 15 °C. Bij hogere of lagere temperaturen krijgt de weerstand een waarde die bepaald wordt door de temperatuurverandering t.o.v, 15 °C en de temperatuurscoëfficiënt van het materiaal (a).   

Voor koper is a = 0.004 (1/°C) dwz een weerstand van 1 W, vervaardigd uit koper, neemt bij een temperatuursverhoging van 15 °C tot 16 °C toe met 0.004 W zodat de weerstand 1.004 W wordt. De verandering in de weerstand ten gevolge van een temperatuursverandering is gegeven door:

(1)    DR(W) = R15(W) . a(1/°C) . DT(°C)   ==> dus de dimensie van de temperatuurcoëfficiënt is 1/°C

waarin R15 de bij 15 °C is, DT het temperatuursverschil tussen de temperatuur van de weerstand 15 °C, en a de temperatuurscoëfficiënt. De weerstand na de temperatuursverhoging wordt dus:

(2)    Rt = R15 + DR 

Hieruit volgt:

(3)     Rt = R15 + R15.a.DT = R15(1 + a.DT) = R15{1 + a.(T-15)} 

Deze formule kan gebruikt worden als de te onderzoeken weerstand inderdaad een begintemperatuur van 15 °C heeft. Is dit niet het geval dan moet de formule aangepast worden.

(4)    Rt1 = R15{1 + a.(T1-15)} 

(5)    Rt2 = R15{1 + a.(T2-15)} 

(4) + (5) ==> Rt2 / Rt1 = {1 + a.(T2-15)} / {1 + a.(T1-15)} ==> Rt2 = Rt1.[{1 + a.(T2-15)} / {1 + a.(T1-15)}]   

Voor praktisch gebruikt men de benaderingsformule:

 Rt2 = Rt1.{1 + a.(T2-T1)}   

De bovenstaande formules gelden alleen maar voor een bepaalde waarde van a alleen binnen een bepaald temperatuursgebied aangezien a slechts binnen beperkte temperatuursgebieden als constant mag worden beschouwd.

=================

De eenheid van soortelijke weerstand is 1 W .m. 
Vaak wordt de soortelijke weerstand echter in W .mm2/m opgegeven.

De reciproke waarde van de soortelijke weerstand is het soortelijk geleidingsvermogen g :

De relatieve verandering van de soortelijke weerstand (D r /r ) is evenredig met de temperatuurverandering volgens:

(a is de temperatuurcoëfficiënt van de soortelijke weerstand)


Hieruit volgt:

en:

 

08-01-2017