Videoanalyse

Datum: September 2007 - Januari 2008.

Inleiding:

Het type experimenten waarmee ik al gedurende langere tijd iets meer aan wilde doen zijn de experimenten waarbij men gebruikt maakt van videoanalyse. Een klein experiment dat ik al uitgevoerd heb op dit gebied is de "Slingerproef mbv een webcam". Dat was een eerste aanzet maar ik wilde ook graag kinematische analyses kunnen uitvoeren. Op zich is dat mogelijk met CoachLab maar jammer genoeg niet met de versie voor thuis die ik in mijn bezit heb. Ik ben daarom eens uitgebreid op het web gaan zoeken naar gratis software die beschikbaar is op dit gebied en heb inderdaad enkele gratis programma's kunnen vinden die voor dit doel geschikt zijn. Een geschikt programma is het VideoAnalyse programma dat onderdeel is van de gartis "Physics Toolkit". 

Principe:

Analyse van een vallend object.

Materiaal:

    Videocamera PC Physics Toolkit (Freeware) Videobewerkingssoftware

  • Ping pong balletje

  • Balans

  • Rolmaat

  • Schuifmaat
Deze Physics Toolkit bevat niet alleen maar een VideoAnalyse programma maar bevat ook VideoCapture software dat VFW, WDN eb DX capture devices ondersteund. Daarnaast zijn er documenten en demonstratievideo's op het gebied van natuurkunde. Het volledige pakket kan als CD gedownload worden.

Uitvoering:

  • Neem een ping pong balletje en bepaal zo nauwkeurig mogelijk de massa en de diameter.
  • Neem een dockere achtergrond en bepaal de hoogte tot een referentiepunt mbv de rolmaat
  • Laat de pingpongbal vallen en film de val en stuiterbeweging.
  • Laad de opgenomen film op de PC in een videobewerkingsprogramma en save de file  in een 320 * 288 pixel format als avi file.
  • Lees de file in in het videoanalyse deel van de Physics Toolkit en analyseer de valbeweging.

Resultaat:

Ping-pong balletje:
  • massa = 4.2 g
  • diameter = 39.73 mm
 Groter balletje:
  • massa = 9.6 g
  • diameter = 58 mm
Het resultaat kan men zien in onderstaand filmpjes.
   

YouTube link: Vallende ping pong bal

YouTube link: Vallende bal
De software kan men van de CD weer op de PC installeren en van daaruit opstarten. Dat verdient de voorkeur indien men videoanalyse wil uitvoeren. Het opent met onderstaan scherm. Klik op "Start Browser" en selecteer vervolgens "Return to videoanalysis".
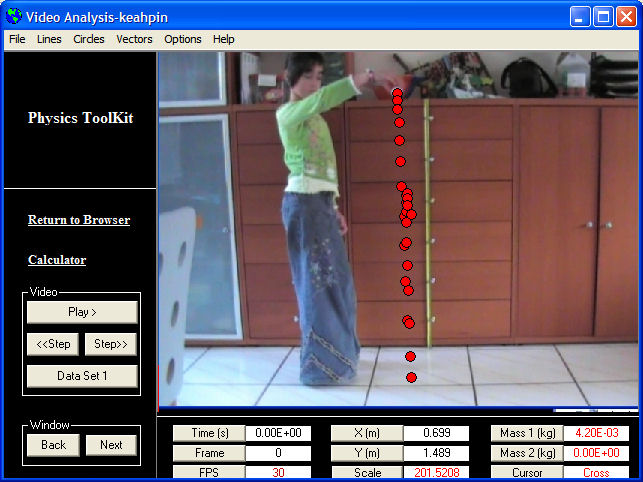
Het videoanalyse programma start op. Laad het filmpje in en volg de instructies die gegeven worden. Ga naar het  frame waar het balletje losgelaten wordt en markeer vervolgens op dit en de volgende frames de positie van het balletje. Indien het max. aantal frames is bereikt wordt dit automatisch aangegeven. Vul de massa van het balletje in en corrigeer evt. de ashoogte alsmede het aantal fps.
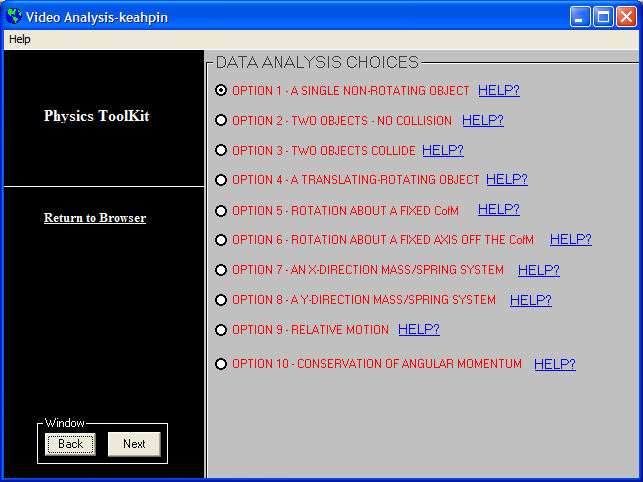
Doorloop vervolgens de daaropvolgende schermen en selecteer de benodigde opties.
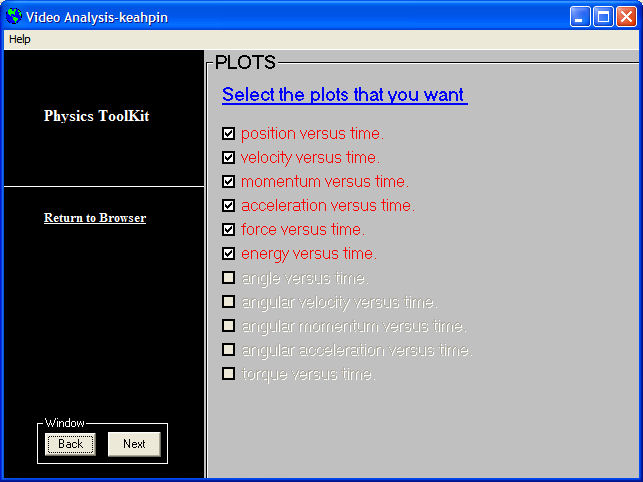
Geef in het laatste scherm aan welke data men wil analyseren.
Deze zijn vervolgens als grafiek op te vragen.

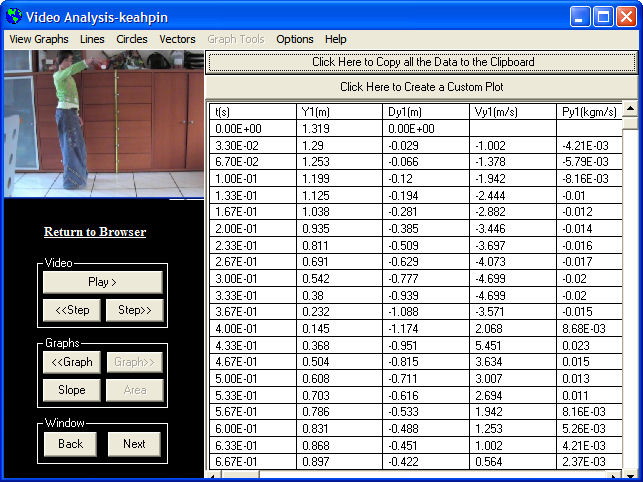
Alle data die berekend is kan opgevraagd worden en gekopieerd naar een excel sheet.
De videoanalyse heeft nu een dataset gegenereerd die we verder kunnen analyseren. Het meest interessante vindt ik altijd om te controleren of theorie en praktijk met elkaar overeen komen door een model te bouwen en dat met de meetdata te vergelijken.
 Kijken we naar de data dan kunnen we op voorhand al een conclusie trekken, nl dat ik de beginhoogte verkeerd heb ingevuld. Trekken we de hoogste en de laagste waarde van elkaar af (1.319-0.145) dan vinden we een starthoogte van 1.174 m.
Het model kunnen we globaal als volgt omschrijven:
  • De bal heeft een beginsnelheid en beginplaats (op t=0, v=0, h=1.2 m).
  • Als de bal losgelaten wordt werkt er een kracht, de zwaartekracht, op de bal.
  • Door de zwaartekracht ondervindt de bal een versnelling, en na gestuiterd te zijn een vertraging.
  • Deze vertraging/versnelling veroorzaakt een verandering van de snelheid.
  • De snelheid leidt tot verplaatsing en dus tot een verandering van de plaats van de bal

Bovenstaande zijn echter alleen maar woorden, om te kunnen rekenen hebben we formules nodig. concentreren we ons in eerste instantie op het valgedeelte dan maken we gebruik van de volgende formules:
  • Kracht of versnelling: F=m.a. of G=m.g
    Voor de zwaartekracht geldt: G=m.g
    Met m = 0.0042 kg en g = 9.81 m/s    2
  • Snelheidsverandering: v=v0 + g.t
    Met op t=0, V0=0
  • Verplaatsing: h=h0 + v0.t +1/2.g.t2
    Met op t=0, y0=1.2 m

De zwaartekracht is echter niet de enige kracht die invloed op de bal uitoefent. We hebben nl te maken met luchtweerstand. Dit betekent weer dat we met een resulterende kracht te maken hebben (zie achtergrondinformatie).

  • Luchtwrijvingskracht: Fwrijving = 1/2.Cw.(1/4.p.d2).rlucht.v2 = c.v2
    Met c= 1/2.Cw.(1/4.p.d2).rlucht
  • Resulterende kracht: FR = G - Fwrijving
  • Resulterende versnelling: a = FR/m
M.b.v. deze formules, de modelvergelijkingen, en de startwaardes kunnen we een rekenkundig model opstellen. In dit model gaan we snelheid en verplaatsing berekenen op verschillende tijdstippen. In een numeriek model maakt men voor de berekening van snelheid en plaats gebruik van een benaderingsmethode waarbij men de uitkomst van de vorige berekening gebruikt als invoer voor de nieuwe berekening. Men berekent dus in stapje (iteratief). Ook dit kunnen we in formule vorm uitdrukken volgens:
  • t = t + dt     --> verandering van het tijdstip
  • dv = a.dt     --> verandering van de snelheid per tijdstip
  • v = v + dv    --> de nieuwe snelheid
  • dh = v.dt     --> verandering van de hoogte per tijdstip
  • h = h + dh   --> nieuwe hoogte

Dit iteratieve rekenproces kunnen we ook schematisch weergeven:

Alle analyseresultaten kan men vinden in de file: dataanalyse.xls
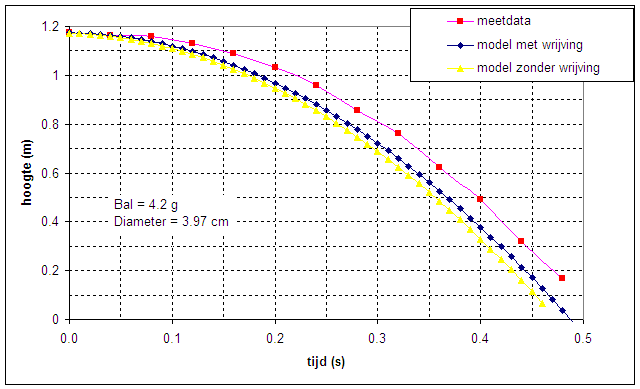
Ik heb me voor de valanalyse beperkt tot de valbeweging zelf beperkt en het stuiteren zelf buiten beschouwing gelaten.  
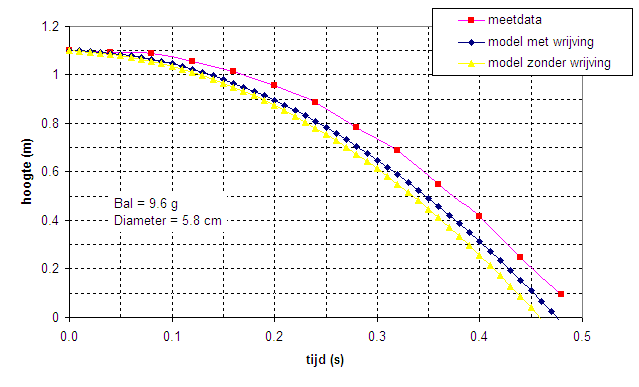
De eerste indruk die we krijgen is dat er een groot verschil is tussen theorie en werkelijkheid. Ik heb me een tijdje zitten af zitten te vragen of een en ander te maken had met het feit dat ik een ping pong balletje gebruikte dat te klein en te licht is om een merkbaar wrijvingseffect te genereren. Het experiment is daarom herhaald met een iets grotere en zwaardere balletje .
Het resultaat is weergegeven in onderstaande grafiek

Discussie en conclusie:

Met betrekking tot een eerdere opmerking van het fout invullen van de beginhoogte kan ik melden dat dat geen invoerfout was. Het programma berekent die waarde zelf en ik ben er nog niet achter hoe ik daarvoor moet corrigeren behalve dan door de correctie uit te voeren in de spreadsheet. 
Bekijken we de resultaten dan zien we dat er een verschil is tussen theorie en werkelijkheid, ervan uitgaande dat ik geen andere fouten heb zitten maken. We zien ook dat het opnemen van luchtweerstand in het model een kleine verbetering tot gevolg heeft maar nog altijd niet resulteert in een perfecte match.
Een van de dingen die je je gaat afvragen is of het programma wel de goede berekeningen uitvoert. Om dat te controleren kan men de videobeelden ook handmatig analysen door de individuele frames op te meten. Ik heb de frames van het experiment met de "grote" bal in de Excel sheet geplaatst en bij ieder frame de hoogte van het balletje opgemeten, op het scherm, mbv een liniaal (Excel op 200% gezet). Vervolgens heb ik het corresponderende tijden en hoogtes berekend. Het resultaat is weergegeven in onderstaande grafiek.

We zien onmiddellijk dat we een betere overeenkomst met de theoretische data hebben. Het lijkt nu aannemelijk om te concluderen dat het analyse programma de valbeweging niet goed modelleert, maar dat is waarschijnlijk iets te kort door de bocht geredeneerd. Waarschijnlijker is dat we met de uitvoering of data invoer een fout gemaakt hebben. Er zit me echter ook nog iets anders dwars. Ik zou verwachten dat de resultaten van mijn handmatige analyse dichter bij het model met wrijving zouden terechtkomen. Dat is echter niet het geval.  Deze observatie dwingt me om de data en de analyses te herevalueren.
Een van de dingen die ik gedaan heb is de analyse van een filmpje nogmaals uit te voeren mbv de software. Wederom wordt ik geconfronteerd met het verschil tussen de valhoogte zoals ik die invoer en degene die het programma eraan toekent (de laatste is altijd groter). Ik ben nog eens goed langs alle instellingen gelopen, heb de instructies nogmaals bekeken maar kan de verklaring hiervoor nergens vinden. Het enige dat ik kan bedenken dat er de een of ander correlatie is ingebouwd met de pixelgrootte die dit soort afwijkingen creëert. Gevoelsmatig ben ik echter geneigd om te geloven dat meetdata door het programma gegenereerd niet zover van de werkelijkheid zullen afliggen. Dat komt ook doordat de modelwaardes kleiner zijn dan de "meetwaardes". Ik zou ook verwachten dat in mijn modelberekeningen niet alle echte invloeden die op de bal uitgevoerd verdisconteerd worden. Het tegenargument is dat ik de invloeden die ik meeneem in mijn modelberekeningen ook kan overwaarderen. Ik weet gewoon niet zeker hoe dat zit. Om daar achter te komen zou ik een sensitivity analyse op het model moeten loslaten. Naast al het bovenstaande zou je eigenlijk verwachten dat de handmatige analyse de meest betrouwbare zou zijn. Kijk ik echter nog eens goed naar de handmatige analyse dan ben ik daar echter ook niet zo zeker van. Bereken ik g m.b.v. de data dan is de laagste g die ik mbv h=1/2.g.t2 bereken 10.7 m/s2. In een eerder experiment dat ik ooit eens uitgevoerd heb om de valversnelling te bepalen (valversnelling bepalen) met dezelfde formule maar met nauwkeurige tijdmeeting vond ik echter al 9.6 m/s2. Dat geeft je het idee dat de frameanalyse methode helemaal niet zo nauwkeurig is. Het is me echter een raadsel waarom. Heeft het iets te maken met de videoconversie die men moet uitvoeren?
 
Ik ben nu al enkele maanden bezig met dit experiment maar ben niet tevreden over de resultaten tot nog toe.
De enige echte conclusie die ik daarom kan trekken is dat ik dit experiment nog eens moet herhalen met een grotere bal en een betere opstelling om de opnames te maken (beeldvullend, grotere afstand, loodrecht, ...).
Misschien is het allemaal eenvoudig en zijn de fouten volledig toe te schrijven aan de videoconversies die ik uitgevoerd heb. Ook daar zal ik dus meer aandacht aan moeten besteden.

Literatuur:

  • John W. Chow, Les G. Carflton, Panteleimon Ekkakis, James G. Hay; "A Web-Based Video Digitizing System for the Study of Projectile Motion"; The Physics Teacher; 38 2000; p. 37-40.
  • M.E. Bacon, George Heal, Matt James; "A closer look at tumbling toast'; American Journal of Physics;  69 (1) 2001; p. 38-43.
  • M.E. Bacon; "How balls roll off tables'; American Journal of Physics;  73 (8) 2005; p. 722-724.
  • Robert J. Beichnter, David S. Abbott, "Video-Based Labs for Introductory Physics Courses"; Journal of Computer Science and Technology; November 1999; p. 101-104.
  • W. Bebenson and W. Bauer; "Frame grabbing techniques in undergraduate physics education"; American Journal of Physics;  61 (9) 1993; p. 848-851.
  • Priscilla Laws and Hans Pfister; "Using Digital Video Analysis in Introductory Mechanics Projects"; The Physics Teacher; 36 1998; p. 282-287.
  • William M. Wehrbein; "Using video analysis to investigate intermediate concepts in classical mechanics'; American Journal of Physics;  69 (7) 2001; p. 818-820.
  • C. de Beurs, C.H.T. Mulder; 'Fysische informatica - Vernieuwde computertoepassingen in de natuurkunde'; Thieme; 1995; ISBN 9003411085; p. 7-11,19-23.
  • 'Fysische informatica - Modelleren met de computer'; Thieme; 1995; ISBN 900341114; p. 7-14.
  • Richard T. Weidner and Robert L. Sells; "Elementary Classical Physics Volume 1"; Allyn and Bacon; 1973; 2nd Ed; ISBN 0205035973;  blz. 18-32.
  • Vallen en opstaan; Archimedes; 10 (1) 1973; p. 13-19.
  • R.F. Flink; "Mechanica - Natuurkunde voor het HBO"; Nijgh & Van Ditmar; 1992; ISBN 9023606744; p. 12-21.
  • Wilfried van Herterijck; "Gravitatie - de kracht die overal werkt"; Epsilon; 2007; ISBN 97890504110984.

Relevante websites:

Minder relevante websites:

Opmerkingen:

  • Een van de lessen die we uit dit experiment kunnen trekken is dat het belangrijk is de beginhoogte nauwkeurig te bepalen.
  • Een andere les die we kunnen trekken is dat het beter is de camera op een statief te plaatsen en van tevoren checken dat deze niet onder een hoek opneemt maar daadwerkelijk loodrecht staat.
  • Neem een grote bal voor dit soort experimenten, dat maakt de fout in plaatsbepaling en massabepaling kleiner en de bijdrage in luchtwrijving groter. Al met al kan men dan een nauwkeuriger experiment uitvoeren.
  • Het is opvallend hoeveel gegevens je over dit soort experimenten kunt vinden maar tegelijkertijd is het ontzettend lastig om meetdata en uitwerkingen te vinden.

Achtergrondinformatie:

Het laten vallen van een voorwerp is een fenomeen dat iedereen bekend is. We zeggen dan dat dat voorwerp door de aarde wordt aangetrokken. De aantrekkingskracht van de aarde werkt dus op dat voorwerp en deze zorgt ervoor dat een voorwerp dat eerst in rust is in beweging komt. Bepalen we nu de valtijd van een voorwerp als functie van de hoogte dan stellen we vast dat de afstand evenredig is met het kwadraat van de valtijd. Een beweging die hoort bij een afgelegde weg die evenredig is met het kwadraat van de tijd is een een eenparig veranderlijke beweging.  
Er geldt: 
Wanneer een voorwerp een versnelling of een vertraging ondergaat, dan ondervindt dit voorwerp een kracht.
Wanneer van de toestand waarin het voorwerp zicht bevindt wordt uitgegaan kan ook worden gezegd dat door de werking van een kracht de versnelling van het voorwerp van nul gaat verschillen. Met andere woorden een kracht is geen oorzaak van snelheid maar wel de oorzaak van een snelheidsverandering. Deze laatste bewering houdt in, dat elk lichaam waarop geen krachten van buitenaf werken in rust zal zijn, of een eenparige rechtlijnige beweging zal uitvoeren. Dit is een van de meest fundamentele natuurwetten, werd het eerst door Newton geformuleerd en heet daarom ook de eerste wet van Newton. Hij wordt ook wel de traagheidswet genoemd

De verplaatsing van een lichaam (massapunt) door de ruimte en door de tijd kunnen we omschrijven met de formule: x = f (t)
Deze relatie noemen we de bewegingsvergelijking van een massapunt.

De gemiddelde snelheid van een massapunt gedurende een tijdsinterval is de afgelegde weg gedurende dat tijdsinterval gemiddeld per eenheid van tijd.
In formule, met als eenheid dus m/s:

De snelheid van een massapunt bij een willekeurige rechtlijnige beweging op een tijdstip t is de grenswaarde waartoe de gemiddelde snelheid over het interval Dt, volgend op het tijdstip t, nadert als dit tijdsinterval nul nadert.
In formulevorm:

Als we nu van een willekeurige rechtlijnige beweging de snelheid v als functie van de tijd t kennen, bv v = g(t), dan kunnen we de afgelegde afstand x gedurende een tijdsinterval t door integratie oplossen:

 

De gemiddelde versnelling bij een rechtlijnige beweging van een massapunt gedurende een tijdsinterval is de snelheidstoename gedurende dat tijdsinterval gemiddeld per eenheid van tijd.

De versnelling van een massapunt bij een rechtlijnige beweging op een tijdstip t is de grenswaarde waartoe de gemiddelde versnelling over het interval Dt, volgend op het tijdstip t, nadert als dit tijdsinterval tot nul nadert. 
In formulevorm:

Als we nu der versnelling van een rechtlijnige beweging als functie van de tijd kennen (a=h(t)) dan kunnen we de snelheid berekenen:  

Omdat:

Volgt hieruit voor de snelheid v op tijdstip t:

Voor een eenparig veranderlijke rechtlijnige beweging geldt dat a constant is.

Voor de snelheid vinden we dan de vergelijking van een rechte lijn:

Voor de afgelegde weg vinden we dan de vergelijking van een parabool:  

 

Men moet zich goed realiseren dat de bovenstaande vergelijkingen betrekking hebben op het vallen in het luchtledige, als er dus geen luchtweerstand is die een remmende werking uiteoefent.
 

Luchtweerstand

Voor een bal bewegend door de lucht is bekend dat de luchtwrijvingskracht:
1. evenredig is met de snelheid in het kwadraat:
   Fwrijving is evenredig met v2
2. tegengesteld is aan de bewegingsrichting:
   Als v = + dan Fwrijving = - en vise versa.

Voor een beweging in de hoogte betekent dit: Fwrijving = K.v2.

K is constante die bepaald wordt door vorm en grootte van de bal:

Klucht = 1/2.Cw.A.rlucht = 1/2.Cw (1/4.p.d2).rlucht

Hierin is:

  • Cw = de luchtwrijvingscoefficient, een konstante die afhangt van de vorm van het voorwerp. Voor een bol geldt Cw = 0.45
  • r = de dichtheid van de lucht in kg/m3
  • A = het doorsnee oppervlakte van het vallende voorwerp, loodrecht op de bewegingsrichting.
  • d = diameter in m.

12/01/2017