Experimenteren met de WiiMote

Datum: December-Januari 2010

Inleiding:

Het is al weer een tijd geleden dat ik gelezen heb over de mogelijkheid om de WiiMote te gebruikten om experimenten uit te voeren. Het werd tijd om dat zelf eens te proberen.

Principe:

Gebruik maken van de sensoren die in de WiiMote verwerkt zitten om experimenten uit te voeren.

Materiaal:

  • WiiMote (+ MotionPlus)

  • Computer met Bluetooth

  • Speciale software om WiiMote te kunnen uitlezen: WiiMote Physics

  • Meetlint

  • Statief

  • Balans

Experimentele opstelling en uitvoering:

  • Als eerste moet men er zorg voor dragen dat de PC en de WiiMote met elkaar kunnen communiceren via Bluetooth.
  • Dit bereikt men door het Bluetooth programma op de laptop op te starten en het naar 'devices' te laten zoeken terwijl men tegelijkertijd de 1 en 2 knop op de WiiMote ingedrukt houdt.
  • Als het een HID device vindt vertel de software dan daar contact mee te maken. Een PIN is niet nodig voor de Wiimote, daarom kan die stap overgeslagen worden.

 

  • De default scan parameters voor de WiiMote Physics software zij weergegeven in nevenstaande figuur. Deze zijn geschikt voor het uitvoeren van de slingerproef.
  • Data acquisitie kan men starten/beëindigen via het pull-down menu "Logging" of m.b.v. CTRL F5/CTRL F6
  • Na het experiment kan me de data saven als CSV file via de pull-down menu's "File" en "Save".
  • CSV files kan importeren in Excel voor verdere analyse.

Uiteindelijk besloot ik om alleen maar een eenvoudig proof-of-principle experiment uit te voeren.
Experiment: Slingerproef
  • Bouw een statief op.
  • Bevestig de WiiMote aan het statief mbv een koord
  • Maak een Bluetooth verbdinding tussen WiiMote en PC.
  • Start de WiiMote Physics software op
  • Houdt de WiiMote een stukje omhoog met het touw strak gespannen
  • Druk op de CTRL F5 knop en laat los
  • Door na enige tijd op CTRL F6 te drukken wordt de data acquisitie gestopt.
  • Save de data file.
  • Importeer de data in Excel file en analyseer deze.

  • Het gewicht van de WiiMote + MotionPlus = 200g
  • Experiment is uitgevoerd met een  koordlengte van (inclusief WiiMote): 132 cm
  • Experiment is uitgevoerd met een starthoek van: 21 °
  • Nederland: g = 9.81 m/s2

Resultaten:

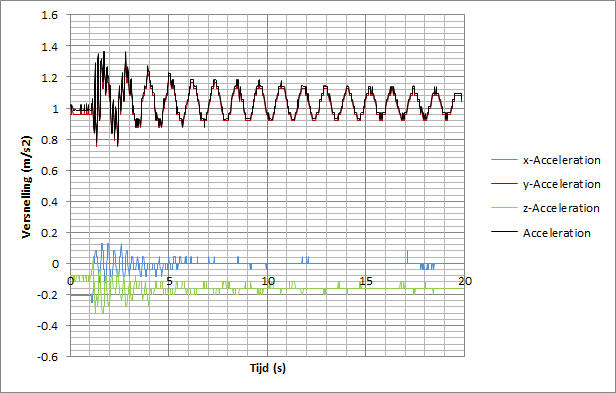
Onderstaande grafiek is een voorbeeld als degene die door de software gegenereerd wordt tijdens data acquisitie.

In de data file kan men deze data en nog wat andere data terugvinden.

 

Bovenstaande grafiek laat een mooie sinus rondom een g van ca. 1 zien. Dat liet me bedenken dat ik de slingerproef ook eens op een iets andere manier kon benaderen, n.l. of ik de lengte van het koord kon berekenen uitgaande van een bekende g m.b.v. de formule:
 
Resultaat Experiment: starthoek 21 °

--> T = 1.121 s
 Op basis van bovenstaande formule reken ik dan een koordlengte uit van 0.3 m, een afwijking van 76% t.o.v. de werkelijke waarde van 1.32 m.

Discussie en conclusie:

De WiiMote bevat een versnellingssensor waarmee de g-krachten op drie verschillende assen  gemeten kan worden, de x, y en z-as. In bovenstaande plaatje ziet men dat voornamelijk de sensor die de y-as registreert de zwaaibeweging van de slinger registreert. De kleine fluctuaties op de z-as worden veroorzaakt door het om zijn as draaien van de WiiMote.

In dit experiment hebben we alleen maar naar de versnellingssensoren gekeken. In combinatie met de IR sensor staaf die ook bij een Wii geleverd wordt kan men echter nog meer experimenten uitvoeren. De IR led's in de sensor staaf maken het in principe mogelijk om bv snelheidsmetingen uit te voeren.  Er zijn echter nog meer mogelijkheden. Enkele worden besproken in de literatuur en/of in sommige links.
Op zich heeft de data acquisitie goed gewerkt, en daar ging het primair om in dit experiment. Dat is echter een schrale troost, aangezien ik niets begrijp van het resultaat. Het enige wat ik een beetje zeker weet is dat de gemeten trillingstijd te laag is, bij deze koordlengte hadden we een trillingstijd van ca. 2 s moeten vinden en daar zijn we ver vandaan. Zoals ik al zei, momenteel begrijp ik niets van dit resultaat. Misschien een fout in de software? Dat lijkt me echter onwaarschijnlijk. Waarschijnlijker is dat ik ergens een fundamentele denkfout maak, ik zie momenteel alleen niet waar.

Literatuur:

  • Anne Schulp; 'Klussen met de Wii'; NWT; 2009 4 ; p. 78,79.
  • Raymond F. Wisman, Kyle Forinash; “Science in Your Pocket”; International Journal on Hands-on Science; 2008
  • Maurizio Vannoni, Samuele Straulino; 'Low-cost accelerometers for physics experiments';European Journal of Physics; 28 2007; p. 781–787.
  • N. Mamorita, T. Iizuka, A. Takeuchi, M. Shirataka, N. Ikeda; 'Development of a System for Measurement and Analysis of Tremor Using a Three-axis Accelerometer'; Methods of Information in Medicine; 6 2009; p. 589-594.
  • Keith Caly; 'The Pendulum, Gravity, and that Number “9.8”' ; The Physics Teacher; Vol. 42, January 2004; p. 14,15.
  • Raymond A. Serway and Jerry S. Faughn; College Physics; Thomson; 6th Ed; 2003; ISBN 0030351146; p. 402-406.
  • Niek de Kort; Klassieke Mechanica; Teleac; 1989; ISBN 9065332081; p.190-192.
  • Richard T. Weitner and Robert L. Sells; Elementary Classical Physics Volume 1; Allyn And Bacon; 2nd Ed.; 1973 (1965); ISBN 020503587; p. 270,271.

Relevante websites:

Minder relevante websites:

Opmerkingen:

  • De WiiMote kan men zich los aanschaffen in alle speelgoedwinkels en zaken die Gamecomputers verkopen voor ca. € 40.
  • Voor de Mac is het programma Darwiin Remote beschikbaar.
  • De eerste experimenten heb ik met de wii-analyzer software uitgevoerd. Deze hoeft niet geïnstalleerd te worden. Het is een stand-alone applicatie die men kan opstarten vanuit de folder waar hij deze bewaard wordt. Enige onduidelijkheid over de tijdsas heeft me er toe doen besluiten om op de WiiMote Physics sofware over te stappen.
  • De Excel files met meetresultaten is beschikbaar voor geïnteresseerden:
    slinger.xlsx

Achtergrondinformatie:

In onderstaande figuur is op een geïdealiseerde manier een eenvoudige slingerbeweging weergegeven: men puntmassa m hangt aan een massaloos koord met lengte l.

We geven de slinger een uitwijkingshoek a tov van de verticale ruststand hetgeen betekent dat de massa een booglengte aL van de evenwichtspositie afraakt. De zwaartekracht zorgt er nu voor dat deze massa weer terugkeert naar de evenwichtspositie.  De kracht die uitgeoefend wordt kunnen we ontleden in twee componenten waarvan er een loodrecht op het koord staat, de grootte van die kracht is -mg.sina. De versnelling van de afgelegde weg is gelijk aan de 2de afgeleide van de verplaatste booglengte. 

Langs de boog gezien geldt de 2de wet van Newton: ma=F, dus:


Deze vergelijking is niet de vergelijking voor een eenvoudige harmonische beweging. De 2de afgeleiden van de verplaatsing (de hoek a) is niet evenredig met –a maar met –sina.

De hierboven afgeleide dv kent geen eenvoudige oplossing maar door gebruik te maken dat voor kleine hoeken van a geldt dat deze gelijk is aan de sinus kunnen we hem hanteerbaarder maken.

Indien a dusdanig klein is dat sina ~a geldt:

Dit is de algemene dv voor een harmonische oscillator met als  oplossing:

 

Waarbij a0 de uitwijking is die bij de start geldt.
Voor de hoekfrequentie geldt:

Waardoor voor de trillingstijd geldt dat:  

De slingertijd wordt dus bepaald door de lengte van het koord aangezien g op aarde nagenoeg constant is.

De slingertijd is de tijdsduur die verloopt tussen twee momenten waarop een punt (bijvoorbeeld de massa) van een slinger zich weer op hetzelfde uiteinde bevindt. 

De slingertijd wordt ook wel periode genoemd.

Uit de formule van de slingertijd kunnen we afleiden dat de periode van een slinger alleen maar afhankelijk is van de lengte van de slinger en de gravitatieconstante. Ook speelt de amplitudo niet een bijzonder grote rol zolang deze relatief klein is (sinusbenadering moet blijven gelden). Deze afhankelijkheid maakt het mogelijk de slinger als klok te gebruiken. 

Galileo was de eerste die opmerkte dat de periode van een slinger onafhankelijk is van zijn amplitudo. 

Geologen maken gebruik van een slinger als ze op zoek zijn naar olie en mineralen. Afzetting beneden het oppervlak van de aarde kunnen afwijkingen in de gravitatieconstante veroorzaken. Door gebruik te maken van een speciaal ontworpen slinger van bekende lengte wordt de periode gemeten, die dan weer gebruikt wordt om g te berekenen
 
Screenshot met wii_analyzer software

17/01/2017