Het geluid van een klappende zeepbel

Datum: September 2006

Principe:

Met microfoons, PC en software bepalen of een zeepbel geluid maakt als deze klapt.

Inleiding:

Op zaterdag 26 augustus zat ik in de wetenschapsbijlage een stukje van Theo Jansen te lezen over bellen blazen.  In dat stukje beweerde hij dat "bij het ontploffen van  een zeepbel ontstaat onhoorbaar geluid". Ik dacht eigenlijk onmiddellijk dat die bewering niet klopte. Volgens mij kun je soms horen dat een geluidsbel een plof geluid maakt als hij klapt. Denken is een ding maar een meer wetenschappelijke vraag is of ik dat ook kan meten. Om die vraag te beantwoorden heb ik onderstaande experimenten uitgevoerd.

Materiaal:

PC benadering
  • PC
  • Microfoon
  • Software pakket: Audacity
    (Audacity is gratis, open source software voor het opnemen en bewerken van geluid).
 Coachlab benadering
  • Coachlab II met PC
  • Geluidssensor (017i)
Verder nog:
  • bellenblazer (neem wat draad en buig er een oogje op)
  • Voor dit experiment heb ik het zeepsop recept gebruikt waarmee men grote bellen kan maken:
    Los 500 g suiker in 1 liter warm water. Meng vervolgens 750 ml afwasmiddel met 1 liter water. Meng 60 ml glycerine en 5 l water door elkaar. Meng de drie oplossingen goed door elkaar. Laat het mengsel voor gebruik minimaal enkele uren staan.

Uitvoering:

De uitvoering is eenvoudig. Blaas een zeepbel door de bellenblazer, vang deze op, houdt de bel zo dicht als maar mogelijk is bij de sensor of microfoon, start de meting/opname en laat de bel klappen.
 Coachlab metingen


De meetresultaten zijn opgeslagen in de file: overzichtcoachlab.xls

 
PC met microfoon - screenshot van Audicity na een opname.
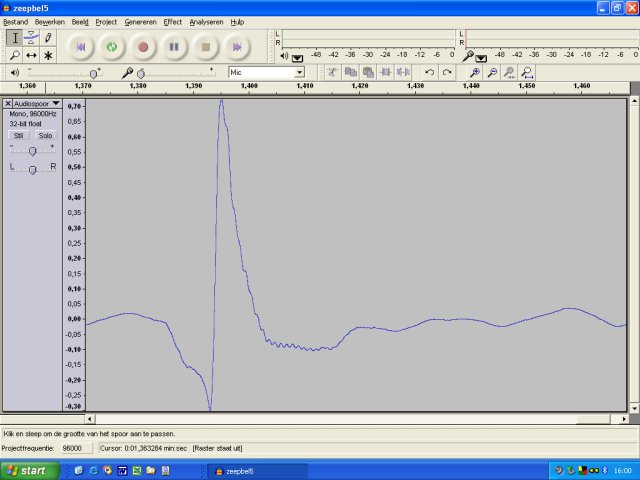De meetinstellingen waren vnl Mono, 44000 Hz. In het experiment hierboven weergegeven werd 96000 Hz gebruikt. Een viertal meting zijn uitgevoerd, geanalyseerd mbv audicity en de resulaten opgeslagen als WAV file.

Meetresultaten en uitwerking:

Een van de waarnemingen die gedaan werd tijdens de uitvoering van deze experimenten is dat zeepbellen inderdaad geluid maken als ze ploffen. Dat kun je gewoon horen.

Coachlab
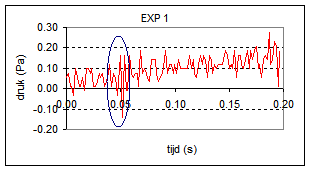
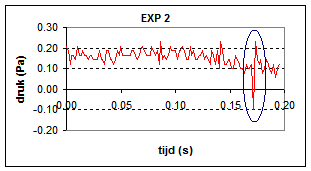
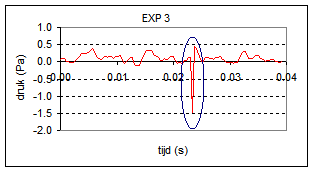
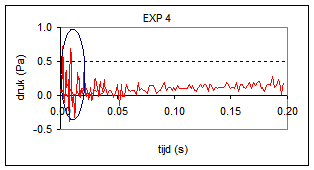
De sensor bevat een microfoon met een interne versterker. Vanwege de grote gevoeligheid is de sensor ook geschikt om kortdurende drukpulsen (bv. stuiterend balletje) te detecteren. Deze sensor is lineair over zijn gehele meetbereik. Meetbereik: -45..45 Pa. Uiteindelijk heb ik een vijftal metingen uitgevoerd die weergegeven worden in onderstaande grafieken.
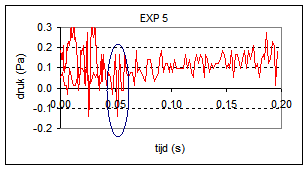De coachlab metingen laten zien dat het geluid van een ploffende zeepbel gepaard gaat met een drukpuls in de range 0.2 - 1.5 Pa, een zeer klein drukverschil maar wel meetbaar. Exp 4 is twijfelachtig, mogelijk dat wat achtergrondgeluid het signaal vertroebelt.

PC met microfoon
We kunnen een geluidsfragment afspelen door op onderstaande link te drukken. Het geluid is zeer zacht, om het goed te kunnen horen moet men de volumeknop hoogdraaien.

1. zeepbel1.wav  --> 0.4 dB
2. zeepbel2.wav  --> -0.5 dB
3. zeepbel3.wav --> 1 dB
4. zeepbel4.wav -- > 1 dB (top-top)

In bovenstaande meting kunnen we ook zien dat we voor de klappende bel een geluidssterkte in de range van 0.4 - 1 dB meten mbv een PC microfoon.

Discussie:

Ook na aardig wat literatuuronderzoek gedaan te hebben heb ik geen echte referentie kunnen vinden die verwijst naar het geluid dat een zeepbel maakt Indien men in de literatuur gaat spitten komt men eigenlijk geen referentie vinden, ook in het boek van Boys niet. Het boek van Hildebrand behandeld een zeepbel vnl als een minimaaloppervlak maar gaat slechts zeer summier in op de fysische achtergrond. Ook in het artikel van Goran Ramme, die onderzoek heeft gedaan naar de spatpatronen die ontstaan bij het klappen van zeepbellen, vermeld niet of een klappende zeepbel met geluid gepaard gaat. Hij spreekt echter wel van explosies, hetgeen in ieder geval die suggestie geeft dat klappen met geluid gepaard gaat.

Alhoewel we nu experimenteel hebben vastgesteld dat er geluid ontstaat bij het ploffen van een zeepbel hebben we nog niet bediscussieerd waar dat geluid vandaan komt. In de achtergrondinformatie wordt ingegaan op de wet van Laplace-Young waarmee de vorm van een zeepbel afgeleid is. De formule laat zien dat er een relatie is tussen de druk in de zeepbel, de omgevingsdruk en de oppervlaktespanning. Het komt erop neer dat de druk binnen een zeepbel iets hoger is dan de omgevingsdruk. Bij het klappen van de zeepbel ontstaat er dus een drukpuls en een drukpuls is in feite synoniem met geluid. Op hoge snelheids foto's van een klappende zeepbel die ik wel eens gezien heb zie ik je relatief grote lappen van de zeepoplossing slingeren. Dat slingeren kan mogelijk ook leiden tot luchttrillingen die weer een bijdrage leveren aan het geluid dat we horen. Hierbij moet aangetekend worden dat de metingen met de Coachlab suggereren dat we maar met een enkele puls te maken hebben. Ik ben me echter niet zeker of dergelijke metingen dermate nauwkeurig zijn dat we zulk een kleine bijdrage zouden kunnen waarnemen.

Er is nog iets anders aan de hand met de Coachlab metingen, we zien nl in 4 van de 5 metingen een negatieve piek. Gevoelsmatig zou ik zeggen dat dat het signaal van een implosie is, niet een explosie. Dat zou echter suggereren dat we met een onderdruk te maken hebben in de zeepbel hetgeen niet in overeenstemming is met de Wet van Laplace-Young. Ik moet echter ook opmerken dat ik geen specialist ben in het interpreteren van dergelijke geluidssignalen dus misschien is er wel een andere, meer plausibeler verklaring.
  

Met de wet van Laplace-Young kunnen we ook de druk binnen een bel uitrekenen volgens (zie achtergrondinformatie):

Door nu deze formule te gebruiken om de druk uit te rekenen voor bellen van water (0.073 N/m bij 20 oC), glycerine (0.063 N/m)  en zeepoplossingen waarvoor Roman et al de oppervlaktespanning bepaald hebben (0.021 en 0.024 N/m) kunnen we de volgende grafiek maken.

Door zeep aan een oplossing toe te voegen verlagen we de oppervlaktespanning hetgeen lijdt tot een lagere interne druk binnen een zeepbel. We zien dat bij een grotere straal de berekende druk al aardig in de buurt komt van de met Coachlab gemeten waarden. Ik heb indertijd niet de diameter van de zeepbellen gemeten maar kijken we naar de foto's hierboven dan lijkt het erop dat de straal van de zeepbel overeenkomt met een microfoonkop, die ca 4 cm lang is. De berekende druk voor een zeepbel is dan ca. 2 Pa. Daarnaast is het zo dat Roman et al alleen van een waterige zeepoplossing de oppervlaktespanning bepaald hebben. De in deze experimenten gebruikte zeepoplossing bevat echter ook glycerine, dat een lagere oppervlaktespanning heeft dan water. Het is dus aannemelijk dat de in dit experiment gebruikte zeepoplossing ook een lagere oppervlaktespanning zal hebben waardoor de druk nog iets lager zal uitvallen en nog dichter in de buurt van de gemeten waarde zal komen.
De metingen met de PC geven aan de de geluidssterkte van een ploffende zeepbel ca. 0.4-1 dB is. Nu is er echter een rechtstreekse relatie tussen geluidssterkte en druk (zie de onderstaande Wikipedia link). Ik dacht dat ik daar mogelijkerwijs ook de druk in de zeepbel mee kon uitrekenen volgens (hierin is p0 de referentiedruk van 20 uPa, de onderste gehoorgrens):
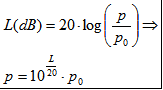Met deze formule en een geluidssterkte van 1 dB berekenen we een druk van slechts 2.24.10-5 Pa, veel lager dan de sensormetingen aangeven.
Waarom deze berekening een druk geeft die veel lager is dan met Coachlab gemeten is me niet helemaal duidelijk. Waarschijnlijk heeft de bouw van de microfoon er iets mee te maken heeft. Wanneer iemand in een microfoon spreekt, dan komt er ook uitgeblazen lucht mee. Dat geeft een hard klapperend windgeluid op de microfoon. De meeste microfoons, en vooral electret microfoon zijn daar erg gevoelig voor. Door gebruik te maken van een plopkapje wordt dat voorkomen. Een plopkapje een meestal een omhulsel van schuim (bijvoorbeeld polyetherschuim). Als een dergelijke constructie in de PC microfoon verwerkt zit dan zou dat tot signaaldemping kunnen leiden en zo de veel lagere waarde kunnen verklaren.

Conclusie:

  • In tegenstelling tot de bewering van de journalist maken zeepbellen wel degelijk geluid als ze klappen.

Opmerkingen:

  • Ik heb laatst, alhoewel het nazomer is, een bellenblaas en zeepoplossing zoals ze die in de speelgoedwinkel verkopen kunnen verwerven. De zeep daarin is veel lichter dan de in dit experiment gebruikte en maakt veel minder geluid als de bel klapt. 

  • De kleur van een zeepbel is een indicatie voor de dikte van de wand. De kleur ontstaat door interferentie.

Literatuur:

  • Column Theo Janssen; Volkskrant; 26 augustus 2006

  • CV Boys; 'Soap-Bubbles - their colours and the forces which mold them'; Dover; 1959 (1911); ISBN 0486205428.

  • Stefan Hildebrand en Anthony Tromba; 'Architectuur in de Natuur - De weg naar de optimale vorm'; Natuur&Techniek; 1989 (1985); ISBN 9070157810; p. 91-143.

  • Goran Ramme; "The bubble bursts"; Physics Education; 24 1989; p. 147-154.

  • F.L. Roman, J. Faro, S. Velasco; "A simple experiment for measuring the surface tension of soap solutions"; American Journal of Physics; 69 8 2001; p. 920, 921.

Relevante websites:

Achtergrondinformatie:

Als men over zeepbellen praat dan praat men eigenlijk ook over oppervlaktespanning. Oppervlaktespanning kan men definiëren als het virtuele "membraan" dat ontstaat op elk grensvlak tussen gas en vloeistof. Moleculen die zich vrij in een oplossing kunnen voortbewegen ondervinden gemiddeld gesproken dezelfde krachten vanuit alle richtingen uitgeoefend door de moleculen in hun omgeving.

In het bovenste laagje van de vloeistof, de grenslaag tussen vloeistof en gas zullen de vloeistofmoleculen onder die laag zullen sterker aan deze moleculen trekken dan de gasmoleculen die erboven zitten. Het gevolg daarvan is dat de moleculen die in dat bovenste laagje zitten de neiging zullen hebben om de grenslaag te verlaten om naar de bulk te bewegen. Deze voorkeursrichting van de moleculen zorgt ervoor dat het oppervlak krimpt tot het kleinst mogelijke oppervlakte (vandaar de vorm van een waterdruppel).

Oppervlaktespanning zorgt ervoor dat een zeepbel een ronde vorm krijgt omdat dat het kleinst mogelijk oppervlak is. In het begin van de 19de eeuw hebben Thomas Young en Pierre Simon Laplace onafhankelijk van elkaar een vergelijking afgeleid die men de wet van Young Laplace noemt:
Druk = (2 * oppervlaktespanning(g))/(straal(r) van het oppervlak)
De druk verwijst in dit geval naar het verschil in druk van het binnenste van een vloeistofdruppel vergeleken met de druk buiten de druppel. De grootte van dit drukverschil wordt bepaald door twee factoren: grootte van de druppel en oppervlaktespanning. Des te kleiner de druppel des te groter de druk binnen de druppel.

Zeep in een waterige oplossing reduceert de oppervlaktespanning. In een zeepbel is een wet analoog aan die van Laplace-Young van toepassing. Door de verlaging van de oppervlaktespanning wordt het drukverschil tussen de binnenkant en de buitenkant van de zeepbel ook kleiner totdat er een evenwicht gevormd is dat pas verbroken wordt als de bel begint te drogen en de waterfilm dun genoeg wordt om te breken. Bij een te hoge oppervlaktespanning zou het drukverschil tussen binnen en buitenkant van de bel darmate groot zijn dat de bel niet zijn bolvorm zou kunnen behouden en in elkaar zou storten.

 
Afleiding van de Laplace Young vergelijking.

Als we het oppervlak van een film willen vergroten moeten we een kracht F uitoefenen. Als dat oppervlak een breedte b heeft dan is de kracht die we moeten uitoefenen evenredig aan b.

Hierin is g de oppervlaktespanning. De hoeveelheid arbeid die we dan verrichten is:

Hierin is A de oppervlaktevergroting. Als de verrichte arbeid reversibel is dan is de hoeveelheid gelijk aan de verandering in Gibbs energie:

 

Hetgeen we weer kunnen gebruiken om de oppervlaktespanning te definieren als:

Hetgeen we kunnen omvormen tot:

Het is van belang zich te realiseren dat we bij een film niet te maken hebben met een oppervlak maar met 2 oppervlakken:

Voor een systeem in een mechanisch evenwicht geldt:

Kijken we alleen naar de bulk dan geldt:

Aangezien:

Dan is:

Als we nu het interface ook in de vergelijking opnemen dan nemen we de verandering in interne energie t.g.v. het oppervlak mee:

We krijgen dan:

Dus:

Deze vergelijking laat zien dat er een drukverschil is tussen de twee gebieden waar een film mee te maken heeft als deze van volume veranderd (bv binnen- en buitenkant). Deze vergelijking noemt men de Laplace Young vergelijking.

Voor een bolvormige druppel:

Dan wordt:

Dus voor een vloeistofdruppel:

We kunnen deze vergelijking ook anders afleiden.

De kracht die inwendig gericht is ten gevolge van de oppervlaktespanning is:

De kracht die uitwendig gericht is tgv het drukverschil is:

Bij een systeem in evenwicht is de nettokracht 0:

Voor een bolvormige zeepbel geldt dat we een binnen en een buiten interface hetgeen resulteert in:

 

13-01-2017