De slingerproef mbv CoachLab

Datum: april 2006

Principe:

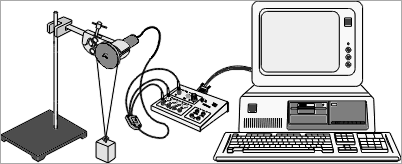
M.b.v. een slinger, een draaihoeksensor en CoachLab voeren we de slingerproef uit waaruit we dan de waarde van g bepalen.

Materiaal:

  • Coachlab II met
      Draaihoeksensor (B031)
  • Statief
  • Draad (verschillende lengtes) 
  • Gewichten (50 g, 70 g, 100 g)

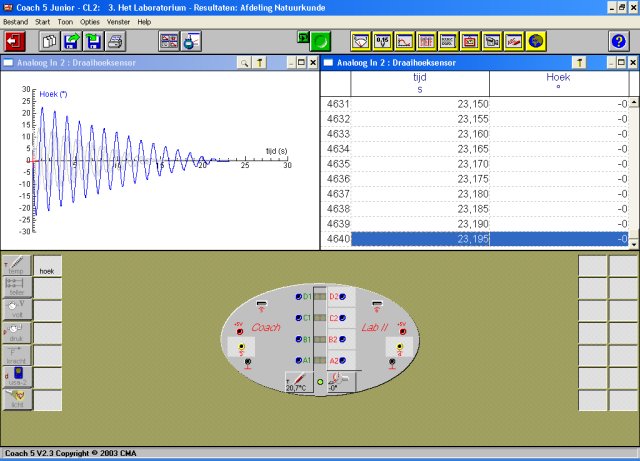
Uitvoering:

  • Bouw de opstelling op zoals hiernaast en hierboven is weergegeven.

  • Activeer het Coachlab programma, selecteer de draaihoeksensor en pas tabellen en grafieken aan zoals hierbeneden is weergegeven.

 Bron: CMA
  • Positioneer de sensor dusdanig dat de waarde 00 aangeeft.
  • Ga vervolgens metingen uitvoeren met verschillende koordlengtes, gewichten en starthoeken.
  • Sla elke meting op als een dif file die men in excel kan inlezen.
  • Voor de data-analyse en het samenvoegen van de resultaten heb ik een aparte spreadsheet gemaakt met daarin een macro die het makkelijker maakt om de trillingstijd te bepalen. 
  • Door op de knop "opschonen" te drukken wordt de kolom leeggemaakt.
  • Open een dif file met daarin de resultaten van een meting en kopieer de kolommen als "value" in de bewerkingssheet. 
  • Druk vervolgens op de knop "analyseer data" en controleer vervolgens de trillingstijden.
  • Verwijder op het einde de afwijkende metingen. De fout wordt daar te groot.
  • Kopieer de gevonden trillingstijd en het aantal metingen waarop deze gebaseerd is naar de verzamelsheet. 

Meetresultaten en uitwerking:

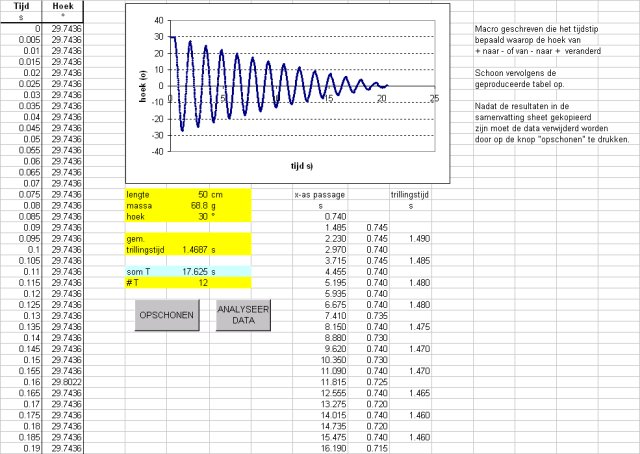
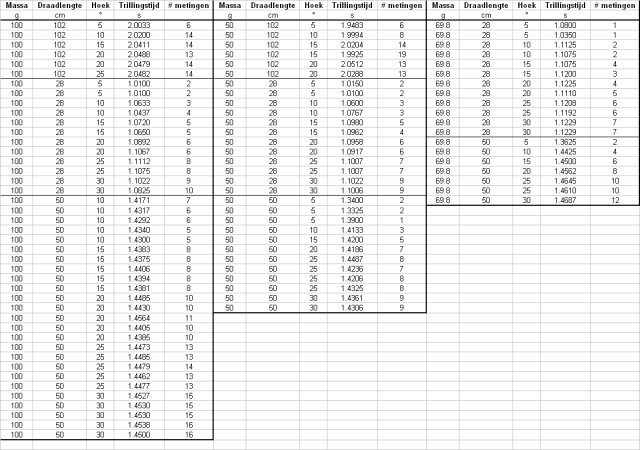
De resultaten zijn verzameld in de sheet: resultaten.xls
De verkregen meetwaardes zijn weergegeven in onderstaand tabel.

Discussie: 
We kunnen de verkregen resultaten ook grafisch uitzetten zoals gedaan in onderstaande grafiek. Zonder naar de mathematisch vergelijkingen te kijken kunnen we dan al een aantal conclusies trekken over de slingertijd.
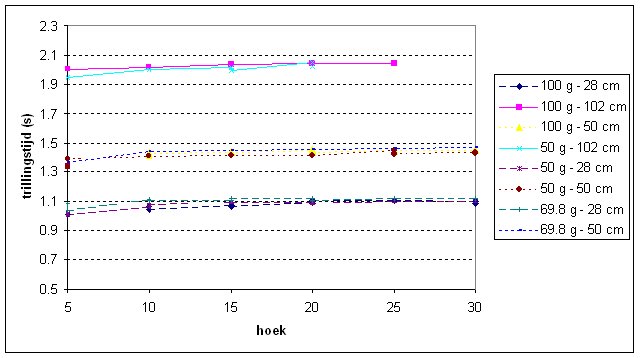We kunnen aan de grafiek zien dat de slingertijd is onafhankelijk van zowel "starthoek" als van gewicht.
Plotten we vervolgens de slingertijd als functie van de koordlengte dan krijgen we onderstaande grafiek.
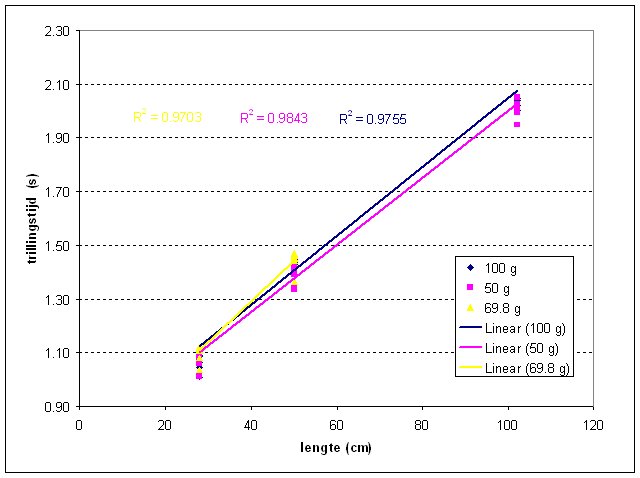Uit deze grafiek kunnen we aflezen dat er een lineaire relatie is tussen de koordlengte en de slingertijd en dat deze ook deze relatie onafhankelijk is van het gewicht.
Een andere manier om naar de resultaten te kijken is door de gravitatieconstante te berekenen volgens onderstaande formule die in "achtergrondinformatie" is afgeleid.
We kunnen g zelfs uitrekenen als een gewogen gemiddelde door het aantal trillingen dat we in een meting hebben gebruikt in de berekening te verwerken. De op deze manier gevonden g = 9.49 m/s2. Volgens de handboeken mogen we een waarde van 9.81 m/s2 verwachten. De afwijking tussen meetwaarde en de "echte" waarde is 3% relatief. Op zich is dat niet zo groot alhoewel ik, gezien het groot aantal metingen (711) dat hierin verwerkt, zit een kleinere afwijking verwacht had. Het is me niet helemaal duidelijk waardoor de afwijking veroorzaakt wordt. 

Conclusie:

  • De slingertijd is onafhankelijk van de slingerhoek als van het gewicht dat aan de slinger hangt.
  • Er is een lineaire relatie tussen de koordlengte van de slinger en de slingertijd die ook weer onafhankelijk is van gewicht en starthoek.

Literatuur:

  • T.H. Savory; Natuurkunde Thuis; Thieme; 2de druk; p. 25-30.
  • Keith Caly; 'The Pendulum, Gravity, and that Number “9.8”' ; The Physics Teacher; Vol. 42, January 2004; p. 14,15.
  • Dr. J. Schweers en Drs. P. van Vianen; Natuurkunde op copusculaire grondslag - Deel drie voor de bovenbouw van het vhmo; Malmberg; 12de druk; 1964; p.1986, 1987. 
  • Raymond A. Serway and Jerry S. Faughn; College Physics; Thomson; 6th Ed; 2003; ISBN 0030351146; p. 402-406.
  • Niek de Kort; Klassieke Mechanica; Teleac; 1989; ISBN 9065332081; p.190-192.
  • Richard T. Weitner and Robert L. Sells; Elementary Classical Physics Volume 1; Allyn And Bacon; 2nd Ed.; 1973 (1965); ISBN 020503587; p. 270,271. 

Achtergrondinformatie:

In onderstaande figuur is op een geïdealiseerde manier een eenvoudige slingerbeweging weergegeven: men puntmassa m hangt aan een massaloos koord met lengte l.

We geven de slinger een uitwijkingshoek a tov van de verticale ruststand hetgeen betekent dat de massa een booglengte aL van de evenwichtspositie afraakt. De zwaartekracht zorgt er nu voor dat deze massa weer terugkeert naar de evenwichtspositie.  De kracht die uitgeoefend wordt kunnen we ontleden in twee componenten waarvan er een loodrecht op het koord staat, de grootte van die kracht is -mg.sina. De versnelling van de afgelegde weg is gelijk aan de 2de afgeleide van de verplaatste booglengte. 

Langs de boog gezien geldt de 2de wet van Newton: ma=F, dus:


Deze vergelijking is niet de vergelijking voor een eenvoudige harmonische beweging. De 2de afgeleiden van de verplaatsing (de hoek a) is niet evenredig met –a maar met –sina.

De hierboven afgeleide dv kent geen eenvoudige oplossing maar door gebruik te maken dat voor kleine hoeken van a geldt dat deze gelijk is aan de sinus kunnen we hem hanteerbaarder maken.

Indien a dusdanig klein is dat sina ~a geldt:

Dit is de algemene dv voor een harmonische oscillator met als  oplossing:

 

Waarbij a0 de uitwijking is die bij de start geldt.
Voor de hoekfrequentie geldt:

Waardoor voor de trillingstijd geldt dat:  

De slingertijd wordt dus bepaald door de lengte van het koord aangezien g op aarde nagenoeg constant is.

De slingertijd is de tijdsduur die verloopt tussen twee momenten waarop een punt (bijvoorbeeld de massa) van een slinger zich weer op hetzelfde uiteinde bevindt. 

De slingertijd wordt ook wel periode genoemd.

Uit de formule van de slingertijd kunnen we afleiden dat de periode van een slinger alleen maar afhankelijk is van de lengte van de slinger en de gravitatieconstante. Ook speelt de amplitudo niet een bijzonder grote rol zolang deze relatief klein is (sinusbenadering moet blijven gelden). Deze afhankelijkheid maakt het mogelijk de slinger als klok te gebruiken. 

Galileo was de eerste die opmerkte dat de periode van een slinger onafhankelijk is van zijn amplitudo. 

Geologen maken gebruik van een slinger als ze op zoek zijn naar olie en mineralen. Afzetting beneden het oppervlak van de aarde kunnen afwijkingen in de gravitatieconstante veroorzaken. Door gebruik te maken van een speciaal ontworpen slinger van bekende lengte wordt de periode gemeten, die dan weer gebruikt wordt om g te berekenen

17-01-2017