

| Potentiometrische titratie van cola |  |
 |
Datum : januari 2004
Principe:
| Ooit heb ik ergens gelezen dat er fosforzuur in
cola zit. Met behulp van potentiometrische titraties probeer ik dat te
onderzoeken.
Het gehalte van fosforzuur (H3PO4) bepalen d.m.v.
een zuur-base reactie met natronloog. |
Benodigd:
|
Fosforzuur (80%) |
|
Werkwijze:
Bereiding van de 0.05 m loogoplossing.
|
|
Titratie van cola (zonder CO2)
| |
Titratie van cola (met CO2)
Titratie van fosforzuur
| |
Meetresultaten en resultaten:
|
De in dit experiment gebruikte pH meter is aan een computer gekoppeld waardoor we de beschikking hebben over software die het leven iets gemakkelijker maakt. |
|
|
|
De meetresultaten kunnen we nu rechtstreeks
exporteren als tekstfile en importeren in excel
om verder te bewerken en zo onderstaande titratiecurve af te leiden. De
concentratie van de NaOH oplossing was 0.05 M hetgeen betekent dat 1ml NaOH
opl. = 0.05 mmol NaOH (0.05 mol/l = 0.05 mmol/ml). Alle directe meetresultaten zijn samengevoegd in onderstaande grafiek. Alle metingen en berekeningen zijn te vinden in een downloadbare excel file. |
|
|
|
Het equivalentiepunt vinden we in de
titratiecurve terug als een buigpunt. Voor een buigpunt in een curve geldt
dat de 1ste afgeleide een maximum moet vertonen, terwijl de 2de afgeleide
daar de waarde nul moet hebben. Deze afgeleiden of differentiaalquotiŽnten
kunnen worden benaderd door differentiequotiŽnten. Omdat extrapoleren
naar een maximum nogal lastig is, bepaalt men ook het tweede differentiequotiŽnt
pH", waarvoor geldt: pH"= d2pH/dmmol2=D2pH=Dml2. Een equivalentiepunt ligt dan bv bij: 4.5 * ((1.3/(1.3+0.8))*0.5) * 0.05 = 0.240 mmol NaOH Zie onderstaande tabel voor de resultaten. |
|
|
Zoals hierboven weergegeven hebben we nu
voldoend gegevens om de concentratieberekeningen uit te voeren. Als
voorbeeld de H3PO4 titratie (molmassa H3PO4
= (3*1+31+4*16) = 98 g/mol). Om 1 mmol H3PO4 volledig te neutraliseren heb ik 3 mmol NaOH nodig. Dit betekent echter ook dat ik 3 equivalentiepunten zou moeten zien. We zien er echter maar 2 hetgeen impliceert: 2NaOH + H3PO4 --> 2H2O + 2Na+ + HPO42- Gebruikt 0.6 mmol NaOH = 0.6/2 = 0.3 mmol H3PO4. Het volume van de oplossing was ca. 50 ml. Concentratie H3PO4 = 0.3/50 = 0.006 mmol/ml = 0.006 mol/l = 0.006 *98/10 g/100 ml = 0.06 % H3PO4 |
Discussie:
| Om op de vraag of er fosforzuur in cola zit te beantwoorden
kun je natuurlijk eerst eens op het etiket kijken. Het staat er niet zo
duidelijk op maar wel wordt een range van voedingszuren vermeld nl.
e338-e330. Met wat zoeken op het web blijkt dat met voedingszuur e338
fosforzuur bedoeld wordt. Voedingszuren worden aan voedsel toegevoegd
omdat ze de zuurgraad verhogen en bacteriŽn en gisten
tegenwerken. Bovendien geeft het een fris-zure smaak.
Het experiment met de cola die enige tijd had gestaan werd ingevoerd omdat op voorhand al werd vermoed dat de CO2 in de cola wel eens invloed zou kunnen uitoefenen op de titratie. Een vermoeden dat bevestigd werd. De titratie met H3PO4 hebben we uitgevoerd om als referentie te dienen. Ook is te zien aan de titratiecurve van het H3PO4 en de oude cola dat deze niet identiek van vorm zijn. Dat is niet zo verwonderlijk aangezien uit het etiket al blijkt dat cola vele ingrediŽnten bevat. In het geval van anorganische en organische zouten aan een bufferend effect kunnen meewerken. Daarnaast kunnen de andere aanwezige voedingszuren een rol hebben. |
|
| Uiteraard is dit niet een zeer nauwkeurige analysemethode, de loog is bv niet gesteld waardoor de concentratie kan afwijken van hetgeen we op basis van de weegcijfers verwachten. We weten bv dat loog reageert met het water en CO2 uit de lucht. Zie de opmerkingen hierbeneden. | |
| De afleidingen voor de pH
berekeningen en titratiecurves staan hierbeneden uitgewerkt in
achtergrondinformatie en kan men ook bekijken als word
document. De uitwerkingen zijn gedaan in een excel spreadsheet die ook opgehaald kan worden. Hierin staat ook vermeld waarom we maar 2 equivalentiepunten waarnemen. De autoprotolyse van water domineert in het gebied waar het derde equivalentiepunt zou moeten plaatsvinden. |
|
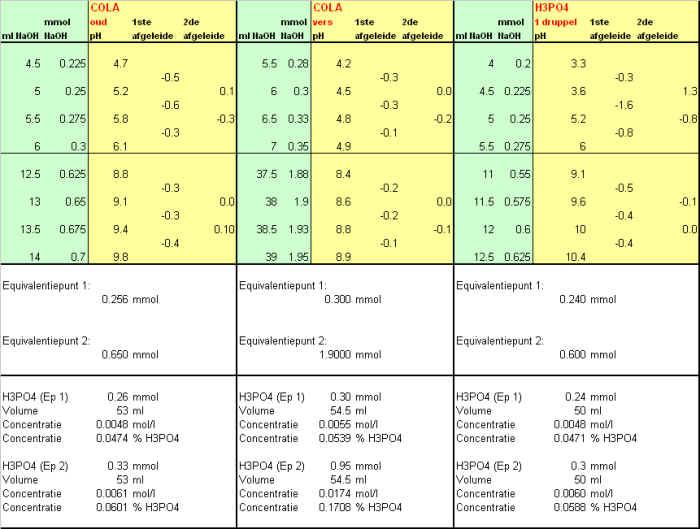
Titratie van fosforzuur: De concentratie van de fosforzuur oplossing die we gemaakt hebben door een druppel 80% fosforzuur aan 50 ml water toe te voegen hebben we hierboven berekend op basis van het equivalentiepunt als zijnde 0.006 mol/l. Er is echter ook nog een andere methode om deze concentratie te bereken nl op basis van de pH. Hierbeneden hebben we de volgende formule afgeleid voor de pH van een fosforzuur oplossing nl:
Dat is een gecompliceerde vergelijking die weliswaar verder vereenvoudigd kan worden maar waar je in deze vorm analytisch gezien niet veel mee kunt. Vroeger was dat ook zo maar m.b.v. excel kunnen we dit soort problemen wel aanpakken. Waar we nu in geÔnteresseerd zijn is de waarde van c aangezien dat de concentratie van fosforzuur is. We weten echter dat de pH van de oplossing 2.6 is, die hebben we gemeten, x is dus bekend. De waardes van de protolyseconstantes K1,K2 en K3 zijn ook bekend. Het makkelijkste is nu om eerst de vergelijking om te werken naar de vorm: A + B + C + y = x. En dit analoog zoals hierbeneden weergegeven op te zetten. Voor c vul je dan in eerste instantie een afschatting in bv. 0.01. Zie in de spreadsheet de worksheet genaamd pH berekeningen. In een cel bereken je het verschil met de berekende x en de gemeten x. Als je nu de solver gebruikt om c te laten variŽren totdat dat verschil 0 is dan wordt er een c berekend die bij de gemeten pH hoort.
Op deze manier bereken we een fosforzuur
concentratie van 0.003 mol/l. |
|
 |
 |
|
c = 0.00336 M in titratievergelijking |
c = 0.0060 M in titratievergelijking |
| De excel-solver methode om de
concentratie te berekenen laat een flinke afwijking zien met de gemeten
curve. De concentratieberekening op basis van het 2de ep laat een betere
overeenkomst zien. Ook dan is het verschil nog relatief groot.
Waarschijnlijk is dit toe te wijzen aan de potentiŽle fouten die
hierboven al benoemd zijn. Ondanks al het hiervoorgaande vindt ik het
verschil tussen theorie en praktijk erg groot. |
|
|
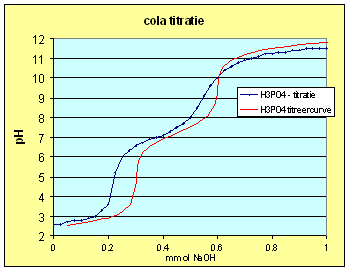
Titratie van oude cola:
Gebruiken we nu de concentratie van fosforzuur zoals we die bepaald hebben in de titratievergelijking en vergelijken de titratiecurve op die manier berekend voor fosforzuur met de voor cola gemeten titratiecurve dan krijgend we de grafiek van hiernaast. We zien onmiddellijk dat de equivalentiepunten afgeplat zijn hetgeen wijst op een sterk bufferende werking.
|
 |
|
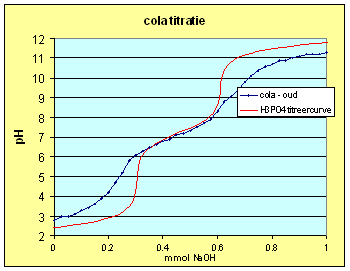
Titratie van verse cola:
Zoals verwacht gaf het titreren van de verse cola een heel ander beeld te zien dan dat van de oude. Dat dit toe te schrijven valt aan de aanwezigheid van CO2 in de cola is zeer aannemelijk aangezien dat de enige component is die met de gehanteerd methode kan ontwijken. Oxidatie van componenten naar zuren door blootstelling aan luchtzuurstof lijkt me niet erg waarschijnlijk voor iets dat je moet drinken. Een aanname die ik echter niet gecontroleerd heb. |
|
| De aanwezigheid
van CO2 betekent dat de elektroneutraliteistvergelijking aangepast moet
worden.Een van de dingen die ik ooit gelezen heb is dat CO2
erin geperst wordt hetgeen betekent dat we in de
elektroneutraliteitsvergelijking geen rekening hoeven te houden met extra
Na+.
Verwerken we een ander en spelen we een beetje met de concentratie van fosforzuur en koolzuur dan kunnen we een titreercurve maken die zeer sterk lijkt op degene die we daadwerkelijk gemeten hebben, vooral in het hoge pH gebied. Concentraties in titreervergelijking: |
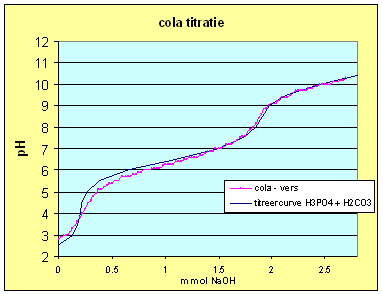 |
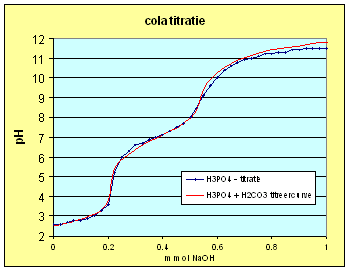
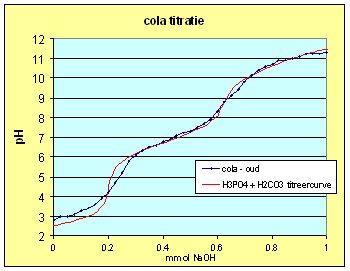
| Passen we dit inzicht toe op de titreercurve van H3PO4 en de oude cola dan krijgen we: | |
 |
 |
| Deze curve is verkregen met
concentraties: C H3PO4 = 0.00420 M C H2CO3 = 0.00230 M Ctot = 0.00650 M |
Deze curve is verkregen met
concentraties: C H3PO4 = 0.00400 C H2CO3 = 0.00450 Ctot = 0.00850 |
| We kunnen dus concluderen dat de H3PO4 titratie zwaar werd beÔnvloed door de aanwezige CO2 in de oplossing. Kijken we naar de cola dan kunnen we het 2de equivalentiepunt ook toekennen aan een mix van fosforzuur en koolzuur. Het 1ste equivalentiepunt krijgen we echter niet zo goed gefit hetgeen er op wijst dat daar een ander zuur ook een bijdrage levert. Dat zou dan echter wel een eenwaardig zuur moeten zijn anders zou de invloed op het 2de equivalentiepunt waarschijnlijk ook waarneembaar zijn. Een vermoeden dat bevestigd wordt als we de andere e-nummer gaan benoemen (zie de tabel hiernaast). | Verklaring E-nummers
voedingszuren: E 330 = Citroenzuur E 331 = Natriumcitraat E 332 = Kaliumcitraat E 333 = Calciumcitraat E 334 = Wijnsteenzuur E 335 = Natriumtartraat E 336 = Kaliumtartraat E 337 = Kaliumnatriumtartraat E 338 = Fosforzuur |
| Waarschijnlijk is citroenzuur de boosdoener. Citroenzuur is echter ook een driewaardig zuur (pK1 =3.128; pK2 = 4.761; pK3 = 6.396) alhoewel de drie pKa's inderdaad in het betreffend gebied vallen. Ik heb een referentie gevonden waarin verteld wordt dat in de door mij gebruikte Cola-Light citroenzuur zit (XLAB-Virtuell). Bovenstaande betekent ook dat alleen het eerste equivalentiepunt bruikbaar is om het zuurgehalte te berekenen, in dit geval een mengsel van fosforzuur en een ander zuur, hoogstwaarschijnlijk citroenzuur. Door deze in de titreercurvevergelijking te stoppen lukt het me echter nog altijd niet om de titreercurves kloppend te krijgen. | |
Conclusie:
|
Opmerkingen:
|
Literatuur:
Relevante websites: |
Achtergrondinformatie:
| De hier uitgevoerde berekeningen zijn gebaseerd op de definitie van zuren, basen en zouten
van Brōnsted
(1923), die de definities van zuren en basen baseerde op het volgende
reactieschema: zuur <=> base + proton (H+-ion) Onder zuren worden stoffen verstaan die protonen kunnen afsplitsen en met basen stoffen die protonen kunnen opnemen. Een verzamelnaam voor zuren en basen is protolyten. Zouten zijn neutrale stoffen die zich in waterige oplossing in ionen splitsen, die zich al of niet als protolyten kunnen gedragen. Kijken we nu naar zoutzuur: HCl --> H+ +
Cl- Sommige stoffen kunnen zich zowel basisch als
zuur gedragen, de amfolyten:
Hetgeen we voor water hebben gedaan kunnen we ook voor zuren en basen doen:
Om nu pH berekeningen te kunnen maken zijn maar een paar vergelijkingen noodzakelijk:
Door deze vergelijkingen uit te schrijven krijgen we evenveel vergelijkingen als onbekenden. Titratie
van fosforzuur met natronloog Gegevens: NaOH =
natronloog
x = [H3O+] pH
berekeningen: De
elektroneutraliteitsvergelijking is het uitgangspunt van de berekeningen. Elke
elektrolytoplossing is in haar geheel elektrisch neutraal. De som van alle
positieve lading is dus gelijk aan de som van alle negatieve lading. Ionen
dragen steeds een geheel aantal elementairladingen en we mogen dus zeggen dat de
som van concentraties van de positieve ionen gelijk is aan de som van de
concentraties van de negatieve ionen, mits men de concentraties van de
meerwaardig geladen ionen met de vereiste factor vermenigvuldigt. Als we H3PO4
oplossen in water dan protolyseert het volgens onderstaande
reactievergelijkingen.
De protolyse
constanten, de water constante de stechiometrische vergelijking en de
elektroneutralitetsvergelijking worden dan:
Uit de
protolyse constanten kunnen we afleiden dat:
Door deze te substitueren in de stechiometrische relatie krijgen we: Voor PO43-:
Voor HPO42-:
Voor H2PO4-:
Substitutie
in de electroneutraliteitsvergelijking geeft:
Deze vergelijking ziet er zeer ingewikkeld uit, maar is te vereenvoudigen (indien we binnen excel solver gebruiken is dat zelfs niet nodig, zie in de spreadsheet de worksheet genaamd pH berekeningen). Omdat voor
fosforzuur K1 >> K2 >> K3 mag
worden geschreven:
Existentiegebieden: We hebben
hierboven de relatie van de verschillende fosfaten met concentratie en pH
afgeleid. Dit maakt het mogelijk om te laten zien bij welke pH welk fosfaat
domineert.
Alleen voor H3PO4
moeten we nog een vergelijking afleiden:
Door nu excel
een tabel aan te maken waar de pH of x in een kolom zetten en bij een
vastgelegde c (bv c=0.1 M) de concentratie van elke species bij een bepaalde pH
uit te rekenen kunnen we onderstaande grafiek maken.
De
titratievergelijking: Dit is een
titratie van een driewaardig zuur met een zeer sterke base.
Bruto
reaktievergelijking: H3PO4 + 3NaOH -> PO4-
+ 3Na+ + 3H2O De PO43- ionen reageren niet verder hetgeen betekent dat de fosfaat concentratie gelijk is aan de fosforzuur concentratie voor we beginnen met titreren. M.a.w.: [PO43-]
= c Onder de
omzettingsgraad l
verstaan we de toegevoegde hoeveelheid reagens in
mol gedeeld door de te bepalen hoeveelheid stof in mol. Voor de titratie van een
eenwaardig zuur met een eenwaardige base ligt het equivalentiepunt bij l=1.
Bij de nu volgende theoretische afleiding van de titratiecurve wordt de aanname
gemaakt dat het volume tijdens de titratie niet verandert.
Dit geef dan de volgende elektroneutraliteitsvergelijking: Oftewel:
Omdat
voor fosforzuur K1 >> K2 >> K3
kunnen we de volgende titratievergelijking formuleren:
Alhoewel we deze vergelijking nog verder kunnen vereenvoudigen om de titratievergelijking in stukjes te knippen en op deze manier uit te rekenen is dat niet nodig. M.b.v. excel is eenvoudig een tabel samen te stellen die de l bij verschillende pH's uitrekent. Uiteraard kan deze tabel weer gebruikt worden om de titratiecurve te tekenen. De titratievergelijking en de concentratie zijn voldoende om onderstaande titratiecurve te berekenen.
Men
ziet in de titreercurve dat bij het derde equivalentiepunt (l=3)in het geheel geen
sprong in de pH meer optreedt. Dit wordt veroorzaakt door de autoprotolyse van
water die bij titraties met zuren met een pKa>10 merkbaar wordt en
de derde equivalentiesprong zo onderdrukt of beter geformuleerd overspoelt. De invloed
van CO2 op de titreercurve: De
aanwezigheid van CO2 laat ons een vrij ingewikkeld plaatje schetsen.
Kijken we in eerste instantie alleen maar naar het CO2 zelf dan
kunnen we de volgende reaktievergelijkingen schetsen: (1) CO2
(g) <=> CO2 (l) (Het evenwicht tussen het opgeloste CO2 en
het CO2 in de lucht Gelukkig
hoeven we met het opstellen van de vergelijkingen geen rekening te houden met
het opgeloste CO2. De pKa
die we in de literatuur vinden voor koolzuur (pKa1 = 6.37) is niet de
echte pKa van koolzuur. In werkelijkheid is het de pKa van
het evenwichtsmengsel van CO2 (l) en koolzuur. Koolzuur zelf is een
veel sterker zuur met een echte pKa1 waarde van 3.58. De
evenwichtsinstelling van de evenwichtsinstelling tussen gas en vloeistof
(reactie 1) laten we buiten beschouwing. Volledig
analoog als voor fosforzuur kunnen we koolzuur ook een
elektroneutraliteistvergelijking opstellen nl:
De
totale elektroneutraliteitsvergelijking voor koolzuur en fosforzuur wordt dan:
We
definiŽren l
nu als:
De
titreercurve-vergelijking wordt dan:
Verder
uitbreiden voor citroenzuur: Citroenzuur is ook een driewaardig zuur (pK1 =3.128; pK2 = 4.761; pK3 = 6.396) waarop we echter niet de vereenvoudiging kunnen toepassen die we bij fosforzuur hebben toegepast. Verder loopt alles precies hetzelfde hetgeen voor de titreervergelijking betekent (H3C=citroenzuur) :
|
24-03-2020
Op 28/2/2006 enkele literatuurreferenties en een opmerking toegevoegd.